
1.알고리즘 '복잡도(complexity)'
복잡도란
- 알고리즘의 성능을 나타내는 척도
- 크게 시간 복잡도, 공간 복잡도로 나눌 수 있다.
1.시간 복잡도
- 특정한 크기의 입력에 대해 알고리즘이 얼마나 오래 걸리는지를 의미한다.
- 알고리즘을 위해 필요한 연산의 횟수
- 복잡도를 표현하기 위해 빅오 표기법을 사용한다.
- 최악의 경우에 대한 연산 횟수가 가장 중요하다.
- N의 범위에 따라 시간 복잡도를 계산하고 사용할 수 있는 알고리즘을 선택하는 방법도 있다.
※ 빅오 표기법 (O, big-O)
빅오란 입력값이 무한대로 향할때 함수의 상한을 설명하는 수학적 표기 방법이다.
- 빅오는 점근적 실행 시간을 표기할 때 가장 널리 쓰이는 수학적 표기 방법이여, 여기서 점근적 실행 시간이란 간단하게 N이라는 입력값이 무한대로 커질때의 실행 시간의 추이를 의미한다.
- 따라서 충분히 큰 입력값에서의 알고리즘의 효율성에 따라 수행 시간이 크게 차이가 날 수 있다.
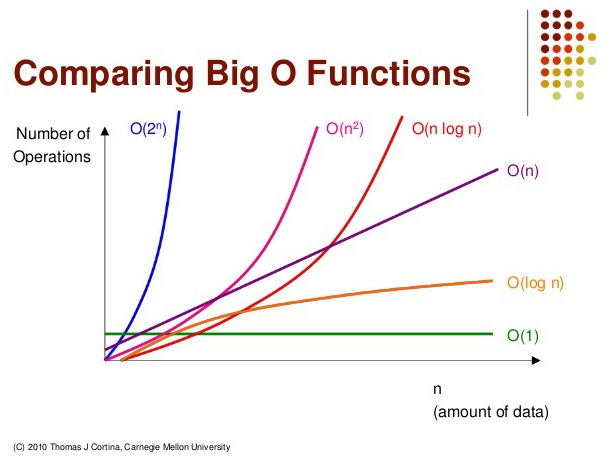
| 빅오 표기법 | 표현 | 설명 |
|---|---|---|
| O(1) | 상수 | 입력값에 상관없이 일정한 실행시간을 최고!의 알고리즘 |
| O(logN) | 로그 | 로그는 매우 큰 입력값에서도 크게 영향을 받지 않는 편이다. |
| O(N) | 선형 | 알고리즘을 수행하는데 걸리는 시간은 입력값에 비례, 모든 입렵값을 적어도 한 번 이상은 살펴봐야 한다. |
| O(NlogN) | 로그 선형 | 병합 정렬등의 대부분 효율이 좋은 알고리즘이 이에 해당, 아무리 좋은 알고리즘이라 할지라도 n log n 보다 빠를 수 없다. |
| O(N^2) | 다항 | 버블 정렬 같은 비효율저긴 정렬 알고리즘이 이에 해당 한다. |
| O(2^N) | 지수 | 피보나치의 수를 재귀로 계산하는 알고리즘이 이에 해당 한다. n^2와 혼동되는 경우가 있는데 2^n이 훨씬 더 크다. |
2.공간 복잡도
- 특정한 크기의 입력에 대해 알고리즘이 얼마나 많은 메모리를 차지하는지를 의미한다.
- 알고리즘을 위해 필요한 메모리의 양
2. P vs NP
1.다항 시간 알고리즘(Polynomial-Time Algorithms)
-
다항 시간(합리적인 시간)안에 풀 수 있는 문제.
-
모든 문제가 다항 시간안에 해결되지 않는다.
- Ex) 튜링의
"Halting Problem(정지 문제)": 정지 문제란
프로그램을 설명한 것과 처음 입력값이 주어졌을 때, 이 프로그램에 입력값을 넣고 실행한다면 이 프로그램이 계산을 끝내고 멈출지 아니면 영원히 계속 계산할지 판정하라.
- 1936년 앨런 튜링이 모든 가능한 입력값에 대해 정지 문제를 풀 수 있는 일반적인 알고리즘은 존재하지 않는다는 것을 증명했다.
- Ex) 튜링의
2.클래스 P
- 다항 시간내에 해결되는 알고리즘을 가지고 있는 결정(decision) 문제의 클래스
- 어떤 상수 k에 대해 O(N^K) 시간에 풀 수 있는 문제
- O(P(N)) - 이때 P(N)은 N상의 다항시간
- 항상 올바른 답을 계산하는 방법
- 다항시간내에 해결되지 않으면 비효율적
3.클래스 NP
- '비결정적인 다항시간' 상에 존재(stand)
- 주로 "추측" or "평행선화(parallelize)"방식으로 계산
- 다항 시간에 "확인할 수 있는" 문제로 구성
- 해의 "후보"가 주어지면 문제 입력 크기에 대한 다항 시간에 그 후보가 올바른 해인지 확인할 수 있음을 의미
- 이 방식의 문제점은 "속도(quickly)"
- 4.P ⊆ NP (아직 증명X)
- NP-complete(완비) 문제는 NP에서 가장 어려운 문제이다.
- 대부분의 전문적인 문제는 P or NP-complete 문제이다.
- NP-complete 문제 : P로 해결 가능하지만 NP로 해결되지 않는 문제(미제문제)
3.여행하는 외판원 문제(Traveling-Salesman-Problem)
1.여행하는 외판원 문제(TSP)
외판원 문제 또는 순회 외판원 문제는 초합 최적화 문제의 일종이다. 이 문제는 NP-난해에 속하며, 흔히
계산 복잡도 이론에서 해를 구하기 어려운 문제의 대표적인 예로 많이 다룬다.
- 외판원은 자신이 사는 도시에서 출발해서 어떤 순서로든 다른 도시를 모두 방문하고 나서 다시 출발점으로 돌아와야 한다.
- 여기서 목표는 각 도시를 정확히 한 번씩(반복 없이) 방문하고,
- 전체 여행한 거리를 최소로 만드는 것이다.
⇒ 그래프 이론의 용어로 엄밀하게 정의한다면,"각 변에 가중치가 주어진 완전 그래프(weighted complete graph)에서 가장 작은 가중치를 가지는 해밀턴 순회를 구하라"라고 표현할 수 있고, 반드시 시작점으로 돌아와야 한다는 제약 조건을 없애도 계산 복잡도는 변하지 않는다.
- 외판원 순회 알고리즘은 무식하게 풀 수 있다. 무조건 0번 도시에서 출발한다고 가정해도 경로의 길이는 다르지 않다.
- 그러면 남은 도시들을 어떤 순서로 방문할지를 정하기만 하면 된다.
- 남은 n-1개의 도시를 나열하는 방법으로는
(n-1)!가지가 있다. - 그래서 재귀 호출을 통해 쉽게 외판원 순회 알고리즘을 설계할 수 있다.
- 그러나 보통 n!의 풀이는 사용하지 않는다. 12!만 해도 479,001,600라는 엄청난 수를 지니기 때문이다.
2.외판원 순회 알고리즘을 더 빠르고 효율적으로 구하는 방법은?
- 모든 정점을 한 번씩 방문하는(출발 정점 제외) 최단 순환 경로를 탐색하는데 최적의 효율로 탐색하기 위해서 사용한다.
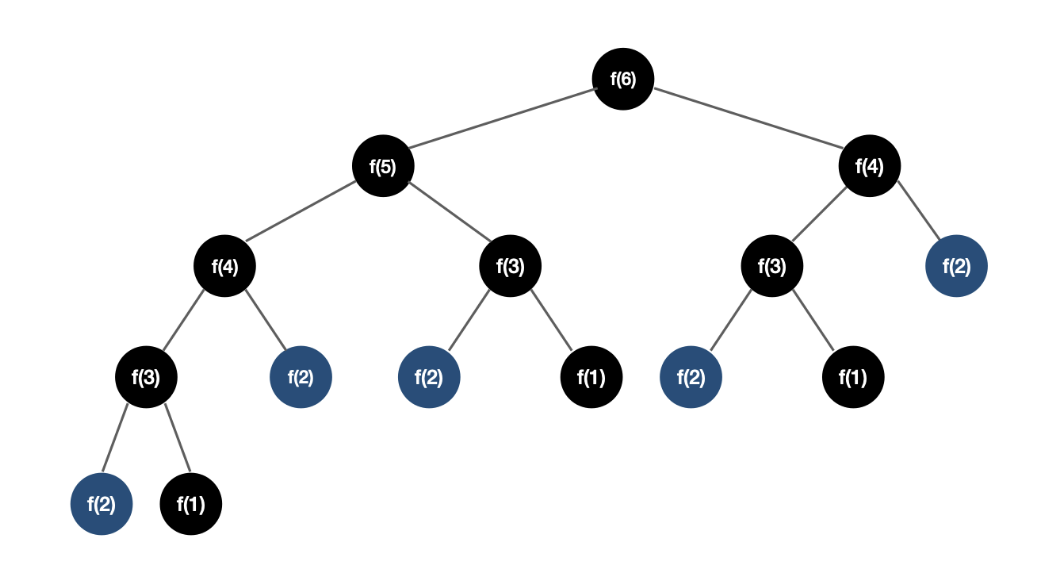
DP 메모제이션
(n-1)!의 모든 경로를 조사하지 않고 중복된 경로를 제거하는 dp 메모제이션 기법을 사용하면 된다.- 동일한 하위 문제의 반복을 막아줌으로써 더 높은 효율로 연산이 이루어지게 해준다. 중복되는 경로의 조사를 제거해주는 것이다.
- 예를 들어, 피보나치 함수는 dp 메모제이션 기법을 통해 O(2^n)의 복잡도를 O(N)까지 줄여준다. **그렇다고 무조건 dp 메모제이션을 적용하면 각 문제의 성질이 다르기 때문에 O(n)으로 줄어든다는 뜻은 아니다.
비트마스킹
- 비트마스킹을 사용하면 bit연산이기 때문에 다른 자료구조(boolean배열)을 사용하는 것보다 훨씬 빠르게 동작되고 코드도 간결해진다.
- 가장 큰 장점은 N이 16개인 경우 2^16가지의 경우를 16bit로 표현이 가능하다.
⇒ 정리하면 TSP(외판원 순회)는 최단 순환 경로를 탐색해야하는데 1) N! 의 중복 경로를 제거해주는 DP 메모제이션 기법을 사용한다. 그래도 2^N의 모든 경우의 수를 표현해야 하기 때문에 그만큼의 공간복잡도가 필요하다. 2) 메모리 사용량도 줄이고 성능 향상을 위해서 2^N의 경우의 수를 Nbit로 표현할 수 있는 비트마스킹으로 사용한다.
⇒ 올라가야 할 계단의 수를 100 개에서 1개로 줄여주는 설계 방법 이라고 보면 된다.
그렇다면 왜 한 정점만 탐색해도 될까?
- DP 메모제이션 기법으로 엄청나게 시간을 단축 할 수 있는 것은 그만큼 중복되는 경로가 많기 때문이다.
- 이 순회 경로는 싸이클로 n개의 정점 중 어느 정점에서 탐색을 시작해도 결과는 똑같다는 것을 알아야 한다.
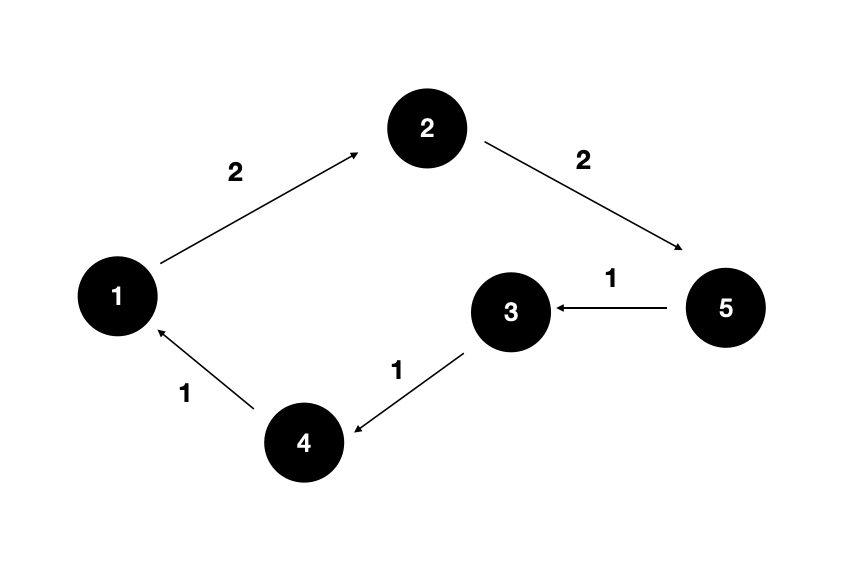
- 어차피 최적 경로 싸이클은 어디서 시작해도 똑같이 나오기 때문에 한 정점에서만 탐색해줘도 된다.
- 1번에서 출발 : 1 → 2 → 5 → 3 → 4 → 1
- 2번에서 출발 : 2 → 5 → 3 → 4 → 1 → 2
- 3번에서 출발 : 3 → 4 → 1 → 2 → 5 → 3
알고리즘 참고 영상(강추) :
[youtube] hungarian dance - sorting algorithms
참고 링크 :
[알고리즘] 복잡도란 무엇인가
빅오 표기법 (O, big-O)
정지 문제
P와 NP
여행하는 외판원 문제(TSP)
