공분산과 상관계수를 알아보자

0. 학습 참고자료

• 파이썬으로 배우는 통계학 교과서

1. 공분산의 정의

2개의 연속형 변수의 관계성을 확인하는 통계량을 공분산이라고 하고 특징은 다음과 같다.

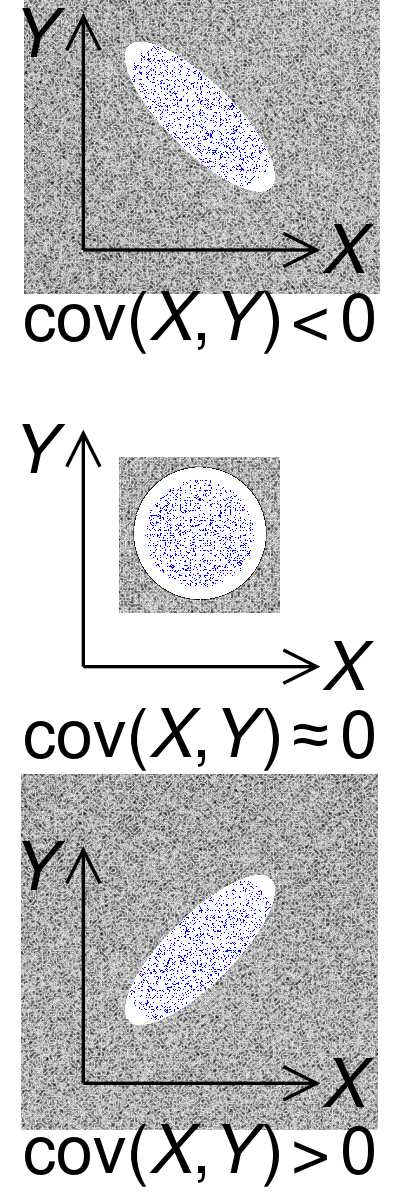
• 공분산이 0보다 클 때: 하나의 변수가 큰 값을 갖게 되면 나머지 변수도 커진다

• 공분산이 0보다 작을 때: 하나의 변수가 큰 값을 갖게 되면 나머지 변수는 작아진다

• 공분산이 0일 때: 두 변수 사이에 관계성이 없다

2. 공분산 계산하기

분산은 편차를 제곱한 값의 평균!

# 이론 구현
def Cov(x, y):
	N = len(x) # 두 변수의 길이는 같을 수밖에 없으니까
    		   # 과소 추정을 방지하기 위해서 N-1로 return을 계산할 수도 있음
    mean_x = np.mean(x) # scipy 등 어떤 라이브러리를 쓰는지에 따라 바꿔야함
    mean_y = np.mean(y)
    
    return sum((x - mean_x) * (y - mean_y))

# scipy를 활용한 구현
import scipy as sp

sp.cov(x, y, ddof=0) # 위에서 len(N)의 경우에 해당
sp.cov(x, y, ddof=1) # 위에서 len(N-1)의 경우에 해당

3. 피어슨 상관계수란?

공분산이 최대값 1에서 최소값 -1사이가 되도록 표준화하는 것

• 공분산 값을 x와 y의 분산의 곱에 제곱근을 씌워 나눠준다
• 일반적으로 그냥 상관계수로 부를 때 피어슨 상관계수를 뜻한다

4. 상관계수와 상관행렬 구하기

import scipy as sp
sp.corrcoef(x, y) # 주대각선이 1, 반 대각선이 상관계수인 행렬이 등장

5. 상관계수가 무의미할 때 확인해봐야 하는 작업

상관계수가 0인 관계를 갖는 변수들이라고 단순하게 값만 보고 판단하면 안된다

그래프를 그려서 어떤 형태를 띄고 있길래 0인지 확인해야 한다