백준 11660[구간 합 구하기 5]

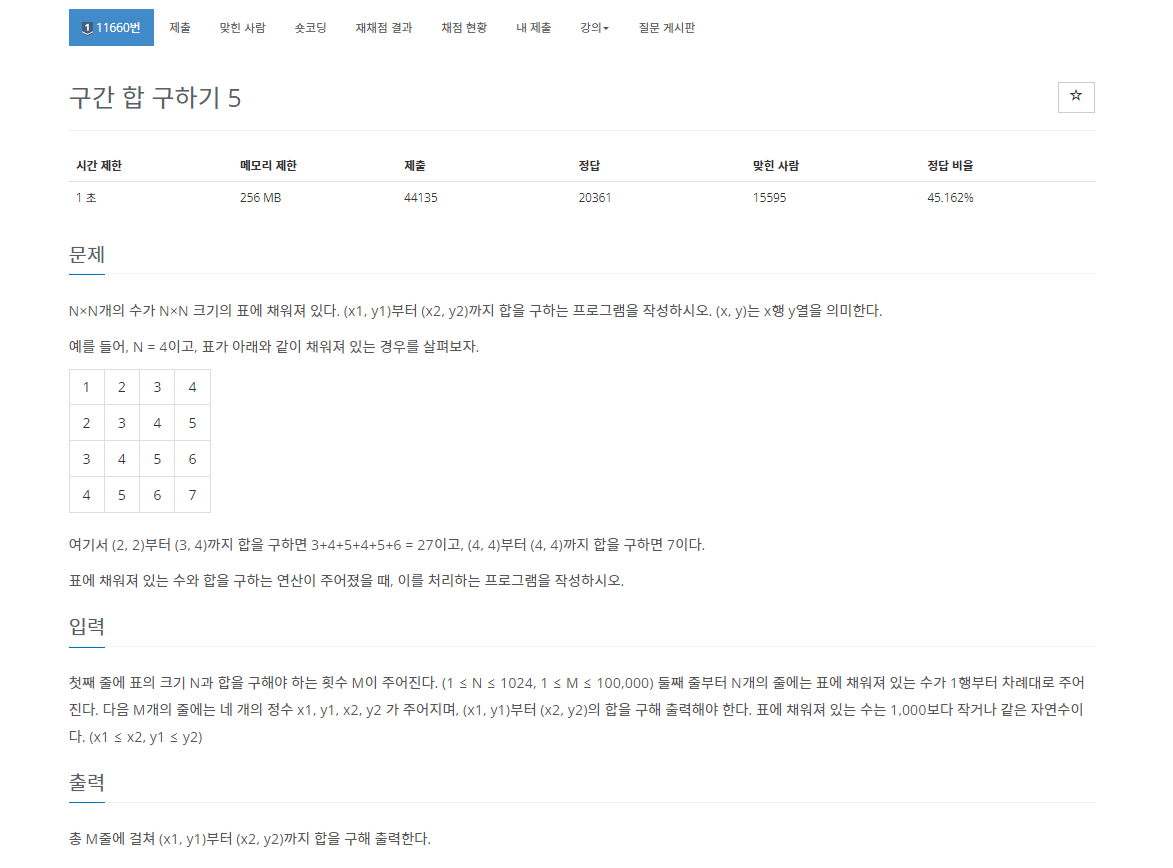
1. 문제 분석 및 접근법

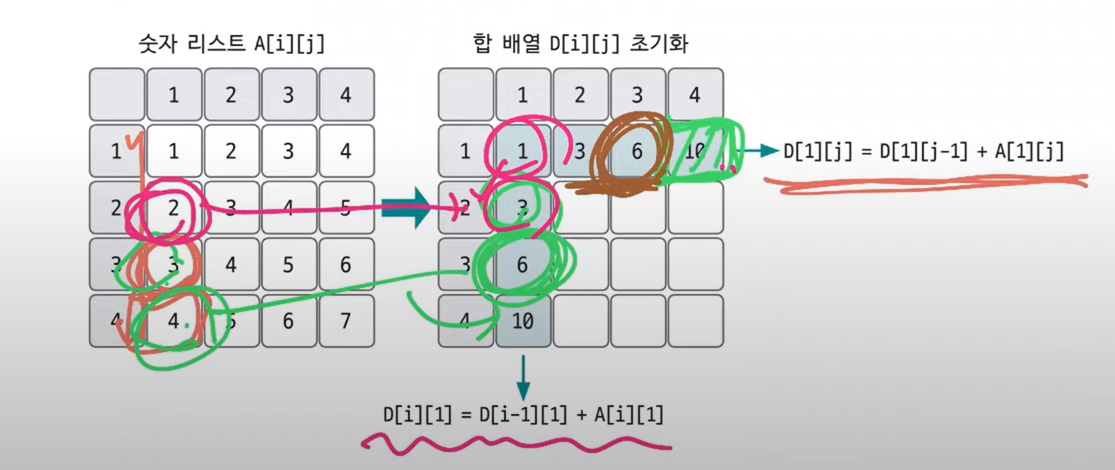
1. 구간 합 배열을 2차원으로 구성하기
   
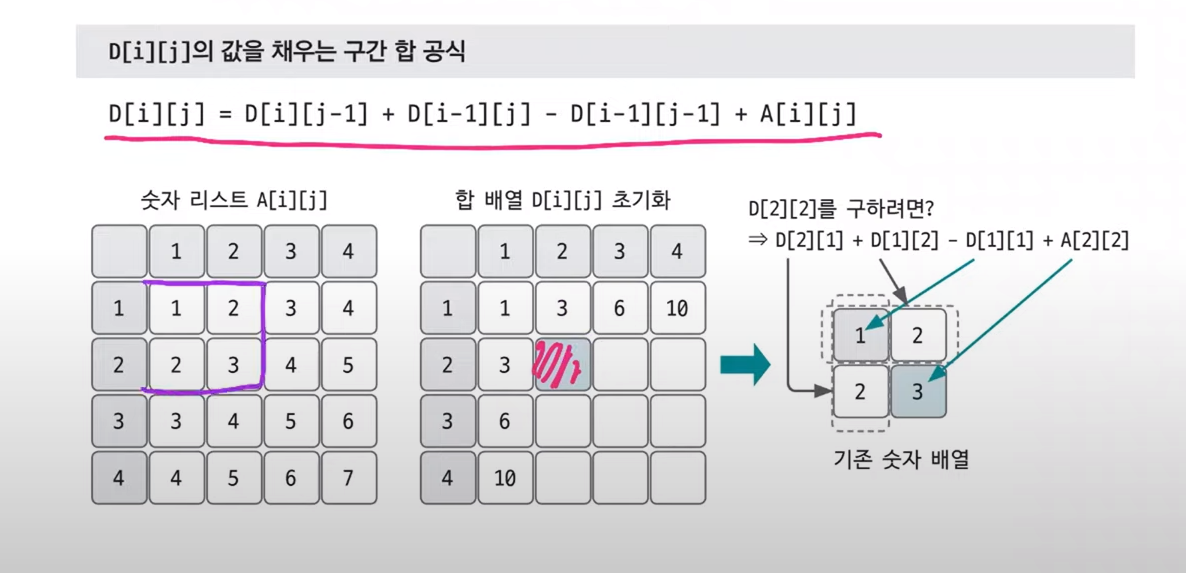
2. 2차원 구간 합 공식
   
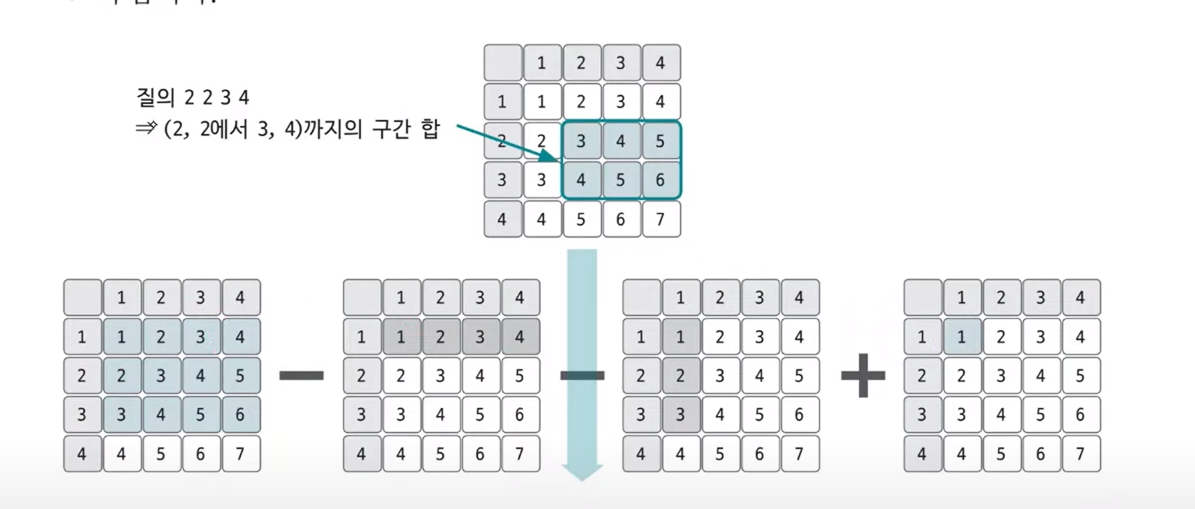
3. x1,x2,y1,y2에 대한 답을 구간 합으로 구하기
   D[x2][y2] - D[x1-1][y2] - D[x2][y1-1] + D[x1-1][Y1-1]

2. 슈도코드 작성

n(리스트 크기) m(질의 수)
A(원본 리스트) D(합 배열)

for n만큼 반복:
	원본 리스트 데이터 저장
    
for 1~n:
	for 1~n:
    	합 배열 저장
        D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]
        
for m만큼 반복:
	D[x2][y2] - D[x1-1][y2] - D[x2][y1-1] + D[x1-1][y1-1] 출력

3. 코드 구현

import sys
input = sys.stdin.readline

n, m = map(int, input().split())
A = [[0] * (n+1)]
D = [[0] * (n+1) for _ in range(n + 1)]

for i in range(n):
   A_row = [0] + [int(x) for x in input().split()]
   A.append(A_row)

for i in range(1, n+1):
   for j in range(1, n+1):
       D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]

for _ in range(m):
   x1, y1, x2, y2 = map(int, input().split())

   result = D[x2][y2] - D[x1-1][y2] - D[x2][y1-1] + D[x1-1][y1-1]

   print(result)