문제 및 예제
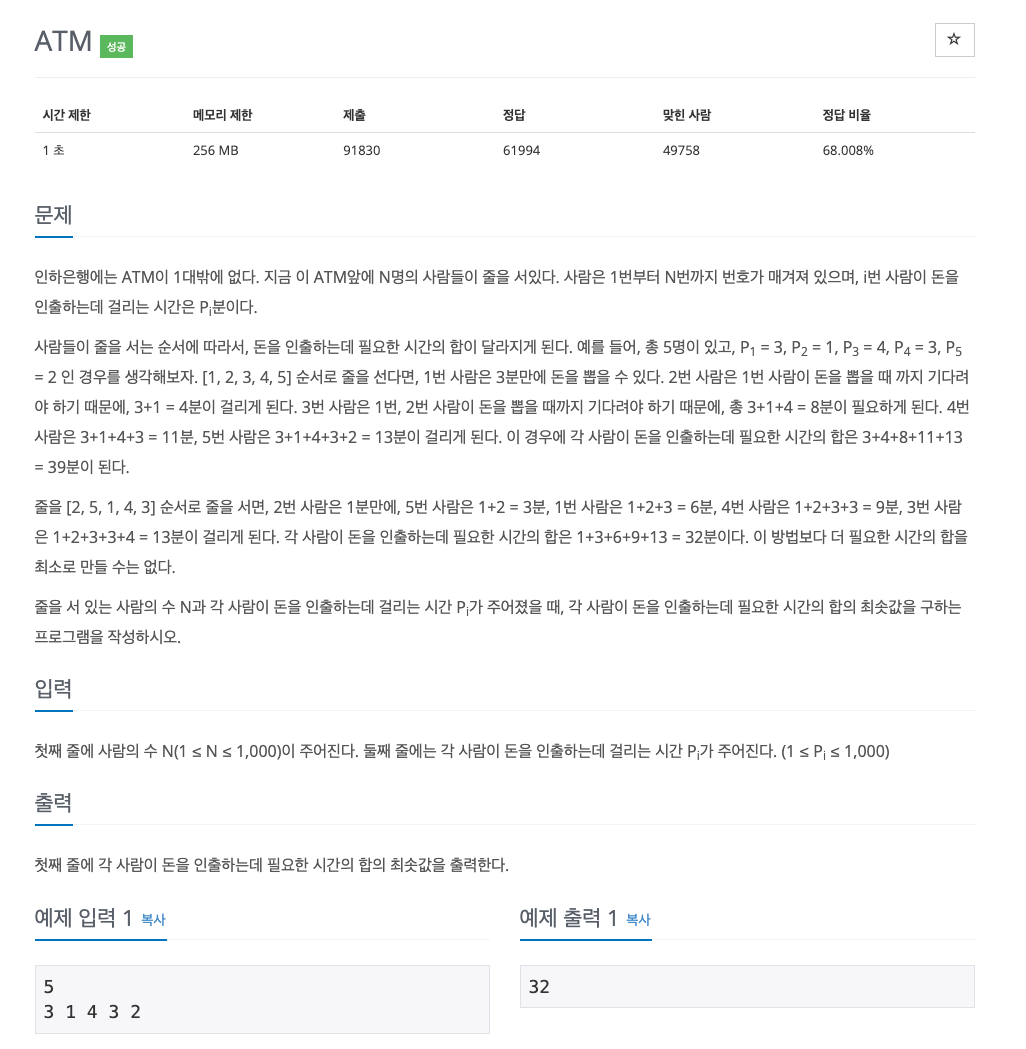
문제 분석
요약하자면, 주어진 데이터를 정렬 후 합 배열을 구하는 문제이다.
최초 접근
정말 단순하게 정렬해주는 내장함수를 써서 리스트를 정렬 후 합배열을 구해서 제출했다. 정답을 맞추긴 했지만, 오늘 공부한 삽입 정렬을 이용해서 다시 풀어봤다. 밑의 코드는 우선 처음에 제출한 코드이다.
import sys
input = sys.stdin.readline
n = int(input())
lst = list(map(int, input().split()))
s_lst = sorted(lst)
result = 0
ans = 0
for i in range(n):
result += s_lst[i]
ans += result
print(ans)삽입 정렬이용
import sys
input = sys.stdin.readline
n = int(input())
lst = list(map(int, input().split()))
s = [0]*n
for i in range(1, n):
insert_point = i # 현재 인덱스 번호 저장
insert_value = lst[i] # 현재 값 저장
for j in range(i-1, -1, -1): # 현재 값 위치의 바로 전 값을 비교하면서 왼쪽으로 이동
if lst[j] < lst[i]: # 비교대상이 나보다 작으면(해당 위치에 삽입해야함)
insert_point = j+1 # 나보다 작은 값의 앞에 저장해야하니 +1
break
if j == 0: # 끝까지 탐색했을 경우(현재 값이 가장 작은 값일 경우)
insert_point = 0 # 맨 앞에 삽입
for j in range(i, insert_point, -1): # i부터 insert_point까지
lst[j] = lst[j-1] # 값들을 오른쪽으로 한 칸씩 shift
lst[insert_point] = insert_value # 삽입 위치에 현재 데이터 저장
s[0] = lst[0]
for i in range(1, n):
s[i] = s[i-1] + lst[i] # 합 배열 공식
sum = 0
for i in range(0, n):
sum += s[i]
print(sum)요약
어려울 건 없는 문제였지만, 포인트는 삽입 정렬과 합 배열이다.
삽입정렬은 따로 글로 정리해놨으니, 간단하게 합 배열 공식만 적어놓겠다.
s[0] = lst[0]
for i in range(1, n):
s[i] = s[i-1] + lst[i] # 합 배열 공식s[0] = lst[0]합 배열의 첫 번째 값에 원래 배열의 첫 번째 값 저장for i in range(1, n):합 배열의 첫 번째 값은 다른 값을 더할 필요가 없기 때문에 인덱스 번호1부터 loop 시작s[i] = s[i-1] + lst[i]이전 합 배열 값에 원래 배열의 현재 값 더해서 저장
