🎄 트리
📎 그래프 (Graph)
💡 그래프 : 노드(node)와 노드 사이에 연결된 간선(edge)의 정보를 가지고 있는 자료구조

- ‘서로 다른 개체가 연결되어 있다 → 그래프 알고리즘 고려
- ex) 여러개의 도시가 연결되어 있다.
📎 트리 (Tree)
💡 트리 : 두 개의 노드 사이에 반드시 1개의 경로만을 가지며 사이클이 존재하지 않는 방향 그래프이다.
- 트리는 그래프 중에서도 특수한 케이스에 해당하는 자료 구조이다.

-
방향 그래프
-
계층적 구조 (부모-자식 관계)
-
사이클, 자체 간선 (self-loop)가 불가능
-
모든 자식 노드는 하나의 부모 노드를 가지며, 따라서 루트 노드는 하나만 존재
→ 노드가 N개인 트리는 항상 N-1개의 간선을 가짐
-
임의의 두 노드 간의 경로는 유일
📌 트리 종류
○ 편향 트리 (skew tree)
- 모든 노드들이 자식을 하나만 가진 트리
- 왼쪽 방향으로 자식을 하나만 가지면 left skew tree, 오른쪽으로 가지면 right skew tree라고 한다.

○ 이진 트리 (Binary Tree)
- 각 노드의 차수 (자식 노드)가 2 이하인 트리

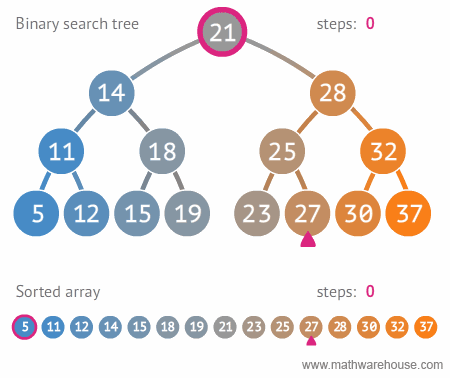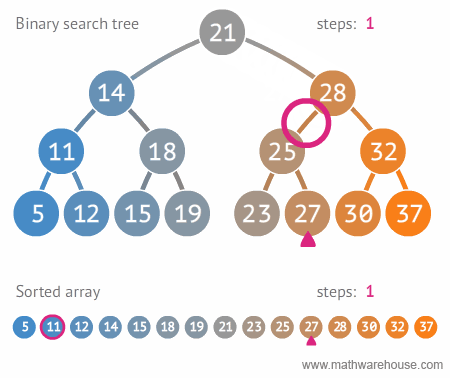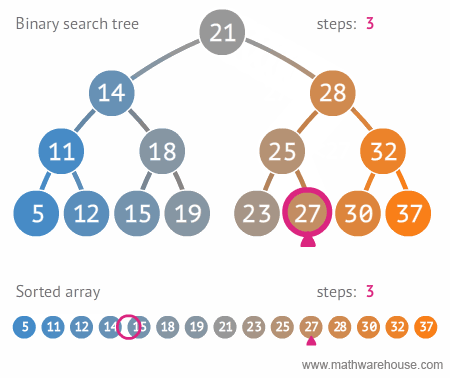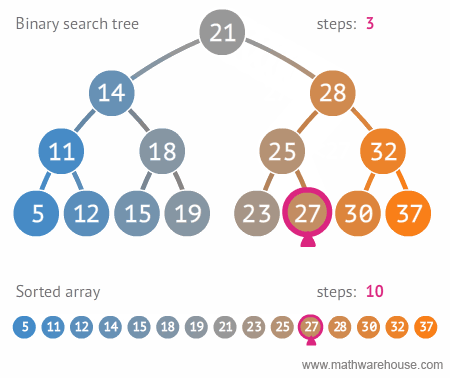
○ 이진 탐색 트리 (Binary Search Tree, BST)
- 순서화된 이진 트리 : 자식 노드가 2개 이하
- 탐색에 최적화된 이진 트리, 하지만 재구성 할 때 트리 구조를 만들고 유지할 때 오버헤드가 크다.
- 노드의 왼쪽 자식은 부모의 값보다 작은 값을 가지며, 오른쪽 자식은 부모보다 큰 값을 가진다. (왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드)
- 중위 순회로 정렬된 순서를 읽을 수 있다.
○ m원 탐색 트리 (M-way Search Tree)
-
최대 m개의 서브 트리를 갖는 탐색 트리
-
이진 탐색 트리의 확장된 형태로 높이를 줄이기 위해 사용

-
다원 탐색 트리는 스스로 균형을 유지하기 못하기 때문에 불균형이 발생할 수 있으며, 이 경우 검색 성능이 떨어지게 된다.

- 이를 보완하기 위해 스스로 균형을 유지하는
Balanced Tree가 있다.
○ 균형 트리 (B-Tree, Balanced Tree)
- m원 탐색 트리에서 높이 균형을 유지하는 트리
- 노드의 key의 수가 k개라면, 자식 node의 수는 k+1개이다.
- 루트와 잎 노드를 제외한 트리의 각 노드는 최소 m/2보다 크거나 같은 정수의 서브트리를 갖는다.
- 트리의 루트는 최소 2개의 서브트리를 갖는다.
- 트리의 모든 잎 노드는 같은 레벨에 있다.
- B+ tree, B* tree도 있다. (참고)

○ AVL 트리 (Adelson-Velsky and Landis tree)
- 자가 균형 이진 탐색 트리, 스스로 균형을 잡는 데이터 구조이다.
- 이진탐색트리는 한쪽으로 노드가 쏠릴 수 있다. 최악의 경우 O(N)의 시간이 필요하다.
-> 이런 단점을 극복할 수 있는 자료구조가 AVL 트리이다.
- 이진 탐색 트리의 속성을 가진다.
- 왼쪽, 오른쪽 서브 트리의 높이 차이가 최대 1이다.
- 높이 차이가 1보다 커지면 회전 (rotation)을 균형을 맞춰 높이 차이를 줄인다.
- 삽입, 검색, 삭제의 시간 복잡도가 O(logN)이다. (N : 노드의 개수)
- 균형이 무너졌는지 판단할 때 Balance Factor를 사용한다.
- 참고
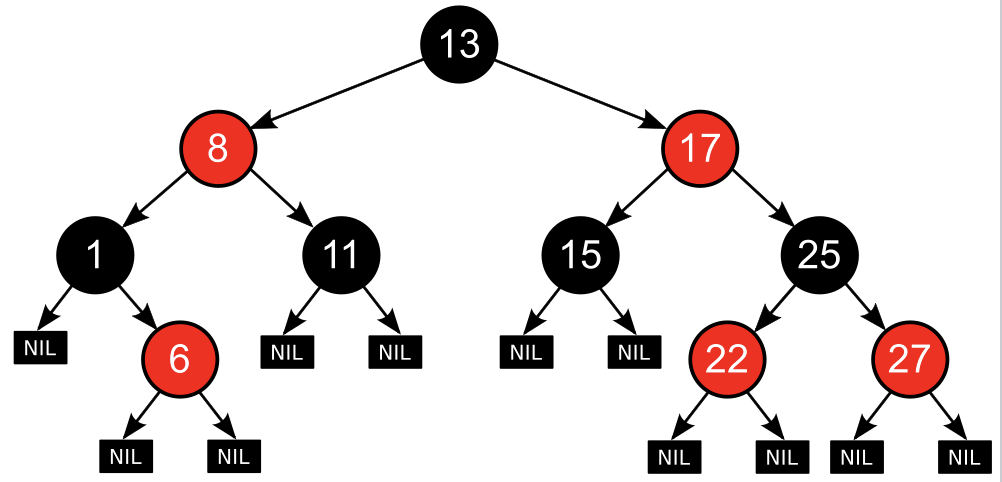
○ Red-Black Tree
- 레드-블랙 트리는 자가 균형 이진 탐색트리이다.
- 자료의 삽입과 삭제, 검색에서 최악의 경우에도 일정한 실행 시간을 보장한다(worst-case guarantees).
- 모든 노드는 빨간색 혹은 검은색이다.
- 루트 노드는 검은색이다.
- 모든 리프 노드 (NIL)들은 검은색이다. (NIL: null leaf, 자료를 갖지 않고 트리의 끝을 나타내는 노드)
- 빨간색 노드의 자식은 검은색이다.
== No double red (빨간색 노드가 연속으로 나올 수 없다.) - 모든 리프 노드에서 Black Depth는 같다.
== 리프노드에서 루트 노드까지 가는 경로에서 만나는 검은색 노드의 개수가 같다.
- 사용 예
- Java 8 이후, HashMap의 Seperate Chaining에서 LinkedList 대신 RB tree를 사용한다. (O(N) -> O(logN))
- Collection에서 ArrayList의 내부적인 알고리즘이 RBT로 이루어져 있다.
- C++의 map의 내부 구현은 검색, 삽입, 삭제가 O(logN)으로 동작하는 RB 트리로 되어있다.
○ AVL tree vs Red-Black tree
1) AVL tree
- 조회 시 더 빠르다.
- 노드에 색깔이 없다.
- 단점 : Balance factor나 height를 노드에 저장하기 때문에 각 노드 당 integer 값을 하나 저장하고 있어야 한다.
2) Red-Black tree
- 삽입, 삭제 작업 시 균형을 맞추기 위한 작업 횟수가 적다.
RB : O(1), AVL : O(logN) - 각 노드 당 색깔을 표현하는데 1bit만 필요하다.
📌 트리의 적용
1️⃣ Spanning trees (신장 트리)
-
그래프 내의 모든 정점을 포함하는 트리 구조
-
최소의 간선을 이용하여 모든 노드를 연결하고자 하는 경우
→ N개의 노드를 (N-1)개의 간선으로 연결
-
예) 통신 네트워크, 라우터에서 사용되는 최단 경로

2️⃣ 이진 탐색 트리
- 데이터를 정렬된 상태로 유지하는데 도움이 된다.
3️⃣ 계층적 구조 데이터
- 트리는 데이터를 계층 구조로 저장한다.
- 예) 폴더와 파일
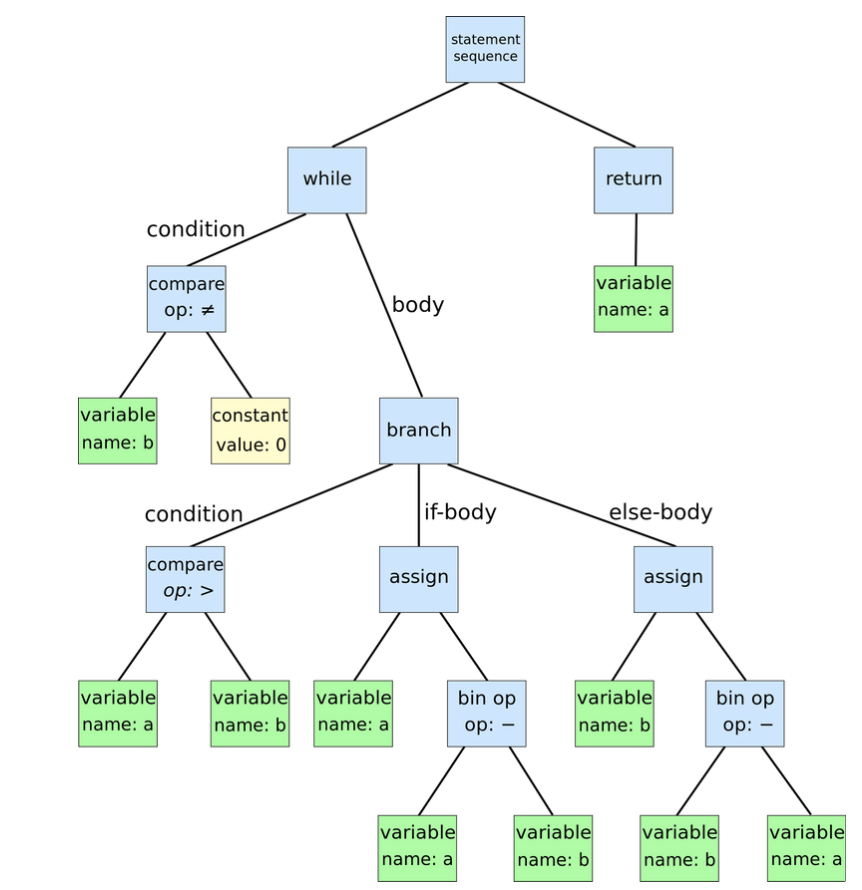
4️⃣ Syntax tree
- 구문 트리는 컴파일러에서 사용되는 프로그램 소스 코드의 구조를 나타낸다.
- 컴파일러는 계층 구조로 된 정보를 추출하여 Syntax Tree로 만든다.
5️⃣ Trie
- 문자열을 빠르게 탐색할 수 있는 자료구조이다.

6️⃣ Heap
- priority queue을 구현하는데 사용될 수 있다.
- 배열 형태로 표현할 수 있는 트리 데이터 구조이다.
- 예) 최소 힙은 항상 부모 노드가 자식 노드보다 크기가 작은 자료구조로 집합에서 가장 작은 수만을 꺼내올 때 유용한 자료구조이다.
7️⃣ DB indexing
- 데이터 베이스 인덱싱을 구현하는데 트리를 사용한다.
- 예) B-Tree, B+ Tree, AVL Tree
📌 트리 구조 장점
- 효율적인 삽입, 삭제, 검색이 가능
- 계층적인 구조를 가진다.
- List, LinkedList보다 적은 메모리 공간을 사용한다.
📌 트리 구조 단점
- 포인터를 위한 추가 메모리가 필요하다.
- 다른 데이터 구조에 비해 확장성이 제한된다.
- 대용량 데이터에는 적합하지 않다.
- 불균형이 심해지면 성능이 저하되고, 효율성이 떨어진다.
📌 트리의 순회
트리의 모든 노드들을 방문하는 과정을 트리 순회 (Treee Traversal)이라고 한다.
전위 순회 (Pre-order), 중위 순회 (In-order), 후위 순회 (Post-order) 세 가지가 있으며, 보통 재귀로 구현된다.
○ 전위 순회 (Pre-order)
전위 순회는 깊이 우선 순회 (Depth-First Traversal)이라고도 한다.
트리를 복사하거나, 전위 표기법을 구하는데 주로 사용된다. 트리를 복사할 때 전위 순회를 사용하는 이유는 트리를 생성할 때 자식 노드보다 부모 노드가 먼저 생성되어야 하기 때문이다.
- root 노드를 방문한다.
- 왼쪽 서브 트리를 전위 순회한다.
- 오른쪽 서브 트리를 전위 순회 한다.
 `A → B → D → E → C → F → G`
`A → B → D → E → C → F → G`
○ 중위 순회 (In-order)
중위 순회는 왼쪽 오른쪽 대칭으로 순회하기 때문에 대칭 순회 (Symmetric traversal)이라고도 한다.
이진 탐색 트리에서 오른차순 또는 내림차순으로 값을 가져올 때 사용한다.
- 왼쪽 서브 트리를 중위 순회한다.
- root 노드를 방문한다.
- 오른쪽 서브 트리를 중위 순회한다.
 `D → B → E → A → F → C → G`
`D → B → E → A → F → C → G`
○ 후위 순회 (Post-order)
후위 순회는 주로 트리를 삭제하는데 사용된다.
이유는 부모노드를 삭제하기 전에 자식 노드를 삭제하는 순으로 노드를 삭제해야 하기 때문이다.
- 왼쪽 서브트리를 후위 순회한다.
- 오른쪽 서브트리를 후위 순회한다.
- root노드를 방문한다.
 `D → E → B → F → G → C → A`
`D → E → B → F → G → C → A`
참고
https://www.geeksforgeeks.org/introduction-to-tree-data-structure-and-algorithm-tutorials/
https://yoongrammer.tistory.com/68
https://laboputer.github.io/ps/2017/09/29/graph/
https://hayden-archive.tistory.com/392
예상 질문
- 트리 자료 구조에 대해 설명해주세요.
- 트리의 종류에 대해 설명해주세요.
- 트리를 사용하는 예와 쓰는 이유에 대해 설명해주세요.
- 이진 탐색 트리에 대해 설명해주세요.
