⭐️ 이 포스트는 편한 말투를 사용한다. 영어 용어를 읽히는대로 한국어로 쓰기도 한다. 긴 용어는 줄여서 표현을 하기도 한다. 오타가 있을 수 있다.
📖 이 포스트는 Tim Roughgarden 교수의 Algorithms Illuminated 를 공부하며 정리한 것이다. 책의 챕터 번호를 따른다.
한 줄 소개: 허프만 코드는 데이터를 compression(압축) 하는 코드다.
14.1. Codes
1. Fixed Length Binary Codes
우리가 fixed length binary code 로 어떤 정보를 표현한다고 하자. 예를 들어 알파벳을 표현한다면, 대문자, 소문자, 부호 등 포함해서 64개의 심볼이 있다고 하고, 그려면 64개를 비트의 나열(바이네리 스트링)로 표현하려면 2^6 = 64 니까 6비트가 필요하겠다. 이게 대략 아스키 코드가 작동하는 방식이다. Fixed-length 코드가 자연스럽고 쉬운 방식이긴 하다. 하지만 알고리즘에서 항상 해야되는 질문이 있다.
Can we do better? (더 좋은 방법은 없을까?)
2. Variable Length Codes
고정된 길이를 생각해봤으니 이제는 변화 가능한 길이를 생각해보자. 어떤 알파벳은 다른 알파벳보다 많이 등장할 수 있고, 이럴때는 variable-length (줄여서 vl 이라고 하겠다) 코드가 픽스드 보다 좋다. vl이 더 복잡하긴 하다. 예를 들어, a,b,c,d 가 있다. 픽스드라면 우리는 순서대로 00,01,10,11로 표현할 수 있다. 버라이어블이라면 일부는 1-비트로 인코딩할 수 있으니 0, 01, 10, 1 로 표현할 수 있다.
여기서 퀴즈: 그럼 vl로 001은 뭔가?
1. ab
2. cd
3. aad
4. 정보가 충분하지 않음
답: 4. 정보가 충분하지 않다. 어디서 끊기는지 알 수 없다. 0, 01? 0,0,1 ?
따라서 vl에 충분한 정보가 더해지지 않으면 모호하다. 픽스드에서는 길이가 정해져 있으니 어디서 끊기는지 걱정할 필요가 없다. 예를 들어, 6비트로 고정해서 표현한다면, 7번째 비트에서 두 번째 심볼이 나온다는 걸 안다. 따라서 버라이어블을 쓰려면 constraint를 줘야 한다.
그래서 어떤 조건을 더해서 버라이어블의 모호함을 없앨 건가?
3. Prefix-Free Codes
프리픽스 프리하게 만들어주면, ambiguity를 없앨 수 있다. 프리픽스 프리가 뭔소리냐면 예를 들어 a,b 심볼을 인코딩할때, a가 b의 프리픽스가 될 수 없고, b가 a의 프리픽스가 될 수 없다는 소리다. (a,b가 0, 01이라면 a는 b의 프리픽스다, 0, 10이라면 어떤 것도 서로의 프리픽스가 될 수 없다.) 예로 첫 5비트가 a라면, 프리픽스 프리 코드에서는 이 첫 5비트가 다른 심볼의 프리픽스가 될 수 없기때문에 a라고 확신할 수 있다.
프리픽스 프리인 픽스드 랭스가 아닌 예시. a,b,c,d 가 있다면, 0, 10, 11, 111 이렇게 된다. 0을 a를 인코딩하기 위해 썼기 때문에 다른 심볼을 인코딩할때 0으로 시작하는 애가 있으면 안된다. 따라서 나머지는 다 1로 시작해야 된다. 10을 b에 썼기 때문에 나머지는 11로 시작해야된다. 11을 c에 썼으니 나머지는 111로 시작해야 된다.
4. Prefix-Free Codes의 장점
버라이어블 랭스이고 프리픽스 프리인 코드는 각 심볼의 등장 빈도가 다를때 픽스드 랭스보다 좋다. 예를 들어, 우리가 과거 어떤 문서를 인코딩해본 경험으로 심볼들의 빈도가 다음과 같다고 해보자.
a: 60%, b: 25%, c: 10%, d: 5%.
그럼 이제 픽스드 랭스랑 퍼포먼스를 비교해보자. a, b, c, d 순서대로, 픽스드는 앞선 예시와 동일하게 00, 01, 10, 11, 버라이블 랭스 프리픽스 프리는 0, 10, 11, 111 이다.
여기서 퍼포먼스라 함은 한 심볼당 평균적으로 얼마나 많은 비트가 쓰였는지를 보는 거다. uniform distribution 이라면 (빈도가 모두 동일한 경우라면) 픽스드 랭스의 승이다. 하지만 빈도가 다를 경우는 weighted average를 계산해야하니 결과가 달라진다. 픽스드는 당연히 심볼 당 2비트다. 프리픽스 프리는 1*0.6 + 2*0.25 + 3*0.1 + 3*0.05 = 1.55. 즉, 심볼 당 1.55비트다. 반대로 빈도가 역순이었다고 생각해보자. 그러면 3*0.6 + 3*0.25 + 2*0.1 + 1*0.05 = 2.8. 픽스드보다 안좋아진다.
결론: 심볼 프리퀀시에 따라 각 심볼의 best binary code 를 뭘로 해야할지 달라진다.
5. 문제 정의
이제 우리는 명확하게 무엇이 문제인지 무엇을 풀어야할지 알게 되었다. 심볼의 빈도에 따라서 어떤 프리픽스 프리 코드를 해야할지 찾는 거다. (문제는 항상 인풋과 원하는 아웃풋으로 나뉜다)
Problem: Optimal Prefix-Free Codes
Input:
A nonnegative frequency for each symbol of an alphabet of size
Ouput:
A prefix-free binary code with the minimum-possible average encoding length:
* (number of bits used to encode a).
간단히 말해서 각 심볼당 빈도가 주어지면, 심볼당 평균 인코딩 랭스가 제일 짧아지는 경우를 찾으면 된다.
근데 심볼 빈도는 어떻게 알 수 있나? 어떤 경우는 도메인 지식으로 알 수 있다 (예. 사람 DNA에 각 뉴클리오베이스의 빈도). MP3 파일을 인코딩하는 경우에는, 인코더가 initial digital 버전을 만들때 심볼 프리퀀시를 계산해두고 압축할 때 사용한다.
문제는 최적의 경우를 찾기 위해서 확인할 케이스가 너무 많아 보인다는 것이다. 알파벳 사이즈에 따라 확인할 코드 수가 exponentially 자라기 때문이다 (예를 들어, 알파벳 사이즈가 n이면 n! 경우가 있을 것이다). 하지만 다행이도 깔쌈한 greedy algorithm 으로 이 문제를 해결할 수 있다.
14.2 Codes as Trees
어떻게 n개의 코드가 서로 프리픽스 프리임을 보장할 수 있을까? 이때 우리는 바이내리 트리를 사용한다. 세 가지 예시를 보면서 코드랑 트리가 어떻게 연관되고 트리를 사용하는 게 어떤 도움을 줄 수 있는지 이해해보자.
1. Three Examples
먼저 픽스드 랭스를 트리로 표현해보자. 예시는 전과 같이 a, b, c, d 가 순서대로 00, 01, 10, 11로 인코딩. 트리로 표현하면 다음과 같다. 부모 노드와 자식 노드들을 잇는 엣지는 0 또는 1로 라벨링된다. 그리고 알맞게 노드에 심볼을 라벨링한다.
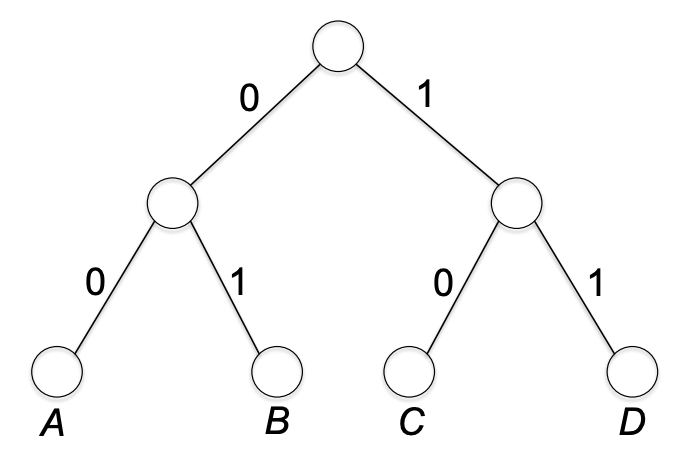
루트에서 두 엣지를 traverse 하면 path가 정해진다. 그리고 이 두 엣지를 심볼의 인코딩이라고 해석하면 된다.
이제 버라이어블 랭스 코드 예시를 보자 (논프리픽스 프리 버전). a, b, c, d가 0, 01, 10, 1. 트리로는 다음과 같다.

a, d가 각각 b, c의 프리픽스라 a, d를 거쳐서 b, c가 되는 것을 확인할 수 있다.
마지막으로 프리픽스 프리 버라이어블 랭스 코드를 보자. a, b, c, d가 0, 10, 110, 111.
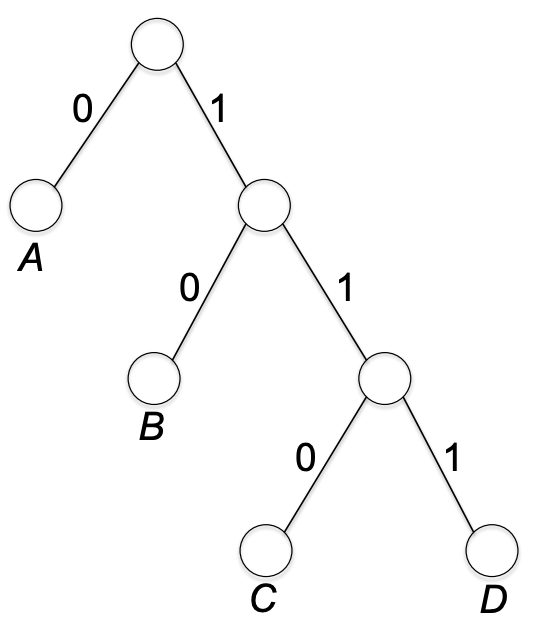
이렇게 어떤 바이내리 코드라도 left edge, right edge가 각각 0과 1로 labeled된 바이내리 트리로 표현할 수 있다. 패스의 엣지 수는 해당 심볼의 비트 수와 같다. 따라서 우리는 다음과 같은 proposition(명제)을 갖는다.
Proposition 14.1 (encoding length and node depth)
모든 바이너리 코드에 대하여, 어떤 심볼의 인코딩 길이는 해당 트리에 라벨이 그 심볼인 노드의 깊이와 같다.
2. 그래서 어떻게 생긴 트리가 Prefix-Free Codes를 표현하나?
앞서서 바이너리 트리로 (픽스드든 아니든 프리픽스 프리든 아니든) 어떤 바이너리 코드든지 표현할 수 있음을 확인했다. 그런지 첫 번째와 세 번째 트리에서 보았듯, 둘 다 프리픽스 프리이지만 모양이 다르다. 하지만 이 둘은 두 번째 (프리픽스 프리가 아닌) 트리와 다른 둘 만의 공통점을 가지고 있다; 바로 리프 노드에만 심볼이 라벨링되어있다는 것이다.
일반화해서 말하자면, 심볼 a가 심볼 b의 프리픽스일려면, a 노드가 b 노드의 ancestor 여야만 한다 (if and only if). 반면에 리프 노드는 그 어떤 노드의 ancestor도 될 수가 없으니, 리프 노드에만 라벨링이 된 경우, 우리는 그 트리가 프리픽스 프리 코드를 나타냄을 알 수 있다. 프리픽스 프리 코드 트리에서 디코딩은 다음과 같이 간단하다.

3. 문제 재정의하기
이제 우리는 최적화된 프리픽스 프리 코드 찾기 문제를 오직 바이너리 트리만을 이용해서 아주 간단하게 표현할 수 있다. 여기서 는 의 심볼과 리프가 일대일 대응되는 바이너리 트리를 의미한다. 리프와 일대일 대응이므로 는 프리픽스 프리 코드가 된다.
Problem: Optimal Prefix-Free Codes (Rephrased)
Input:
A nonnegative frequency for each symbol of an alphabet of size
Ouput:
A with the minimum-possible average leaf depth.
와 심볼 프리퀀시 에 대하여 트리의 심볼의 빈도가 고려된 평균 리프까지 깊이 (즉 한 심볼당 평균 비트 수)를 다음과 같이 표현하자.
따라서 우리는 이 최소화되는 를 찾으면 되겠다.
14.3 Huffman's Greedy Algorithm
1. Building Trees Through Successive Mergers
허프만의 아이디어는 Bottom-up 방식이다.여기서 바텀업 방식은 리프 노드 n개(즉, 심볼 n개)에서 시작해서 트리의 루트까지 올라가는 방식인데, 올라갈때 연속적인 머징을 통해서 트리를 만든다. 간단한 예시를 보자. 이고 리프 노드부터 시작한다.
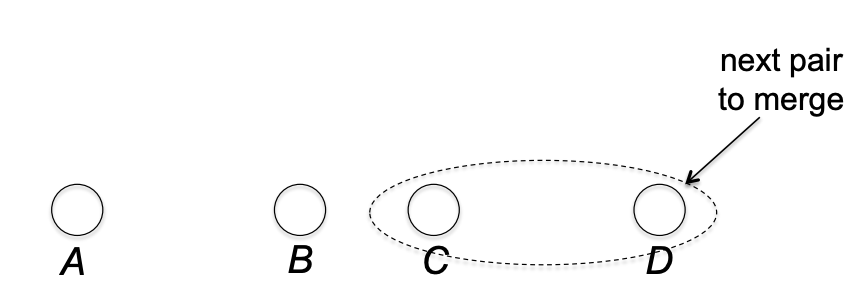
먼저 C, D를 묶는다. C, D는 sibiling 이 된다.
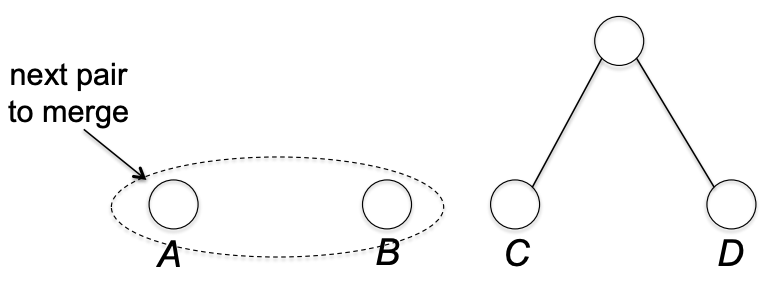
다음으로 A, B를 묶는다. A, B는 sibiling 이 된다.
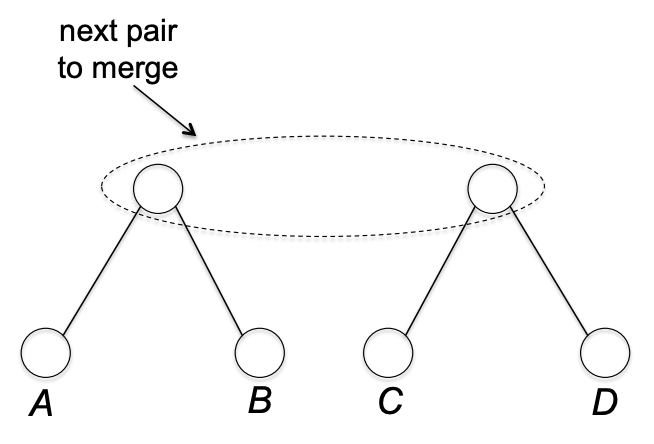
다음으로 위에 두 노드를 묶는다.
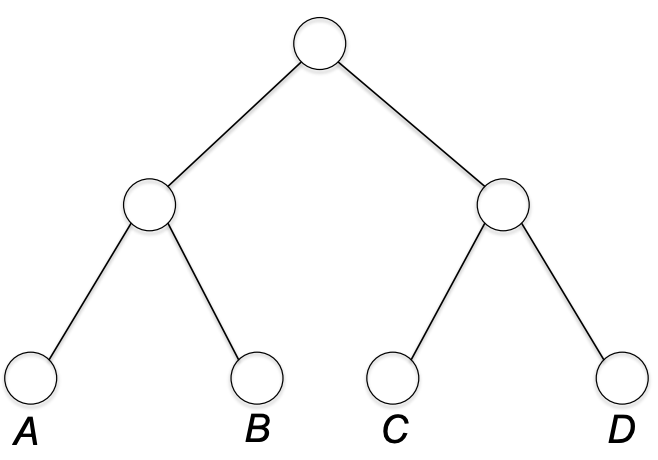
그럼 완성. 위 트리는 14.2.1의 픽스드 랭스 코드를 표현하게 된다. 다른 방식으로 묶을 수도 있다.
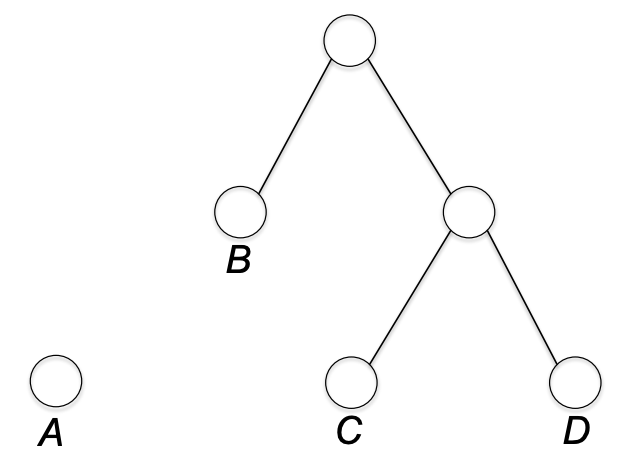
C,D를 묶은 다음 B와 위 노드를 묶는다.
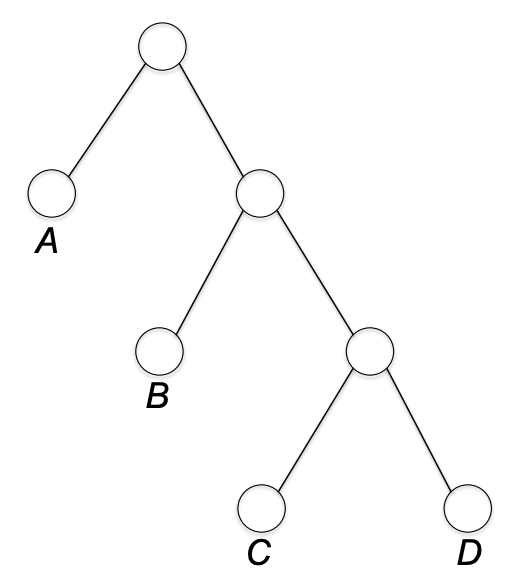
마지막으로 A 노드를 제일 위 노드와 묶는다. 그럼 이는 프리픽스 프리 버라이어블 랭스 코드를 표현하게 된다.
이처럼 허프만의 그리디 알고리즘은 일반적으로 forest(binary tree의 collection)를 형성한다. 그리고 이 숲에서 각 iteration 마다 두 개의 트리를 고르고, 두 트리의 루트를 각각 left and right children 으로 하여 묶는다. 그리고 단 하나의 트리가 남을 때까지 반복하고 멈춘다.
퀴즈: 허프만의 그리디 알고리즘은 멈추기 전까지 몇 번의 merger를 하는가? ( 라고 하자.)
1. n-1
2. n
3. (n+1)n/2
4. 정보가 충분하지 않다.
답은 1. n-1. n개의 트리에서 시작해서 1개의 트리가 될때까지, n-1번의 머징을 하게 된다.
2. Huffman's Greedy Criterion
앞서서는 그냥 머징을 해봤다면, 이제 우리는 각 심볼의 빈도를 고려하면서 머징을 해야한다. 머징을 한 번 할때마다, 참여하는 두 트리의 리프 노드까지 깊이는 각 리프 노드당 1씩 증가한다.
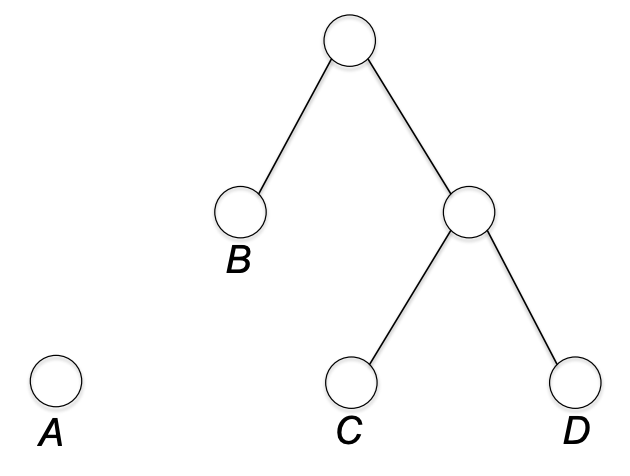
위의 머징 과정(B 트리와 C,D가 있는 트리가 머징되는)을 예로 보자면 C, D의 리프 노드까지 깊이는 1->2 로 증가하고, B는 0->1 로 증가한다. 즉, 심볼을 표현하는 비트 수가 1씩 증가했다. 그러므로 우리는 머징을 하면 비트 수가 증가하고, 우리가 최소화하고자 하는 objective function 인 (평균 리프 depth)도 머징을 함에 따라 증가함을 알 수 있다. 그리고 그리디 알고리즘이라는 말에서 알 수 있듯이 허프만 그리디 알고리즘은 매 이터레이션마다 (평균 리프 depth)을 최소로 증가시키는 방향으로 트리들을 머징해나간다.
Huffman's Greeday Criterion
Merge the pair of trees that causes the minimum-possible increase in the average leaf depth.
그럼 각 머지당 average leaf depth는 얼마씩 증가하는가? 각 트리의 리프 노드 심볼들은 깊이가 1씩 증가한다. 그러므로 각 심볼 는 1* 만큼씩 증가에 기여한다. 따라서 과 를 머징한다고 할때 한 번의 머지에 증가하는 average leaf depth는 다음과 같다.
우리는 이제 이 증가량을 최소로 하는 두 트리를 찾아서 머징시키면 된다. 코드로 보자.
3. Pseudocode
Huffman
// 초기화: 각 라벨 노드를 하나의 트리로 세팅.
for each do
.... := tree containing one node, labeled ""
.... // invariant:
//
// main loop
while contains at least two trees do
.... // smallest frequency sum
.... // 2nd-smallest frequency sum
.... remove and from
.... := merge of and
....
.... add to
return the unique tree in
4. Exmaple
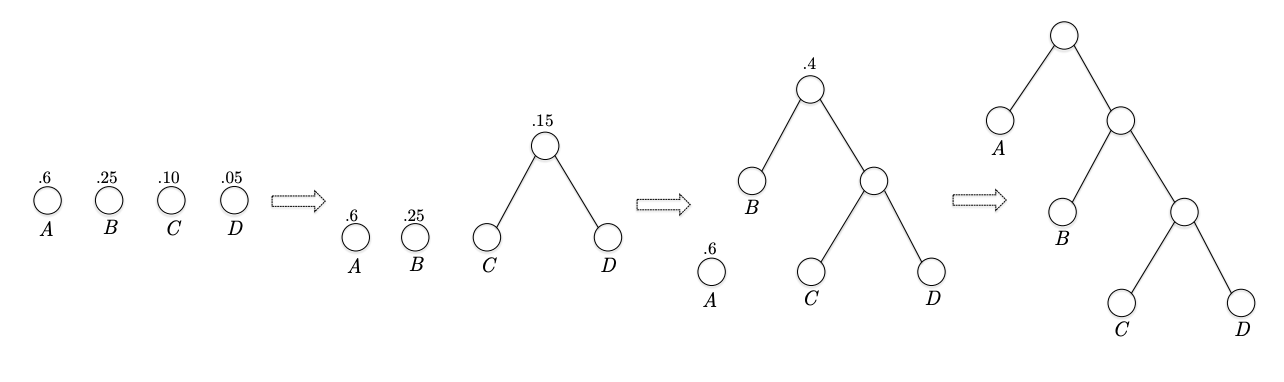
a, b, c, d 가 있고 빈도가 순서대로 .6, .25, .1, .05 라고 하자. 따라서 먼저 c, d를 머징한다. 그럼 a, b, (c,d) 가 있는 트리가 순서대로 .6, .25, .15 의 sum of symbol frequency 를 갖는다. 그 다음은 b, (c,d) 트리를 머징. 그럼 a, (b,c,d) 가 있는 트리가 순서대로 .6, .4 의 sum of symbol frequency 를 갖는다. 남은 둘을 합친다. 그럼 아까 살펴본 variable-length prefix-free code 가 완성된다.