[백준] 1456번 - 거의 소수

---

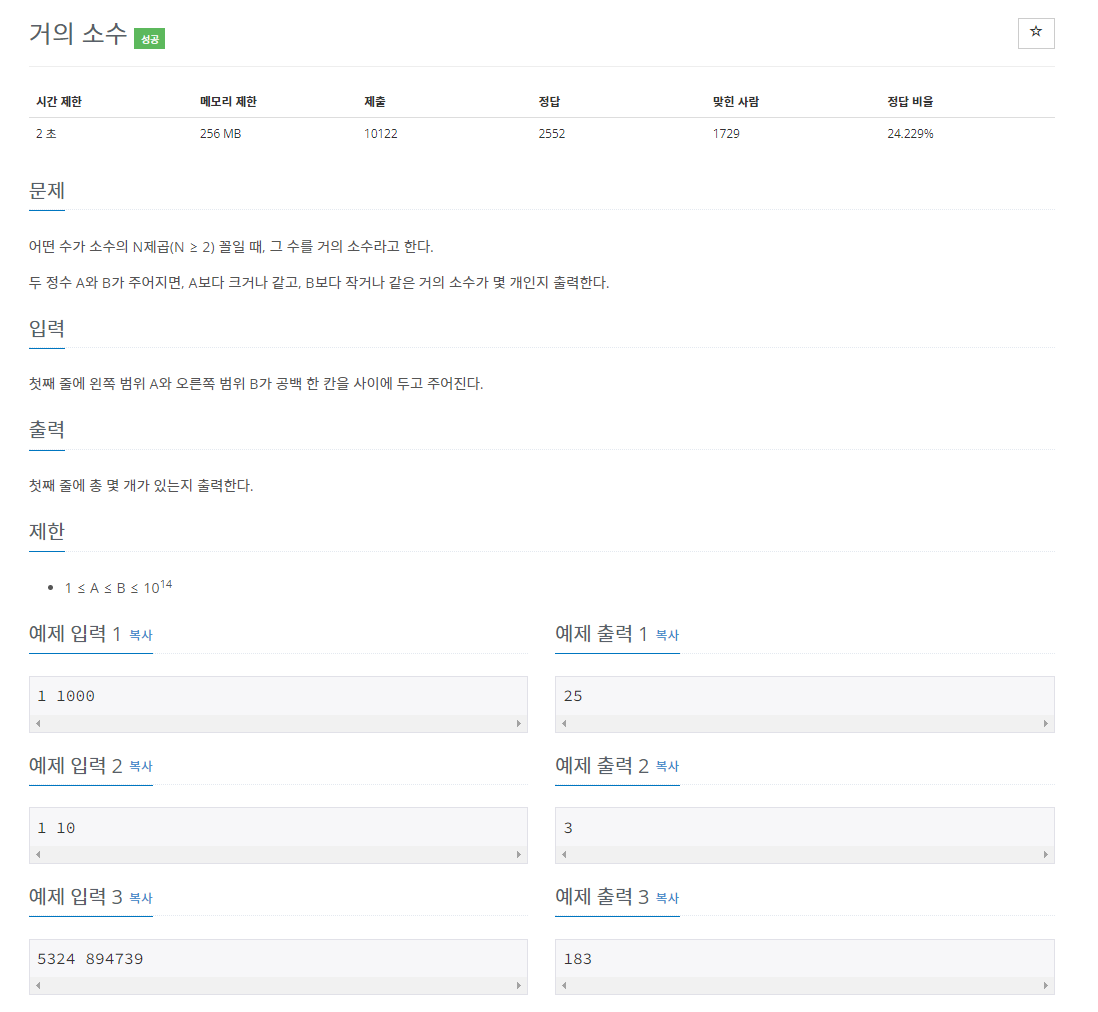
문제 분석

거의 소수를 구하기 위해서는 2부터 주어진 B의 값의 제곱근까지의 수 중 소수인 것들만 찾고, 해당 소수들을 주어진 A와 B사이의 범위에 맞추어 가며 제곱해 나가는 식으로 구하면된다.
여기서 B의 제곱근 까지의 소수를 구하는 이유는 거의소수란 어떤 소수의 N제곱(N>=2)을 의미하며, N의 최소값이 2이기 때문이다.
따라서 B의 제곱근 까지로 범위를 한정해서 생각할 수 있다.
(예를 들어 B의 값이 100으로 주어진다면 10보다 큰 수에 대해서는 고려할 필요가 없기 때문)
따라서 위의 과정에 따라 코드를 구현해 보면 다음과 같다.

---

소스 코드

# 거의 소수

import math
A, B = map(int, input().split())
arr = [0] * (int(math.sqrt(B)) + 1)
prime = []
totalCount = 0

for i in range(2, int(math.sqrt(B)) + 1):
    arr[i] = i

for i in range(2, int(math.sqrt(B)) + 1):
    if arr[i] == 0:
        continue
    else:
        prime.append(arr[i])
        for j in range(i+i, int(math.sqrt(B)) + 1, i):
            arr[j] = 0

for value in prime:
    start = value * value
    while start <= B:
        if start >= A:
            totalCount += 1
        start *= value

print(totalCount)

위에서는 에라토스테네스의 체를 이용하는 방식으로 구현하였다.
또한 prime배열에 있는 값들이 해당 A ~ B의 범위에 해당하는지 비교하는 과정을 통해 카운트값을 증가시켰다.
(여기서 start값이 A보다 작을 수 있지만 계속해서 범위를 비교하는 과정을 통해 start값을 증가시켜 나가는 것이 필요하다.
즉 start값이 처음에는 A보다 작을 지라도 계속해서 곱해가다보면 A이상인 case가 나온다.)