[백준] 1253번 - 좋은 수 구하기

---

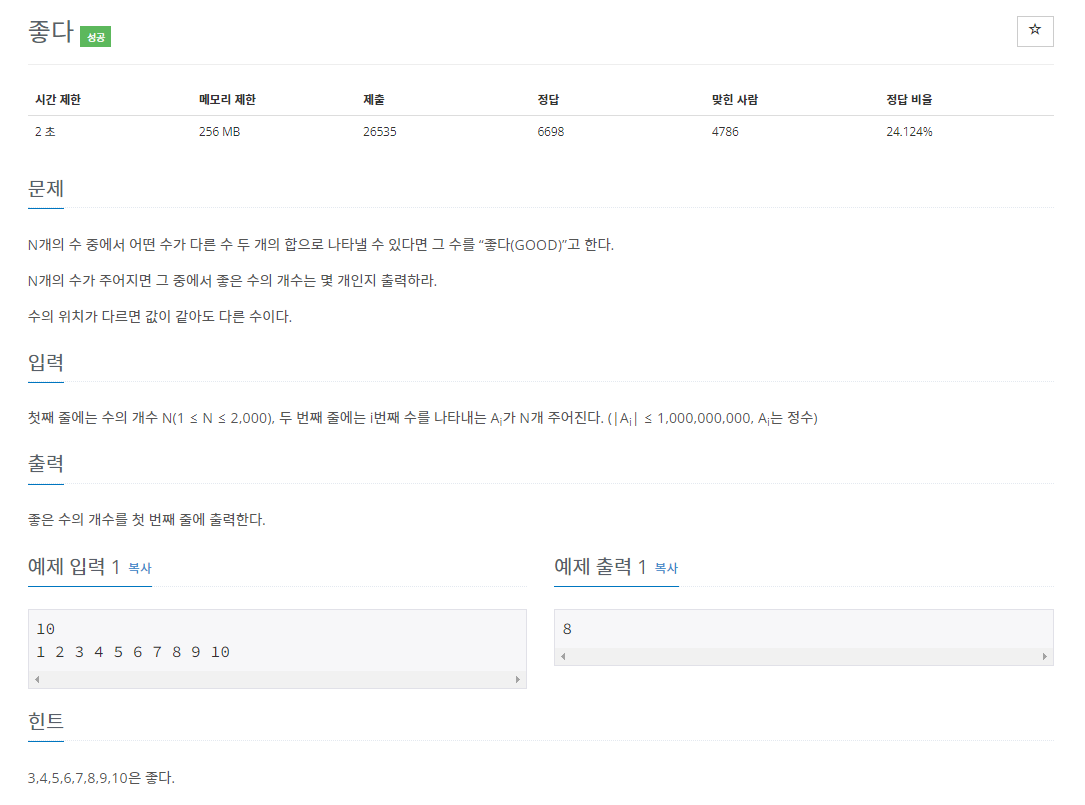
문제 분석

시간 복잡도를 생각해보면, N의 개수가 최대 2000이라 가정해도 좋은 수 하나를 찾는 알고리즘의 시간 복잡도는 N^2보다 작아야 한다.
만약 좋은 수 하나를 찾는데 시간 복잡도가 N^2인 알고리즘을 사용하면 최종 시간 복잡도는 N^3이 되어 제한 시간안에 문제를 풀 수 없게 된다.
따라서 좋은 수 하나를 찾는 알고리즘의 시간 복잡도는 최소 O(nlogn)이어야 하므로, 정렬, 투 포인터 알고리즘을 사용하여 해결하도록 한다.
이때 정렬된 데이터에서 자기 자신을 좋은 수 만들기에 포함하면 안된다는 것에 주의한다.

예시 케이스
-3,0,3 의 경우 => 1
0 0 0 의 경우 => 3

추가로 예시로 -3,-2,-1,0,0,0 인 경우와 0,0,0,1,2,3인 경우에 대해서 어떻게 진행되는지 생각해보면 문제를 푸는데 도움이 될 수 있다.

---

소스 코드

# 좋은 수 구하기

N = int(input())
numList = list(map(int, input().split()))
numList.sort()
count = 0

for i in range(N):
    start = 0
    end = N - 1
    while start < end:
        if numList[start] + numList[end] == numList[i]:
            if start != i and end != i:
                count += 1
                break
            elif start == i:
                start += 1
            else:
                end -= 1
        elif numList[start] + numList[end] < numList[i]:
            start += 1
        else:
            end -= 1

print(count)

---