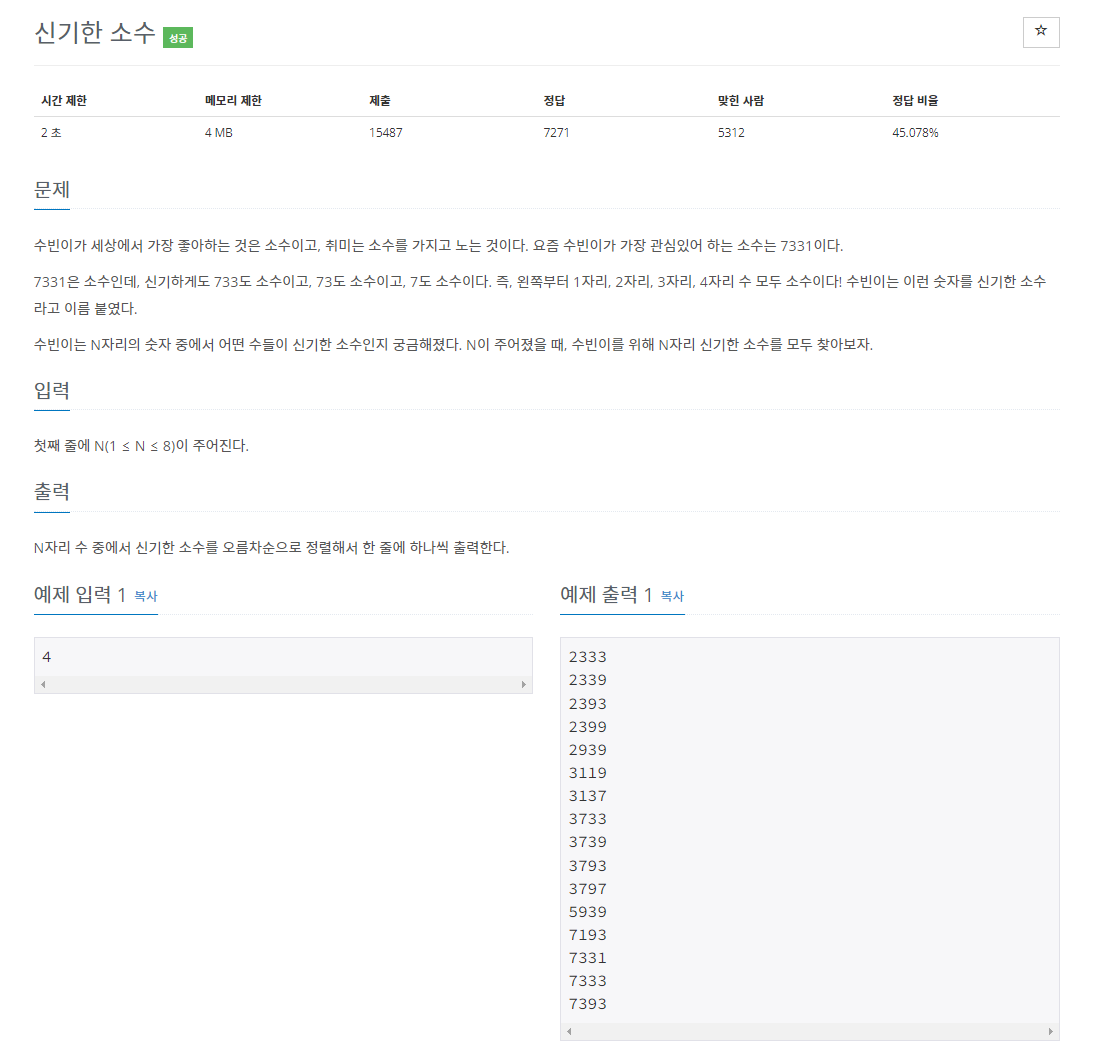
문제 분석
문제를 읽어봤을때, 자릿수에 따라서 해당 숫자가 소수임을 확인해 보야하 하므로 N의 값이 1일때, 2일때, 3일때 어떠한 수가 가능한지를 확인해 보는 과정이 필요하다.
'먼저 N의 값이 1일때, 즉 자릿수가 1자리 인 경우에는 기본적으로 1~9까지의 수 중 소수를 찾아야 한다는 것을 알 수 있으므로, '2,3,5,7'이 가능하다.
이후 N의 값이 2인 경우에는 앞서 구한 '2,3,5,7'에다가 뒤에 홀수의 값인 '1,3,5,7,9'가 올 수 있는 후보라는 것을 알 수 있다.
(홀수가 아닌 짝수, '2,4,6,8'이 오게되면 짝수이므로 소수가 될 수 없으므로 후보에서 제외함.)
따라서 계속해서 이어지는 값은 '1,3,5,7,9'가 될 것이므로 이러한 각각의 케이스에 대해서 소수임을 판별하는 과정이 필요하며, 이때 해당 숫자의 자릿수와 N의 값을 비교해서 동일하게 되는 경우 과정을 종결시키는 매커니즘으로 코드를 짜야함을 알 수 있다.
소스 코드
# 신기한 소수
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
N = int(input())
base = [2, 3, 5, 7]
# 기본적으로 2,3,5,7로 시작되어야 하며 그 뒤에 홀수값인 1,3,5,7,9가 올 수 있다.
# 따라서 1,3,5,7,9를 각각 붙여가면서 소수가 되는지 확인하는 과정을 진행하는 것이 필요하다.
def isPrime(num): # num값이 소수인지 아닌지를 판별하는 함수
for i in range(2, int(num**0.5) + 1):
if num % i == 0:
return False
return True
def recursion(num):
global N
if len(str(num)) == N:
print(num)
else:
for i in [1, 3, 5, 7, 9]:
number = 10*num + i
if isPrime(number):
recursion(number)
for value in base:
recursion(value)추가적으로 소수임을 판별하기 위한 방법들
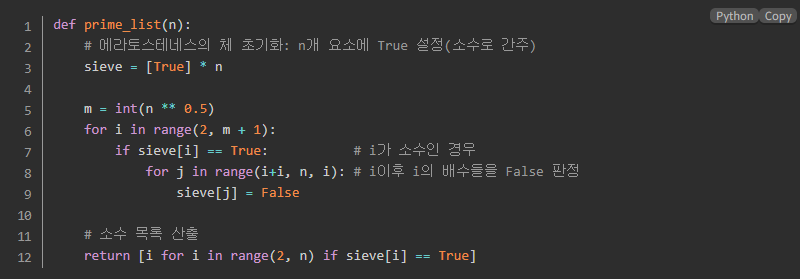
1. '에라토스테네스의 체'를 이용하는 방법
위의 코드는 n미만의 수들 중 소수임을 구하는 코드이다.
2. 제곱근을 이용하여 비교하는 방법