[백준 JAVA]1720 타일코드

import java.util.Scanner;

public class Main {
	private static long dp[]; 
	private static long sym[];

	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		
		int n = scanner.nextInt();
		//1<= N <= 30 이라서 최대갯수대입
		dp = new long[31];
		sym = new long[31];
		
		
		System.out.println(tile_code(n));
	}
	private static long tile_code(int n) {
		return (tile(n)-symmetry(n))/2 + symmetry(n);
	}
	//모든 타일의경우
	private static long tile(int n) {
		if(dp[n] != 0)
			return dp[n];
		if(n == 1)
			return dp[1] = 1;
		if(n == 2)
			return dp[2] = 3;
		
		//dp[n] = ~~~~ - symmetry[n] 이 점화식은
		//전체타일경우의수 - 중복되는타일경우의수 이다.
		dp[n] = tile(n-1) + 2*tile(n-2);
		
		
		return dp[n];
	}
	//좌우대칭인경우
	private static long symmetry(int n) {
		if(sym[n] != 0)
			return sym[n];
		if(n == 1) 
			return sym[1] = 1;
		if(n == 2)
			return sym[2] = 3;
		if(n == 3)
			return sym[3] = 1;
		if(n == 4)
			return sym[4] = 5; 
		
		return sym[n] = symmetry(n-2) + 2*symmetry(n-4);
	}

}

이블로그덕분에 문제해결에 도움이 많이됬다.
https://beginthread.tistory.com/145

모든 타일의 경우의수를 세는것은 dp[n] = dp[n-1 + 2*dp[n-2]; 여기까지는 그려가며 풀렸다. 하지만 이 다음에 중복되는타일제거시 되게 애먹었는데, 위블로그를 보고나서 대칭 이라는 포인트에 중점을 두고, 위 점화식마저 다르게 해석할수있었다.
처음에 점화식세울떄는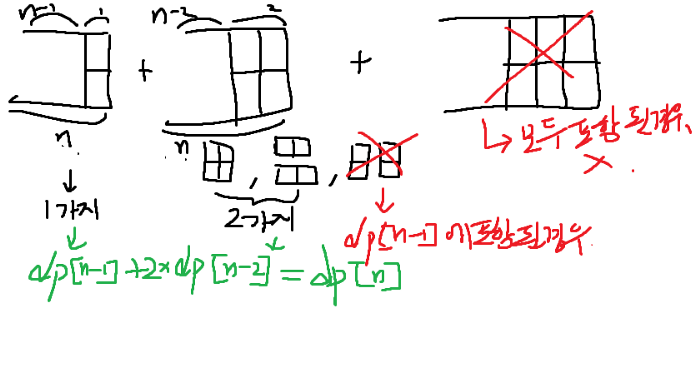
이를 통했지만, 블로그에서

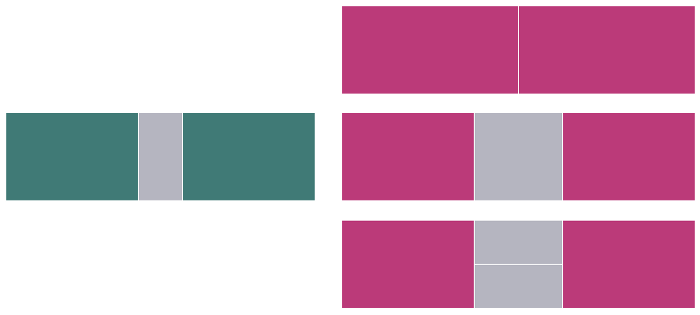
3. s[i]를 가로가 i일때의 경우의 수라고 하면, 좌우가 같은 타일은 대략 s[i/2]라고 생각할 수 있을 것이다. 더 정확하게는 이를 i가 홀수인 경우와 짝수인 경우로 나누어 생각해야 한다.
   홀수인 경우는 가운데에 1x2타일을 두고 좌우가 같은 타일들의 경우가 Y에 해당하므로 s[i/2]이다.
   짝수인 경우는 가운데에 2x(1 or 2)타일을 두고 좌우가 같은 경우 2s[i/2–1]과 사이에 아무 타일이 없는 경우 s[i/2]를 더한 값이다. s[i/2] + 2s[i/2–1]는 s[i/2+1]로 표현 가능하다.

위와 같은 설명을 듣고 중복값처리에대한 구상을 할수 있었다.
따라서 (모든타일경우의수 — 중복되는경우의수) 에서 반을나누고(애초 절반인 반대편경우의수는 *1 로 처리되므로 왜냐면, 깔리는타일은 1.좌우대칭 2.좌우가같음 이므로.) 그 값에 중복되는경우의수를 더하여 결과값을 찾았다.
존나어렵다.. 동적프로그래밍을떠나서 중복값처리가 어려웠다..

https://www.acmicpc.net/problem/1720