[기계학습] Parametric Density Estimation - Maximum A Posteriori Estimation(MAP)
Machine Learning
.png)
Maximum A Posteriori(MAP)
MLE는 model parameter 가 주어졌을 때 모든 observation에 대한 일종의 확률을 나타내는 likelihood의 maximizer를 찾는 optimization problem으로 볼 수 있었다. 또 다시 동전 던지기를 예시로 들어서 이번에는 MAP에 대해서 알아보고자 한다. MLE에서는 앞면이 나올 확률인 를 추정하고자 했다. 흔히 일반적으로 앞면과 뒷면이 나올 확률은 0.5이지만, 우리가 10번 던져서 앞면이 7번 나오게 된다는 사실을 관찰하게 된다면 MLE를 통해서 최대한 가능성이 있는 그럴듯한 값을 0.7로 추정하게 될 것이다. 이는 MLE를 통해서 를 최대로 하고자 했을 때 얻은 결과가 된다.
이렇게 구한 확률도 꽤 만족스럽다. 하지만 우리가 사실 0.5라는 일반적으로 경험 속에서 얻은 값과 MLE를 통해서 추정한 값 0.7 사이에는 어느정도 차이가 존재하고 있다. 0.7의 확률로 앞면이 나오는 동전을 현실 세계에서 보는 것은 쉽지 않을 것이다. 우리의 경험과 지식에 따르면 동전이란 존재는 일반적으로 평평해서 반반의 확률로 앞면과 뒷면이 나오게 된다. 그래서 MLE를 통해 실험으로부터 추정하여 얻은 결과는 단순히 그 결과일 뿐이고, 여기에 현실 세계의 상황을 반영하여 우리의 지식이나 경험을 추가하여 더욱 그럴듯한 확률을 추정하고자 한다. 이때 실험을 통해서 관찰한 어떠한 사실도 아닌 온전히 사전에 알고 있는 지식 등을 추가하고자 하는 것이다. 그래서 우리는 동전이 평평하다는 일종의 belief를 수학적이고 통계적인 상황에 함께 고려하고자 한다. 이러한 과정이 바로 Maximum A Posteriori(MAP)가 되고, MLE 대신에 belief를 추가하여 더욱 가능성이 높은 결과를 추정하고자 한다.
MLE와 마찬가지로 MAP도 parameter 로부터 data 를 만들어내는 probability model 를 가지게 된다. 그러나 차이점이라고 하면 여기에 추가적으로 priori distribtuion 를 가정해서 prior를 정의하는 hyper-parameter 에 대한 의 확률을 추가할 것이다. 이는 우리의 belief, 즉 사전 지식을 model parameter 에 함께 고려하고자 하는 것이다. 우리의 belief를 바꾸거나 조절하고 싶으면 에 해당하는 값을 바꿔주면 된다.
Prior distribtuion을 정의하거나 결정하고 나면 MAP는 posteriori distribtuion 을 최대로 만들려고 노력하게 된다. 그래서 MAP를 통해서 를 최대로 만드는 parameter 를 다음과 같이 구할 수가 있다.
MAP vs MLE
MAP는 다음과 같은 과정으로 를 최대로하는 를 찾게 된다.
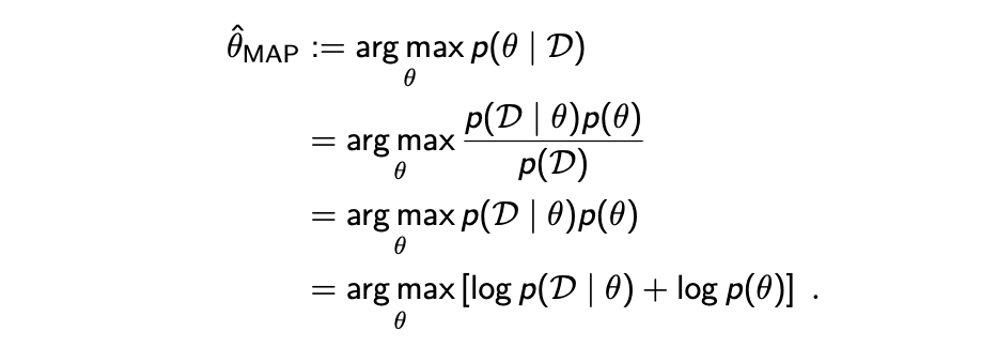 이 과정은 어찌보면 MLE와 같은 과정으로 볼 수 있다. 그러나 MAP에서 posteriori distribution을 바로 사용할 수가 없어서 Bayes' theorem을 이용해서 식을 변형시켜줘야 한다. 식을 변형시켜주게 되면 우리가 이미 알고 있는 likelihood 와 prior 를 사용할 수가 있기 때문이다. Hyper-parameter 는 생략해도 된다. 이러한 수학적인 트릭을 사용해서 이미 알고있는 정보들을 사용해서 계산하여 추정할 수가 있다. 우리는 parameter 에 대해서 distribution 자체를 최대로 만들고자 하는 것이기 때문에 분모에 있는 는 와는 독립적이기 때문에 constant로 간주하여 무시할 것이다. 그러면 결과적으로 우리가 이미 알고 있는 2개의 항 likelihood와 prior만 남게 되어 이제는 MAP를 풀 수가 있게 되었다. 사실 여기서도 수학적으로 편리함을 원하기에 logarithm을 사용해서 식을 summation 형태로 분리시킬 수 있다. 만약 i.i.d.를 만족하는 라고 했을 때 첫번째 를 로 분해할 수 있게 된다. 즉, 각각의 likelihood의 summation으로 표현할 수 있게 된다.
이 과정은 어찌보면 MLE와 같은 과정으로 볼 수 있다. 그러나 MAP에서 posteriori distribution을 바로 사용할 수가 없어서 Bayes' theorem을 이용해서 식을 변형시켜줘야 한다. 식을 변형시켜주게 되면 우리가 이미 알고 있는 likelihood 와 prior 를 사용할 수가 있기 때문이다. Hyper-parameter 는 생략해도 된다. 이러한 수학적인 트릭을 사용해서 이미 알고있는 정보들을 사용해서 계산하여 추정할 수가 있다. 우리는 parameter 에 대해서 distribution 자체를 최대로 만들고자 하는 것이기 때문에 분모에 있는 는 와는 독립적이기 때문에 constant로 간주하여 무시할 것이다. 그러면 결과적으로 우리가 이미 알고 있는 2개의 항 likelihood와 prior만 남게 되어 이제는 MAP를 풀 수가 있게 되었다. 사실 여기서도 수학적으로 편리함을 원하기에 logarithm을 사용해서 식을 summation 형태로 분리시킬 수 있다. 만약 i.i.d.를 만족하는 라고 했을 때 첫번째 를 로 분해할 수 있게 된다. 즉, 각각의 likelihood의 summation으로 표현할 수 있게 된다.
이렇게 식을 정리하고나면 MLE와 MAP를 확실하게 구분할 수 있게 된다. 단 하나의 차이점이라고 한다면 MAP에서는 라는 prior distribtuion을 추가해서 고려해야한다는 것이다. 만약 uniform prior distribtuion이라고 한다면 MAP는 MLE와 같아지게 되고, 따라서 MLE를 MAP의 특수한 경우로 생각할 수 있다. 만약에 가 모든 에 대해서 constant라면 를 MAP라는 maximization problem에서 무시할 수 있게 되고, 결국에 이 두번째 항은 어떠한 영향력도 없어지게 되어 MLE와 같은 상황이 되게 된다.
여기서 또 중요하게 봐야할 부분은 prior이 더해지게 되면 이는 MAP에서 일종의 regularizer의 역할을 하게된다. Machine learning에서 흔히 볼 수 있는 issue로는 overfitting이 있다. Overfitting이란 어떠한 data를 설명하기 위한 model이 있다고 했을 때 likelihood가 1에 가까워지게 되는 상황을 말한다. 우리는 이 값을 조금 잃더라도 overfitting을 막는 것이 더 중요하다. 동전 던지기를 예시로 봤을 때 실제로 앞면의 확률이 0.5라고 했을 때 일반적으로 시도 횟수가 많아질수록 MLE를 통해서 0.5에 수렴하게 될 것이지만, 시도 횟수가 적을 때는 0.5와는 다른 특정 확률을 추정하게 되고 이는 적은 data에 맞춰져서 overfitting이 발생하는 것과 동일한 상황으로 볼 수가 있다. 그래서 이러한 상황을 막고자 belief로 prior를 함께 고려하는 것이고, 이를 overfitting을 막는다는 관점에서 regularizer로 볼 수 있다. 그래서 사실 이 무한정으로 커지게 되면 MAP에서 첫번째 항이 지배적이게 되어 결국 MAP와 MLE가 같아지는 상황에 도달하게 되어 우리의 사전 지식은 더이상 고려되지 않게 된다.
Example of MAP
Example 1: Beta-Binomial
MAP estimation의 예시로 첫번째로는 prior이 Beta distribution, likelihood가 Binomial distribtuion인 상황에 대해서 볼 것이다. 간단하게 Beta distribtuion은 다음과 같다. Beta distribution은 0에서 1까지 정의가 되고 가 parameter인 확률 분포이다.
 여기서 gamma function은 조금 복잡해 보이지만 그 결과는 constant이기 때문에 이후에 고려하지 않게 되어 다음과 같은 결과만 생각해주면 된다.
여기서 gamma function은 조금 복잡해 보이지만 그 결과는 constant이기 때문에 이후에 고려하지 않게 되어 다음과 같은 결과만 생각해주면 된다.
다시 동전 던지는 상황을 예로 들어서 번을 던져서 앞면이 나올 확률 가 미지수인 Binomial distribtuion 에서 우리가 관찰을 했다고 할 것이다. 이때 우리는 사전 지식으로 Beta distribtuion 를 prior로 사용해서 MAP의 해를 추정하고자 할 것이다. 여기서 는 이미 알고 있다. 결국 이 상황은 likelihood는 Binomial, prior는 Beta인 상황이고, MAP의 해를 구하고자 다음의 posteriori distribtuion을 최대로 만드는 를 찾고자 할 것이다.
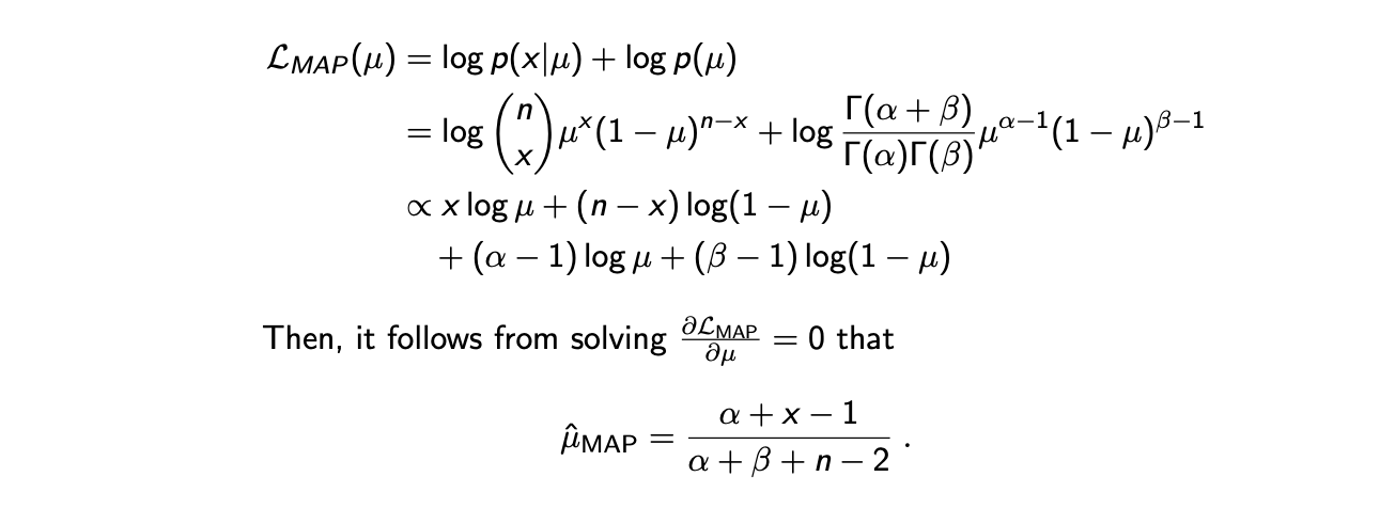 보통 likelihood가 concave인지 보장이 되어야 derivative를 구해서 0으로 두고 해를 찾을 수 있다. 그러나 이미 대부분 자주 사용되는 distribtuion들은 concave가 보장이 되어 있어서 대부분 그냥 진행해주면 된다. 이렇게 MAP estimation을 통해서 우리가 얻고자 하는 MLE보다 더욱 그럴듯한 parameter 를 찾은 것이다.
보통 likelihood가 concave인지 보장이 되어야 derivative를 구해서 0으로 두고 해를 찾을 수 있다. 그러나 이미 대부분 자주 사용되는 distribtuion들은 concave가 보장이 되어 있어서 대부분 그냥 진행해주면 된다. 이렇게 MAP estimation을 통해서 우리가 얻고자 하는 MLE보다 더욱 그럴듯한 parameter 를 찾은 것이다.
그렇다면 이제 추정한 를 확인해보고자 에 3을 대입할 것이다. 그리고 에는 10을 는 7을 대입할 것인데, 같은 상황에서 MLE를 통해서 추정한 는 0.7이었다. 이 값을 그대로 에 대입해보면 0.64가 나오게 되는데, 이는 0.7보다 작아져서 우리가 사전에 알고 있는 평평한 동전의 앞면이 나올 확률 0.5에 더 근사한 것을 볼 수 있다.
앞서 uniform prior의 경우 MAP와 MLE가 같아진다고 했었고, 우리는 이 uniform distribtuion임을 알고 있다. 이 경우 에 1을 대입하면 이 되어 이는 와 같아짐을 확인할 수 있다. 다만 여기서는 1대신에 3으로 설정하여 값을 추정하였고, 그 결과 기존 MLE의 결과보다 0.5에 더 가까운 결과를 추정하게 되었다. 그래서 결국 우리는 prior distribution의 parameter 의 값을 증가시킬수록 0.5라는 확률에 더 가까워짐을 확인할 수 있다. 일반적으로 Beta distribution에서 parameter의 값이 커지는 것은 더 강한 prior를 주는것과 같다.
Example 2: Gaussian
이번에는 prior와 likelihood 모두 Normal distribution인 경우에 대해서 살펴보고자 한다. Dataset 가 을 따르면서 i.i.d.를 만족한다고 가정할 것이다. 여기서 variance는 1로 주어지고 mean만이 미지수 가 되는 것이다. 그리고 여기에 을 따르는 prior distribution 를 사용하고자 한다. 즉, 의 distribtuion이 0 mean Gaussian distribtuion을 만족한다는 것이다. 그러면 이제 MAP estimation을 통해서 다음의 function을 최대로 만드는 parameter를 추정할 것이다.
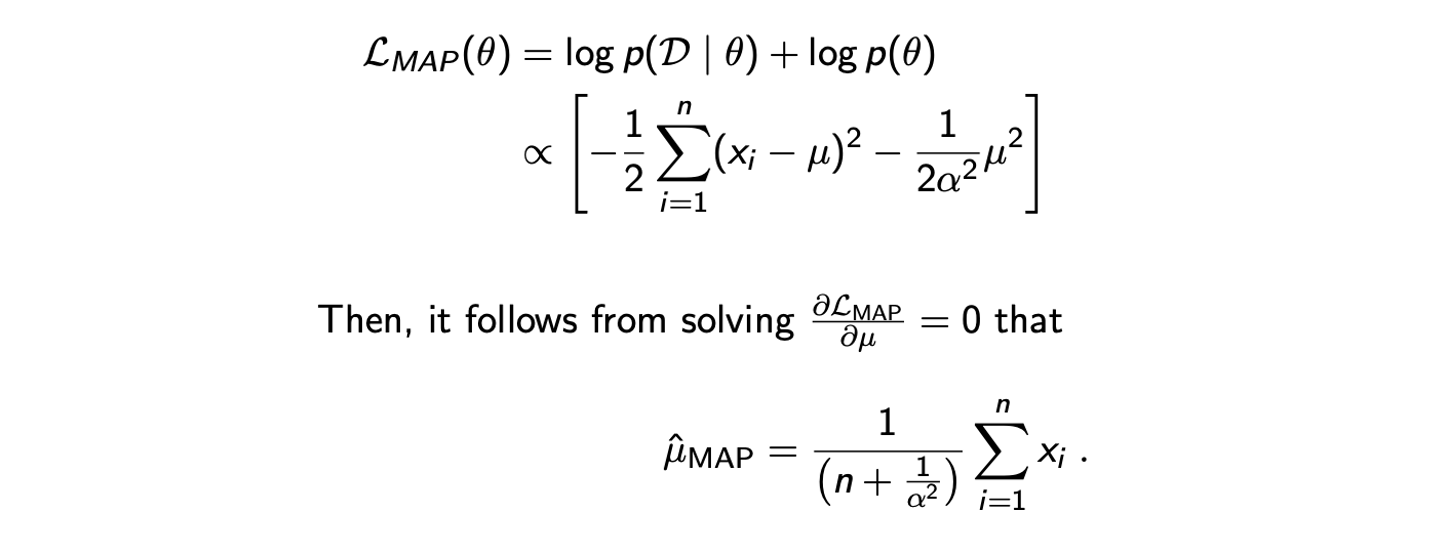 은 확인해보면 알겠지만 concave하기 때문에 stationary point만 찾아주면 그 지점이 최대가 될 것이다. 식만 봐도 미지수 의 최대차수 항의 계수가 음수임을 볼 수 있다. 그래서 derivative를 구하고 0으로 두면 쉽게 를 추정할 수 있다. 추정된 결과를 보면 MLE에서 추정한 empirical mean과 비슷한 형태임을 확인할 수 있다. 단지 prior를 사용했기에 sample의 수인 으로 나누지 않고 으로 나눴음을 확인할 수 있다.
은 확인해보면 알겠지만 concave하기 때문에 stationary point만 찾아주면 그 지점이 최대가 될 것이다. 식만 봐도 미지수 의 최대차수 항의 계수가 음수임을 볼 수 있다. 그래서 derivative를 구하고 0으로 두면 쉽게 를 추정할 수 있다. 추정된 결과를 보면 MLE에서 추정한 empirical mean과 비슷한 형태임을 확인할 수 있다. 단지 prior를 사용했기에 sample의 수인 으로 나누지 않고 으로 나눴음을 확인할 수 있다.
여기서 주목할 부분은 만약 가 매우 작아지게 되면 prior distribtuion이 mean 값인 0에 집중된 형태를 보이게 될 것이다. 이러한 경우에는 MLE와는 크게 관련이 없어지게 되는 반면 가 매우 커져 무한대에 수렴하게 되면 MAP의 결과는 MLE의 결과와 무척 가까어지게 될 것이다. 이를 다시 정리하자면 인 경우에는 prior가 data보다 약해져서, 즉 data가 매우 많을 때는 MAP의 결과와 MLE의 결과가 비슷해지는 반면, 인 경우에는 prior가 data보다 강해져서 MAP의 결과가 0에 수렴하게 될 것이다. Data의 수가 많아지면 결국 prior의 의미가 줄어들게 된다는 것이다.
우리는 결과적으로 적절하고 믿을만한 사전 지식인 belief만 있다면 MLE보다는 MAP를 사용해서 원하는 parameter를 추정하면 된다. 만약, 어떠한 prior도 존재하지 않는 경우라면 보통은 uniform prior를 가지게 될테니 MLE를 사용하기에 좋은 상황이 될 것이다. 그리고 충분히 많은 양의 sample이 존재한다면 굳이 prior를 사용할 필요는 없을 것이다. 보통은 sample의 수가 적은 상황이 대부분일 것이기에 적절한 prior를 선택해서 사용하면 된다.

첫 식에서 10C7이 빠진 것 같습니다