%20Method.png)
Regression
Density estimation을 통해서 관찰된 data로부터 model parameter를 추정할 수 있었고, 이번에는 본격적으로 구체적인 특정 machine learning 기법에 대해서 알아보고자 한다. 가장 먼저 linear regression에 대해서 알아볼 것이며, 이를 이해하기 위해서 먼저 regression에 대해서 알아야 한다. Regression이란 input 와 output 사이의 dependence 를 modeling하고자 초점을 맞춘 학습 기법이다. 예를 들어 사람의 키와 몸무게가 주어졌을 때 이 사람의 기대 수명을 예측하는 상황을 생각해볼 수 있다. 키와 몸무게를 input 라고 하면 기대 수명은 output 가 될 것이다.
일반적으로 이러한 예측하고자 하는 task를 regression task로 다루며 주어진 정보를 기반으로 원하는 결과를 얻고자 학습을 하게 된다. 이때 우리는 항상 완벽하게 예측할 수 없기 때문에 noise factor 을 추가로 필요하게 된다. 이렇게하면 regression task를 다룰 준비가 된 것이다. 그리고 이러한 를 찾은 후에는 새로운 input에 대해서 예측할 수가 있게 되고, 심지어 처음보는 data에 대해서도 결과적으로 예측 결과를 잘 얻을 수 있게 될 것이다. 사실 이러한 부분이 regression이 진정으로 하고자하는 목표이다.
Conditional Mean
이렇게 regression task의 정의에 대해서 알아보았고, 이를 해결하기 위해서는 다음과 같은 error criterior를 생각해봐야 한다. 다시 말해서 regression function에 대해서 좋은 regressor가 되기 위해서는 다음과 같은 error를 최소로 만들어야 하는 것이다.
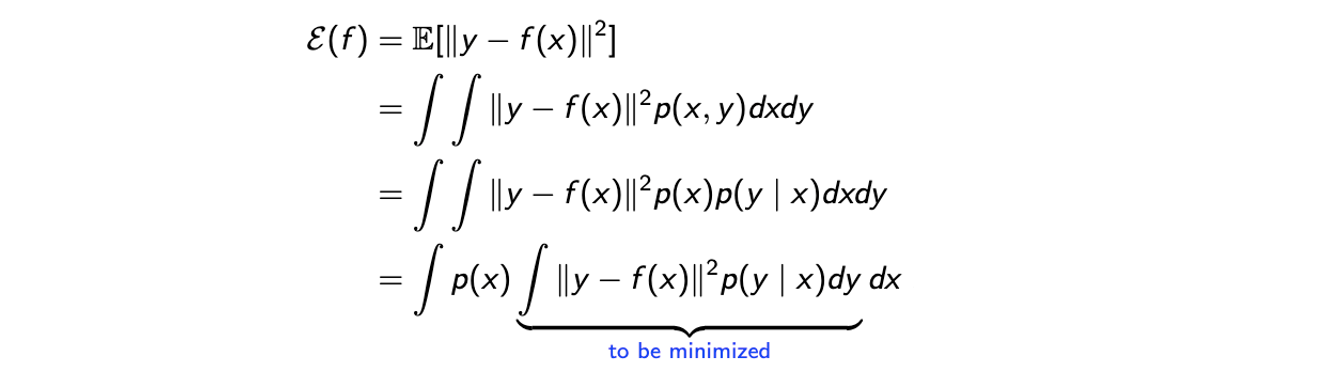 Error function을 어떠한 것을 사용해도 좋지만 일반적으로는 mean squared error(MSE)를 사용하게 된다. MSE는 위와 같이 정의가 되며 이는 regression function의 function이다. 즉, 우리가 찾고자 하는 function 의 성능을 측정할 수 있는 수단이라고 생각하면 된다. 가 주어지게 되면 squared error의 expectation을 구하게 되고, 여기서 는 input이고 는 output이 된다. 결국 우리는 더 나은 예측을 위해서 실제 결과와 예측된 결과 사이의 크기를 줄이고자 하는 것이다.
Error function을 어떠한 것을 사용해도 좋지만 일반적으로는 mean squared error(MSE)를 사용하게 된다. MSE는 위와 같이 정의가 되며 이는 regression function의 function이다. 즉, 우리가 찾고자 하는 function 의 성능을 측정할 수 있는 수단이라고 생각하면 된다. 가 주어지게 되면 squared error의 expectation을 구하게 되고, 여기서 는 input이고 는 output이 된다. 결국 우리는 더 나은 예측을 위해서 실제 결과와 예측된 결과 사이의 크기를 줄이고자 하는 것이다.
첫번째 등호는 MSE의 정의에 따라서 식을 expecation으로 나타낸 것이고 두번째 등호는 이 expecation을 정의에 따라 interal 형태로 바꾼 것이다. 보다시피 여기서 와 의 모든 randomness를 고려해야 해서 의 joint probability를 사용하게 된 것이다. Randomness라는 것은 에서는 input variabel의 distribtuion이고 에서는 에 대한 정보를 가지게 된다. 세번째 등호는 conditional probability의 정의에 따라 식을 다시 나타낸 것이고, 마지막 등호는 marginal probability 가 에 독립적이기 때문에 integral 밖으로 정리를 해준 것이다. 이렇게 식을 정리하게 되면 MSE는 우리가 찾은 가 와 동일할 때 최소를 가지게 되는 것을 쉽게 확인할 수 있다. 이는 에 대해서 derivative를 구하고 0으로 둔 뒤에 값을 찾으면 된다. 여기서 외곽의 integral은 와는 독립적이라 안쪽의 integral에 대해서 최소로 만들어주면 된다. 물론 convexity를 확인했다는 가정으로 최소 지점인 stationary point를 찾는 것이다.
Function Approximation and Curve Fitting
위에서 구한 결과는 regression에서 MSE를 통해서 찾고자 하는 결과이지만, regression task에서 정확하게 를 학습한다는 것은 사실상 불가능하다. 물론 우리가 모든 에 대해서 conditional expectation을 알고있다면 좋겠지만, 가 와 같게 만들기 위해서는 무수히 많은 관찰이 동반되어야 한다. 왜냐하면 여기서 는 real number 혹은 real vector이기 때문에 현실적으로 모든 정보를 안다는 것은 불가능하다. 즉, 모든 가능한 경우에 대해서 학습이 불가능하다는 이야기이기에 현실적으로는 접근하기 위해서는 를 근사할 필요가 있다.
Function approximation을 위한 수많은 후보들이 존재하지만, 가장 유명한 방법으로는 linear function을 사용하는 것이다. 물론 요즘에는 neural network라는 방법을 선택해서 사용하면 된다. 이번에 알아보고자 하는 내용이 linear regression이기에 우리는 에 대해서 linear function을 사용하고자 하는 것이다.
Linear function인 이유는 output 에 대해서 input 의 linear한 형태로 예측이 되기 때문이다. 우리는 사이의 관계에 대한 approximator를 찾는 것이기 때문에 이를 function approximation이라고도 하지만 curve fitting이라고도 한다. 그래서 linear function은 우리의 범위를 linear하게 한정하는 것이고, 수많은 직선들이 data들을 근사시키는 후보가 될 수 있는 것이다. 그리고 우리는 이렇게 수많은 후보군들 중에서 MSE를 최소로 만드는 최적의 해를 찾고자하는 것이다. 물론 이러한 과정을 parameter 에 관한 neural network를 학습시켜서 예측시켜도 된다.
Linear Regression
Linear Models
Model은 function들의 집합으로 생각할 수 있고, linear model은 결국 linear function들의 집합으로 생각할 수 있다. Linear function은 input 와 output 사이의 선형적 관계를 나타낼 수 있다.
위와 같이 vector의 곱으로 나타낼 수 있지만 다음과 같이 matrix 와 vector 의 곱으로 나타낼 수도 있다.
Basis(Feature) Functions
또한 단순한 linear function 대신에 좀 더 복잡한 상황에 유용하게 사용되는 function으로 basis function이 있다. 때때로 input의 차원이 1인 경우가 있는데, 이러한 경우에 linear function 같은 경우 표현하는데 있어 한계가 존재한다. 그래서 이때는 input 를 관심있는 feature로 mapping 해주기 위한 feature function을 사용할 필요가 있다. 수많은 feature function들이 있지만 이 중에서 대표적으로 polinomial function이 존재한다. 그리고 에 대한 feature function 혹은 basis function을 기호로 라고 나타내고자 한다.
예를 들어 polinomial function을 사용하기로 결정했다면 위와 같은 column vector로 나타내서 사용할 수 있다. 그냥 를 사용하기보다 feature function에 대입해서 사용하게 되면 input과 output 사이의 non-linear한 표현을 할 수 있게 된다.
따라서 basis(feature) function을 사용하게 되면 linear model은 input과 output 사이의 non-linear 관계를 modeling 할 수가 있게 되고, basis function은 선택해서 사용하기 나름이다. 어찌됐든 linear function은 basis function으로 확장될 수 있는 것이다.
Linear Regression
우리는 하나가 아닌 여러개의 많은 basis function을 고려할 수 있다. Input 를 차원이라고 했을 때 linear regression은 가 basis function 의 linear combination인 model을 참조하게 된다. 여기서 은 basis function의 수, 즉 feature의 수를 나타낸다. 그래서 이러한 basis function들을 이용해서 다음과 같은 model을 만들 수 있다.
는 feature들의 weighted summation과 같아지게 되며, 편의성을 위해서 모든 를 다음과 같이 vector로 나타낼 수가 있다. 그러면 결과적으로 parameter vector 와 feature vector 의 곱으로 나타내어지게 된다.
결론적으로 여기서 중요한 내용은 feature function으로 linear model의 한계를 보완할 수 있다는 것이다. 자체로는 non-linear하지만 는 미리 주어지기 때문에 여전히 linear regression을 만족하게 된다. 가령 대신에 와 같은 상황이 주어진다면 이 또한 또 다른 linear regression task를 정의하게 되는 셈이다.
Polynomial Regression
이번에는 개념적으로 regression이 하는 것을 알아보고자 한다.
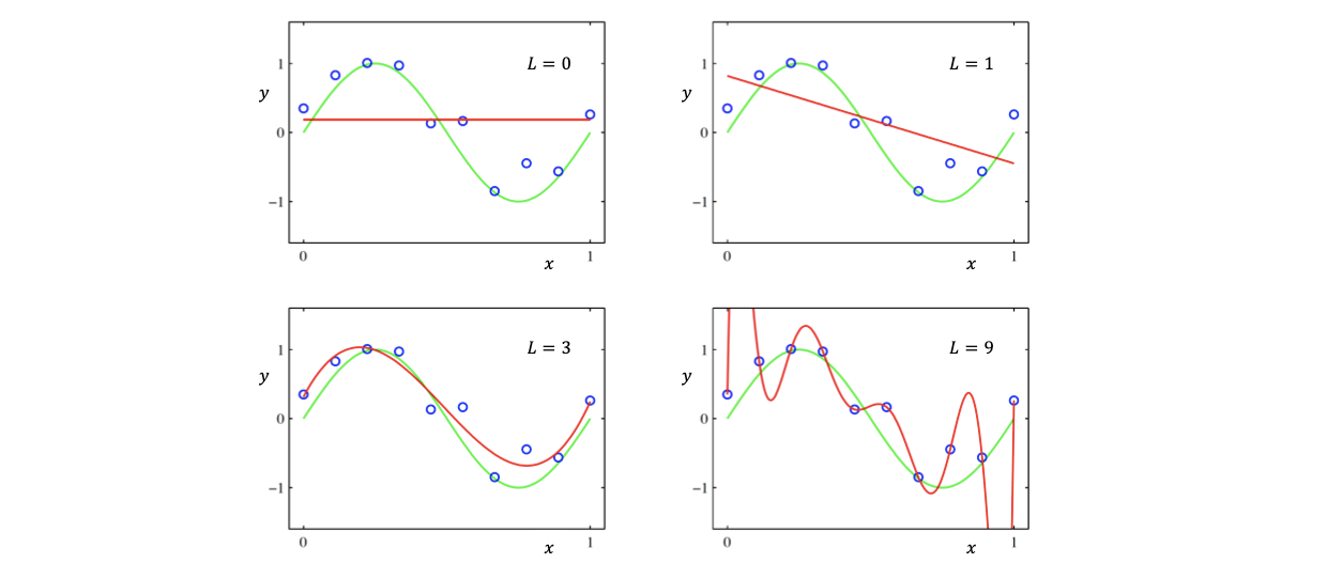 위의 그래프들에서 파란 점은 data point 쌍들이고, 초록 선은 true model을 나타내고 있다. 물론 여기에는 어느정도 noise가 존재해서 이를 감안한 model이고, 만약 feature 수인 이 0인 polynomial regression이라고 한다면 파란 점들을 만족시키기 위해서 빨간 constant line이 만들어질 것이다. 그래서 좌측 위에서 가장 최적의 regressor는 가로로 그은 빨간 constant line이 될 것이다. 만약 여기서 을 증가시켜 1이라고 한다면 는 의 constant가 곱해져 우측 위와 같은 기울기의 regressor가 선택될 것이다. 이렇게 을 계속 증가시켜 어느순간 true model과 근접한 regressor가 형성이 될 것이다. 하지만 이때 만약 을 너무 증가시키게 되면 주어진 파란 점들을 완벽하게 만족하는 error가 0인 regressor가 생길 것이다. 하지만 이러한 경우 true model과는 너무 달라지게 되고 결국 새로운 data에는 적용이 불가능한 overfitting issue를 발생시키게 된다.
위의 그래프들에서 파란 점은 data point 쌍들이고, 초록 선은 true model을 나타내고 있다. 물론 여기에는 어느정도 noise가 존재해서 이를 감안한 model이고, 만약 feature 수인 이 0인 polynomial regression이라고 한다면 파란 점들을 만족시키기 위해서 빨간 constant line이 만들어질 것이다. 그래서 좌측 위에서 가장 최적의 regressor는 가로로 그은 빨간 constant line이 될 것이다. 만약 여기서 을 증가시켜 1이라고 한다면 는 의 constant가 곱해져 우측 위와 같은 기울기의 regressor가 선택될 것이다. 이렇게 을 계속 증가시켜 어느순간 true model과 근접한 regressor가 형성이 될 것이다. 하지만 이때 만약 을 너무 증가시키게 되면 주어진 파란 점들을 완벽하게 만족하는 error가 0인 regressor가 생길 것이다. 하지만 이러한 경우 true model과는 너무 달라지게 되고 결국 새로운 data에는 적용이 불가능한 overfitting issue를 발생시키게 된다.
Fundamental Basis Functions
지금까지 살펴본 polynomial basis 이외에도 여러 다른 흥미로운 basis들이 존재한다.
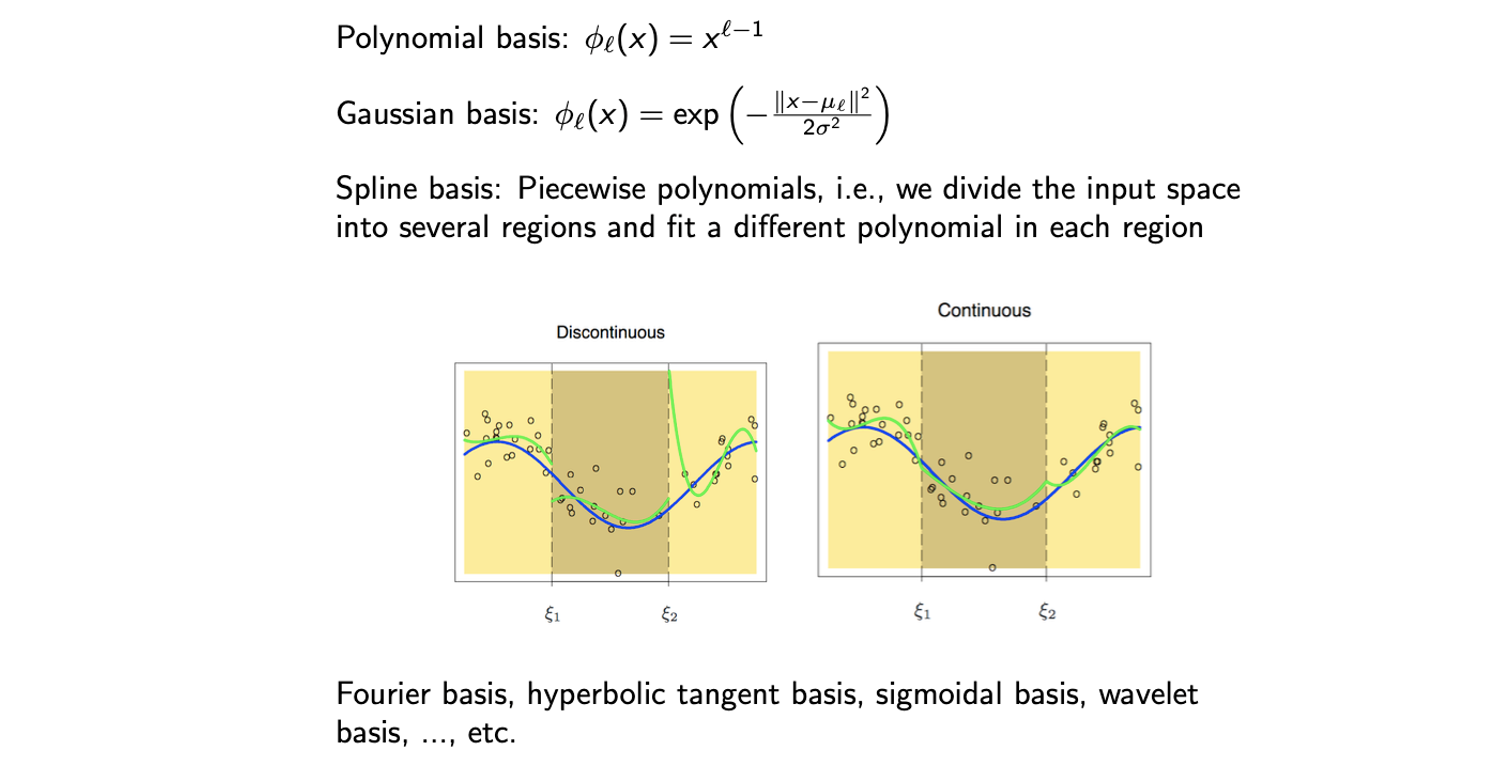 최근에는 모든 basis를 관심있게 사용하지 않으며, Fourier basis나 wavelet basis 등은 여전히 오디오나 영상 데이터에 주로 사용하게 된다.
최근에는 모든 basis를 관심있게 사용하지 않으며, Fourier basis나 wavelet basis 등은 여전히 오디오나 영상 데이터에 주로 사용하게 된다.
Design Matrix
Data 가 개, feature function 가 개가 존재하고 이것들이 집합을 형성하게 되면, 이 집합을 matrix 라 하고 다음과 같이 나타낼 수 있다.
이를 design matrix라 하고, 이 matrix를 통해 regression에서 찾고자 하는 것은 다음과 같은 linear equation을 풀 수 있는 이다.
Least Square(LS) Method
이러한 linear model에서 우리가 풀고자 하는 것은 다음의 loss function을 최소로 만드는 를 찾는 것이다. 다시 말해서 training data 가 주어졌을 때 우리는 다음의 loss function을 최소로 만드는 weight vector 를 결정하고자 한다.
이러한 function을 least square라고 하며, 이는 data point 과 주어진 에 대한 prediction 사이의 squared error를 측정하게 된다. 각 data마다 계산을 해서 summation을 취하게 되지만 이를 vector를 이용하여 한번에 나타낼 수 있다. 앞에 붙은 1/2는 계산의 편의성을 위한 것이고, 전체적으로 위의 식을 통해서 regression task를 해결할 수 있다. 만약 우리의 model이 error가 존재하지 않는다면, 이는 어느 지점에서나 이 0이 되는 것과 같은 이야기이고 결국 위의 식이 최소라는 것은 를 푸는 것과 동일하다는 의미이다.
Least Square Error
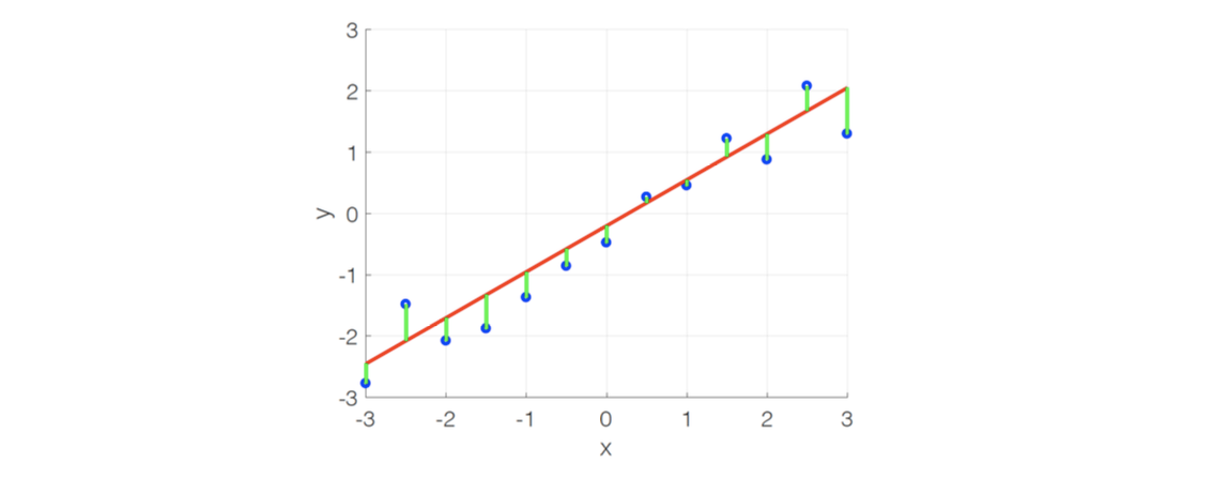
Least square error가 찾으려고 하는 것은 다음과 같이 그래프에 나타내고 있다. 다음과 같이 data point들을 파란 점으로 주어지고 라는 간단한 linear model에 대해서 regression을 수행한다고 해보자. 그러면 최적의 과 는 다음과 같이 초록색의 error를 전부 누적한다고 했을 때 그 결과를 최소로 만들 수 있게 된다.
Least Squre Estimate
그리고 이러한 optimization problem은 실질적으로 closed form solution을 가지고 있게 된다. Closed form solutiond은 다음과 같이 간단한 계산을 통해서 구할 수 있다.
 는 와 같고 이는 에 대해서 convex function이기 때문에 derivative를 구해서 0이 되는 지점이 바로 error를 최소로 만드는 최적의 가 된다. 이렇게 구한 에서 앞에 붙은 것을 우리는 Moore-Penrose pseudo-inverse라고 하고, 이는 inversion의 근사한 결과를 의미하게 된다. 사실 에서 non-zero error라고 했을 때 완전히 등호를 만족시키기 어렵고, 이는 는 non-invertible하다는 의미이기에 inversion을 근사를 시켜야만 했다.
는 와 같고 이는 에 대해서 convex function이기 때문에 derivative를 구해서 0이 되는 지점이 바로 error를 최소로 만드는 최적의 가 된다. 이렇게 구한 에서 앞에 붙은 것을 우리는 Moore-Penrose pseudo-inverse라고 하고, 이는 inversion의 근사한 결과를 의미하게 된다. 사실 에서 non-zero error라고 했을 때 완전히 등호를 만족시키기 어렵고, 이는 는 non-invertible하다는 의미이기에 inversion을 근사를 시켜야만 했다.
Interpretation of LS Method: MLE
지금까지 LS method에 대한 분석을 해보았고, 만약 closed form solution이 존재한다면 기분 좋게 최적의 해를 찾을 수가 있었다. 하지만 현실에서는 다양한 noise들이 존재하고 연구자로서 이러한 LS method에 대한 더욱 근본적인 이유를 찾고자 했다. 그래서 이번에는 MLE를 통해서 LS method를 분석하고 이해해보고자 한다. 이를 진행하기 위해서 먼저 가정을 하고 시작해야 한다. 다음 linear model에서 noise factor 이 평균이 0인 상태라는 가정이 필요하다. 그래서 우리는 이 라는 distribution을 따른다는 가정을 할 것이고, 이를 additive Gaussian noise라고 한다.
이로부터 linear model의 log-likelihood 을 다음과 같이 나타낼 수 있다.
첫번째 등호는 log-likelihood의 정의에 따라 식을 적은 것이다. 여기서 likelihood는 model에서 우리의 observation이 주어졌을 때 output의 확률을 나타낸 것이다. 두번째 등호는 i.i.d.에 의해 log-likelihood를 summation 형태로 분해시킨 것이다. 마지막 등호는 Gaussian model의 정의에 따라 식을 정리한 것이다. MLE가 하고자 하는 것은 위의 log-likelihood를 최대로 만들고 싶은 것이고, 이는 다시 말해서 위의 식에서 마지막 음수 항을 최소로 만들고자 하는 것이고 여기서 괄호 안은 앞서 살펴본 와 동일하다. 그래서 우리는 결국 additive Gaussian noise라는 가정에서 MLE의 해가 LS method의 해와 동일하다는 것을 수식을 통해서 확인할 수 있게 되었다.
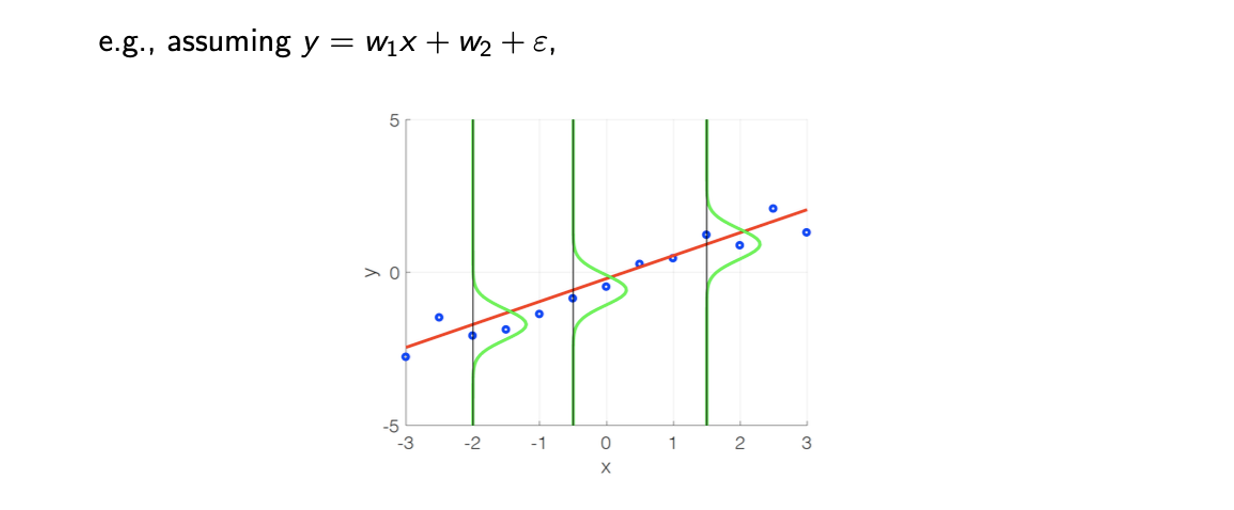 그래프 상에서 확인해보면 파란점을 data point, 빨간선을 라고 했을 때 초록선은 model에 해당하는 부분을 중앙으로 맞춰진 likelihood distribtuion에 대응하게 된다. 여기서 파란점과 빨간선 사이의 squared distance를 최소로 만들고자 하는 것이 LS method가 된다.
그래프 상에서 확인해보면 파란점을 data point, 빨간선을 라고 했을 때 초록선은 model에 해당하는 부분을 중앙으로 맞춰진 likelihood distribtuion에 대응하게 된다. 여기서 파란점과 빨간선 사이의 squared distance를 최소로 만들고자 하는 것이 LS method가 된다.
