
Graphs
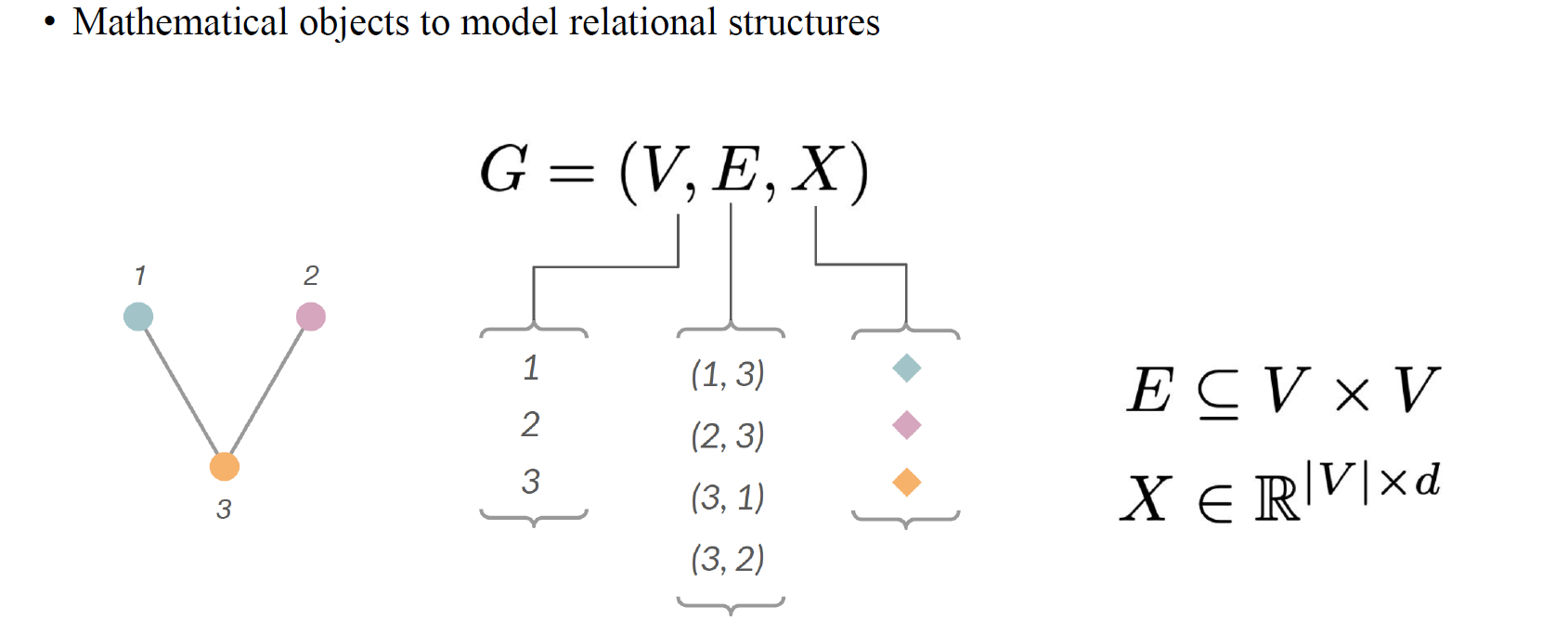 Graph neural network(GNN)의 expressive power를 이야기하기 위해서 결론적으로 WL test를 알아야한다. 우리가 GNN1, GNN2, GNN3가 있다고 했을 때 어느 GNN이 더 좋은지 비교를 하고 싶으며, 이는 expressive power를 통해서 비교가 가능할 것이다. 이를 위해서 GNN의 expressive power를 정량화할 필요가 있고, WL test라는 특정 수단을 통해서 이것이 가능한 것이다. 그전에 graph가 무엇인지부터 알아보도록 하자. Graph 를 우리는 vertex set 와 edge set , 그리고 node feature 로 표현할 수 있다.
Graph neural network(GNN)의 expressive power를 이야기하기 위해서 결론적으로 WL test를 알아야한다. 우리가 GNN1, GNN2, GNN3가 있다고 했을 때 어느 GNN이 더 좋은지 비교를 하고 싶으며, 이는 expressive power를 통해서 비교가 가능할 것이다. 이를 위해서 GNN의 expressive power를 정량화할 필요가 있고, WL test라는 특정 수단을 통해서 이것이 가능한 것이다. 그전에 graph가 무엇인지부터 알아보도록 하자. Graph 를 우리는 vertex set 와 edge set , 그리고 node feature 로 표현할 수 있다.
Graph Representation
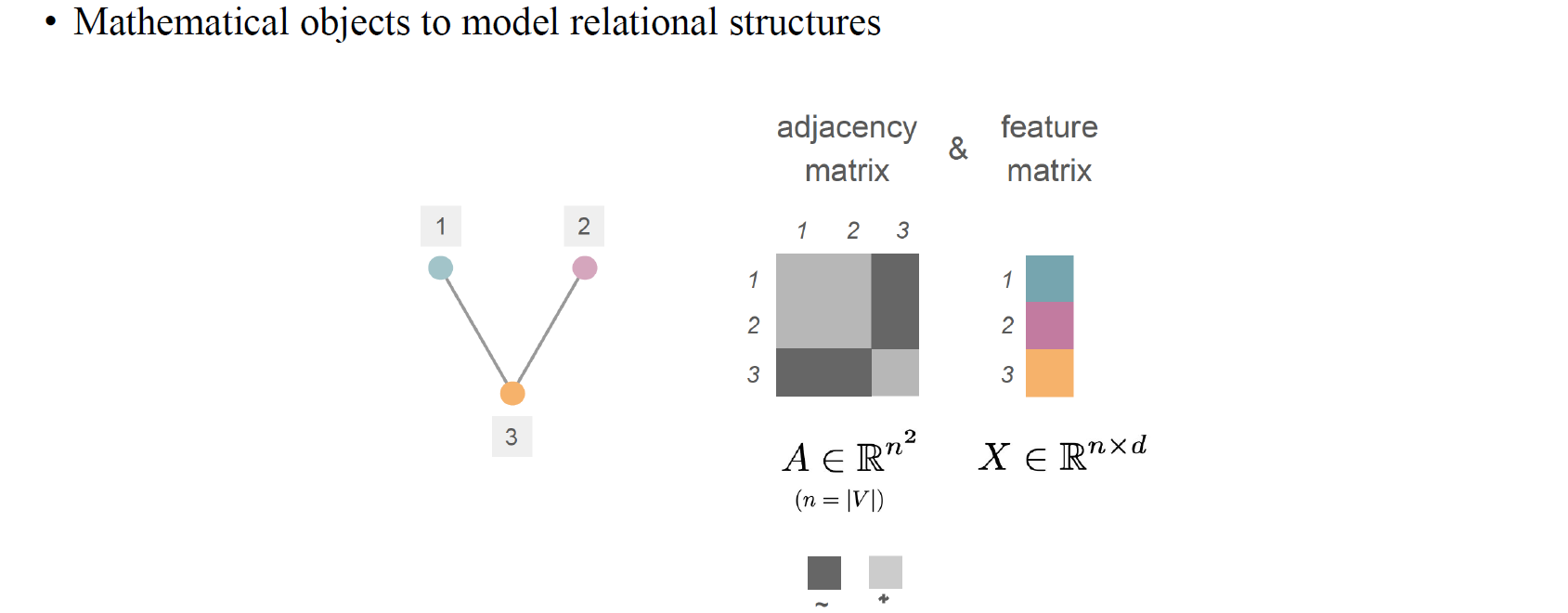 Graph의 representation은 adjacency matrix 와 feature matrix 를 가지고 나타낼 수 있다.
Graph의 representation은 adjacency matrix 와 feature matrix 를 가지고 나타낼 수 있다.
Graph Isomorphism
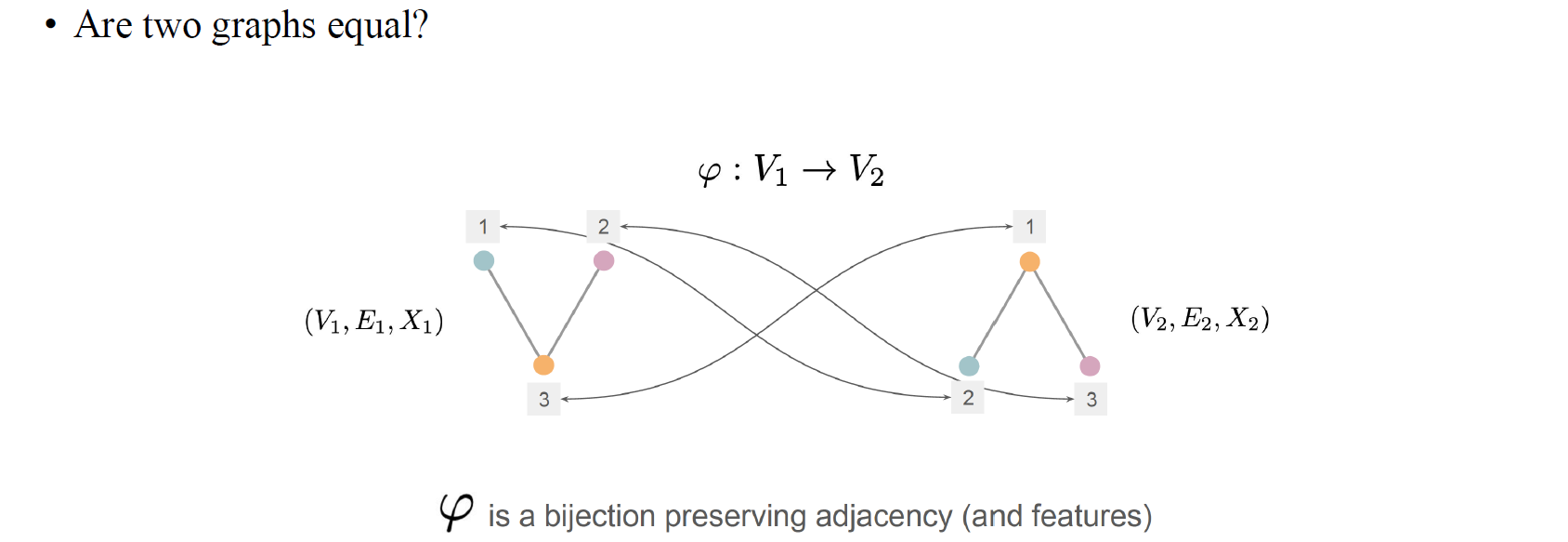 Graph에 대해서 알아보는데 있어서 흥미로운 개념 중 하나가 graph isomorphism이다. 이는 2개의 graph가 형식적으로 동일할 때 사용되는 표현이다. 비록 2개의 graph가 1-2-3과 1-3-2의 형태로 있을지라도 실제로 그 값은 다르지만 graph isomorphism 혹은 adjacency matrix를 보존하는 vertex간 bijection이 있다면 이 둘은 같다고 이야기할 수 있다.
Graph에 대해서 알아보는데 있어서 흥미로운 개념 중 하나가 graph isomorphism이다. 이는 2개의 graph가 형식적으로 동일할 때 사용되는 표현이다. 비록 2개의 graph가 1-2-3과 1-3-2의 형태로 있을지라도 실제로 그 값은 다르지만 graph isomorphism 혹은 adjacency matrix를 보존하는 vertex간 bijection이 있다면 이 둘은 같다고 이야기할 수 있다.
 위와 같이 adjacency preserving의 경우와 feature preserving의 경우를 볼 수 있다. 즉, vertex들의 순서 차이로 인해 다르게 표현되었지만 완전히 같은 구조를 가지고 있으면 graph isomorphism이라고 할 수 있다. 각 vertex가 연결된 구조를 살펴보면 2개의 graph가 정확히 동일하기 때문이다.
위와 같이 adjacency preserving의 경우와 feature preserving의 경우를 볼 수 있다. 즉, vertex들의 순서 차이로 인해 다르게 표현되었지만 완전히 같은 구조를 가지고 있으면 graph isomorphism이라고 할 수 있다. 각 vertex가 연결된 구조를 살펴보면 2개의 graph가 정확히 동일하기 때문이다.
Graph Neural Networks (GNNs)
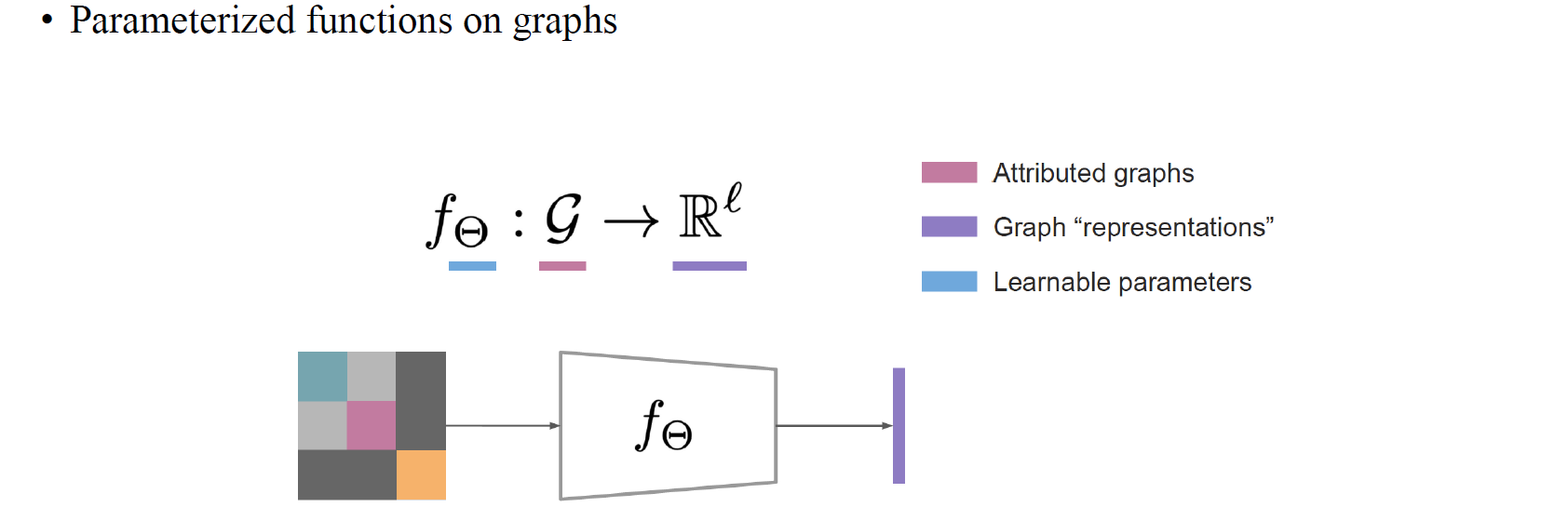 GNN은 graph에 대해서 parameterized된 function이라고 말할 수 있다. 만약 2개의 graph에 대해서 graph isomorphism이 있다면, function 의 output은 항상 동일해야 할 것이다. 하지만 반대로 2개의 graph가 isomorphic하지 않다면 의 output도 isomorphic하지 않을 것이다. GNN은 이러한 개념으로 설명될 수 있다.
GNN은 graph에 대해서 parameterized된 function이라고 말할 수 있다. 만약 2개의 graph에 대해서 graph isomorphism이 있다면, function 의 output은 항상 동일해야 할 것이다. 하지만 반대로 2개의 graph가 isomorphic하지 않다면 의 output도 isomorphic하지 않을 것이다. GNN은 이러한 개념으로 설명될 수 있다.
Message Passing Neural Networks (MPNNs)
 Message passing neural network(MPNN)에서는 각 node마다 node feature가 있을 것이고, 이는 message function과 update function에 의해서 update될 것이다. 여기서 update function은 layer 사이에 non-linearity를 부여하는 역할을 한다.
Message passing neural network(MPNN)에서는 각 node마다 node feature가 있을 것이고, 이는 message function과 update function에 의해서 update될 것이다. 여기서 update function은 layer 사이에 non-linearity를 부여하는 역할을 한다.
Equivariance and Invariance
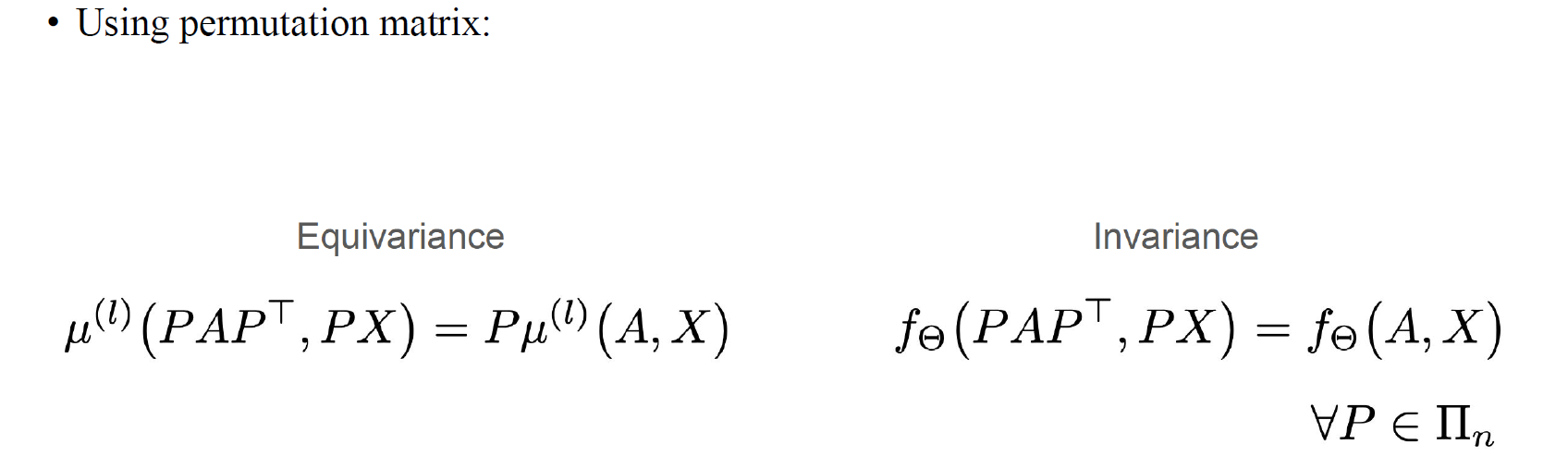 Equivariance와 invariance는 permutation matrix와 관련이 있다. Adjacency matrix 앞뒤로 permutation matrix를 곱할 수 있고, node feature matrix 앞에 permutation matrix를 곱할 수 있다. 이때 output이 permutation matrix에 의해 바뀐다면 equivariance이고, output이 그대로 나오게 된다며 invariance이다.
Equivariance와 invariance는 permutation matrix와 관련이 있다. Adjacency matrix 앞뒤로 permutation matrix를 곱할 수 있고, node feature matrix 앞에 permutation matrix를 곱할 수 있다. 이때 output이 permutation matrix에 의해 바뀐다면 equivariance이고, output이 그대로 나오게 된다며 invariance이다.
MPNNs and Isomorphic Graphs
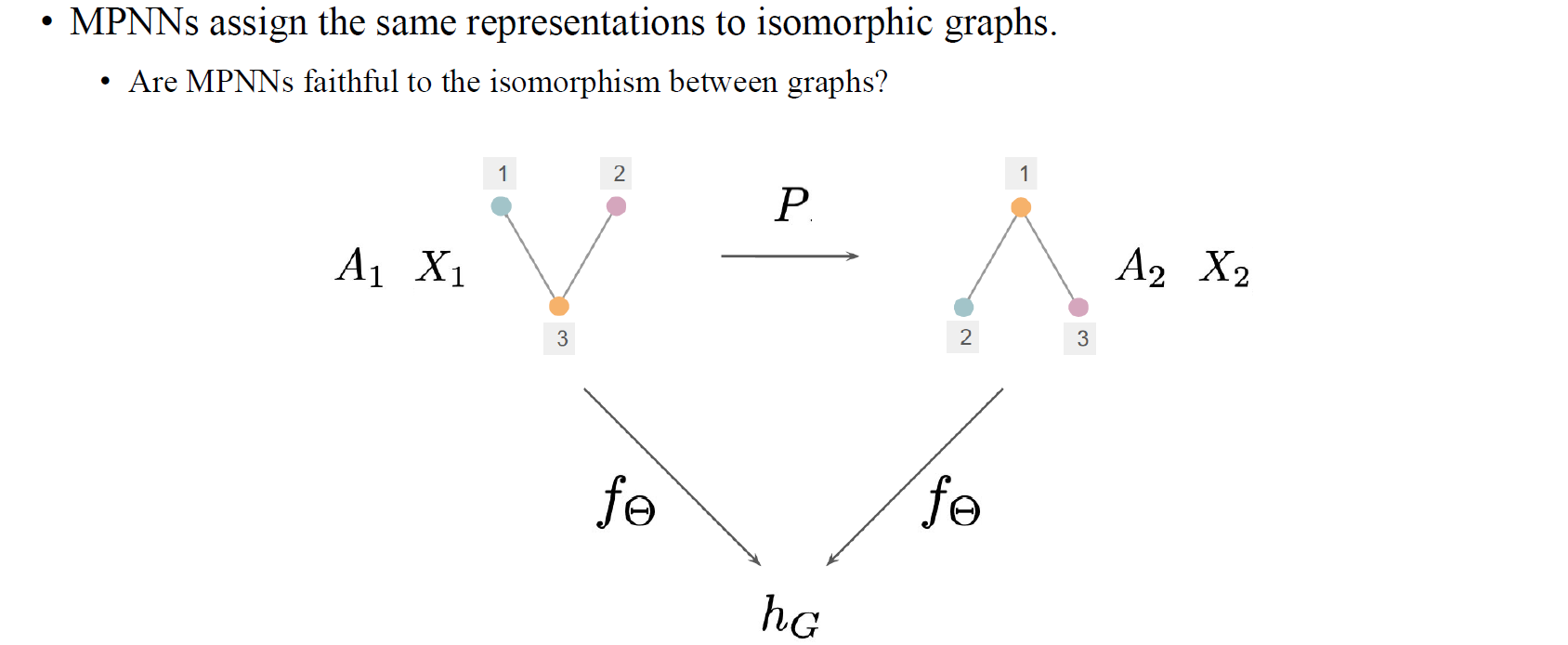 MPNN과 isomorphic graph간 연관성은 흥미로운 부분이 있다. 만약 2개의 graph가 isomorphic하다면, MPNN은 isomorphic graph에 대해서 항상 동일한 representation을 할당하게 된다. 이는 input과 output이 동일하기 때문이다. 하지만, MPNN의 주된 문제점은 혹은 expressive measure를 측정하는데 있어서 만약 2개의 input graph에 대해서 isomorphism이 존재하지 않는다면, output이 여전히 다르다는 것을 보장할 수 없다는 것이다.
MPNN과 isomorphic graph간 연관성은 흥미로운 부분이 있다. 만약 2개의 graph가 isomorphic하다면, MPNN은 isomorphic graph에 대해서 항상 동일한 representation을 할당하게 된다. 이는 input과 output이 동일하기 때문이다. 하지만, MPNN의 주된 문제점은 혹은 expressive measure를 측정하는데 있어서 만약 2개의 input graph에 대해서 isomorphism이 존재하지 않는다면, output이 여전히 다르다는 것을 보장할 수 없다는 것이다.
Representation of Non-Isomorphic Graphs
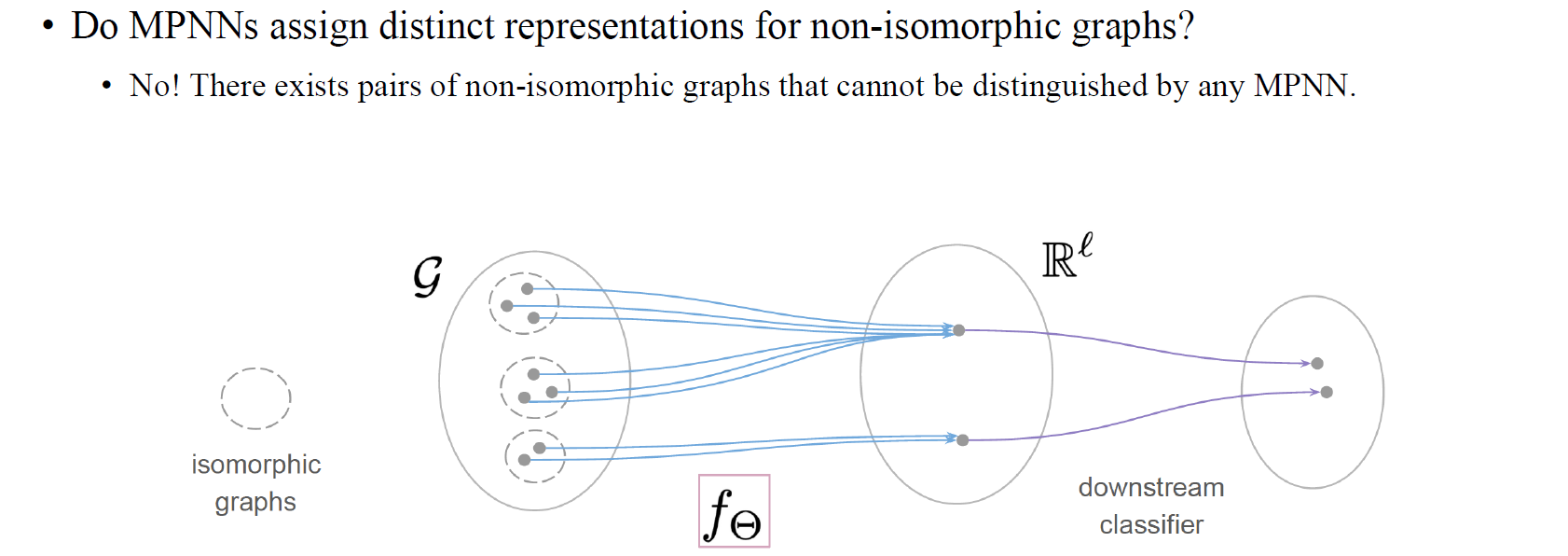 MPNN은 non-isomorphic graph에 대해 고유한 representation을 할당할까? 그 대답은 No이다. 여기에는 어떤 MPNN으로도 구별할 수 없는 non-isomorphic graph의 pair가 존재하기 때문이다. MPNN은 non-isomorphic graph들을 구분할 수 없기에 expressive power를 가지고 있지 않고, 이는 중요한 문제로 남아있다. 위의 그림에서 dash로 연결된 cluster들은 isomorphic graph들의 set이다. 3개의 isomorphic graph 중에서 위의 2개는 서로 다른 graph임에도 MPNN에 의해 동일한 representation으로 mapping된 것을 볼 수 있다.
MPNN은 non-isomorphic graph에 대해 고유한 representation을 할당할까? 그 대답은 No이다. 여기에는 어떤 MPNN으로도 구별할 수 없는 non-isomorphic graph의 pair가 존재하기 때문이다. MPNN은 non-isomorphic graph들을 구분할 수 없기에 expressive power를 가지고 있지 않고, 이는 중요한 문제로 남아있다. 위의 그림에서 dash로 연결된 cluster들은 isomorphic graph들의 set이다. 3개의 isomorphic graph 중에서 위의 2개는 서로 다른 graph임에도 MPNN에 의해 동일한 representation으로 mapping된 것을 볼 수 있다.
An abstract Example
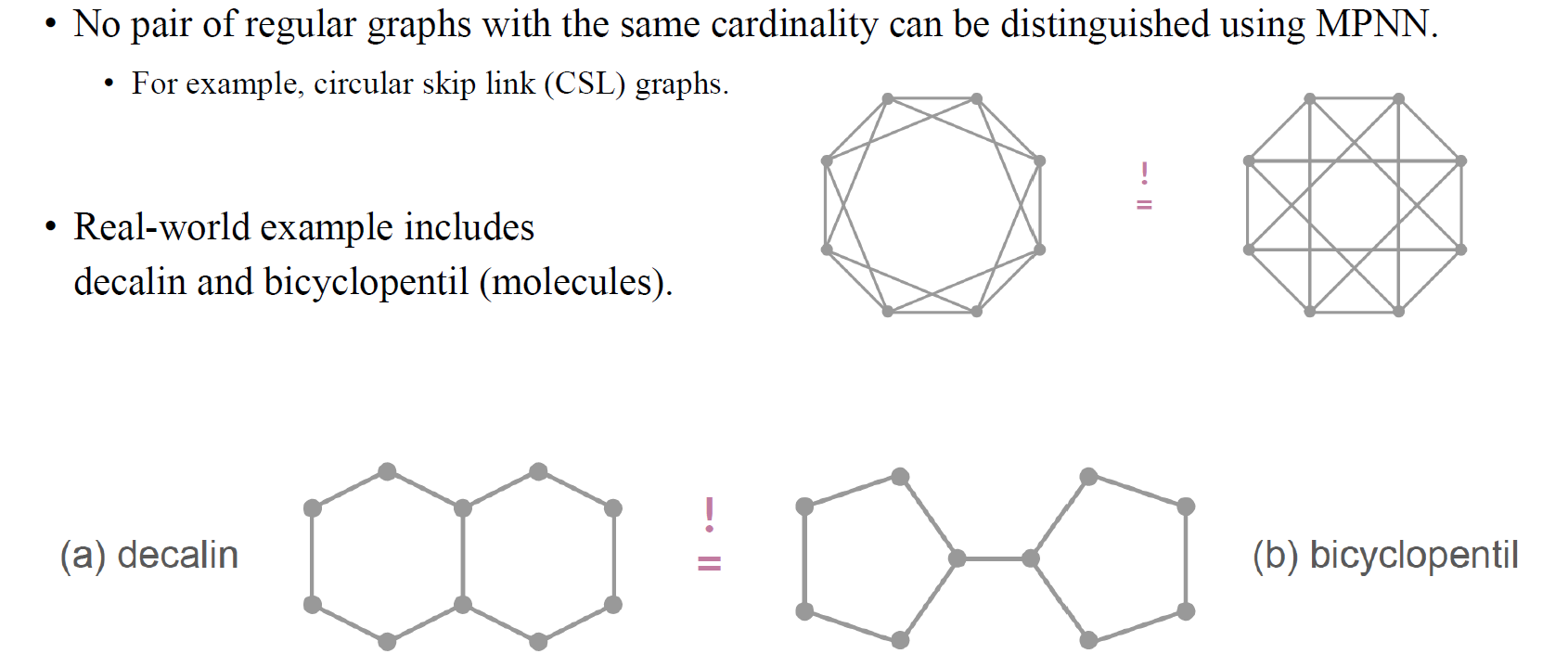 더 유명한 예시 중 하나로 MPNN에 의해 구별될 수 없는 isomorphic graph로 regular graph가 있다. 위의 regular graph 예시에서 좌측의 graph는 옆의 node 하나를 건너 뛰어서 edge를 생성하였지만 우측의 graph는 2개의 node를 건너 뛰어서 edge를 생성하였다. 즉, 좌측의 graph는 cycle이 3이고, 우측의 graph는 cycle이 4이다. 우리는 이러한 graph들을 circular skip link (CSL) graph라고 부르며, GNN이 쉽게 구분하지 못하는 대표적인 graph 중 하나이다. GNN의 첫번째 layer에서 모든 vertex를 구분할 수 없을 것이다. 두번째 layer에서는 4개의 vertex에 대한 message를 모을 것이다. 좌측의 graph와 마찬가지로 우측의 graph도 두번째 layer에서 4개의 vertex에 대한 정보를 얻게 된다. 이렇듯 양쪽 graph 모두로부터 local neighbor structure가 동일해서 GNN이 쉽게 구분하기 어려울 것이다. Message passing이 얼마나 복잡하거나 non-linearity가 어떻든 상관없이 두 graph의 output은 동일하게 나올 수 있다. 또한, MLP를 깊게 쌓더라도 두 graph를 구분하는 것은 쉽지 않을 것이다.
더 유명한 예시 중 하나로 MPNN에 의해 구별될 수 없는 isomorphic graph로 regular graph가 있다. 위의 regular graph 예시에서 좌측의 graph는 옆의 node 하나를 건너 뛰어서 edge를 생성하였지만 우측의 graph는 2개의 node를 건너 뛰어서 edge를 생성하였다. 즉, 좌측의 graph는 cycle이 3이고, 우측의 graph는 cycle이 4이다. 우리는 이러한 graph들을 circular skip link (CSL) graph라고 부르며, GNN이 쉽게 구분하지 못하는 대표적인 graph 중 하나이다. GNN의 첫번째 layer에서 모든 vertex를 구분할 수 없을 것이다. 두번째 layer에서는 4개의 vertex에 대한 message를 모을 것이다. 좌측의 graph와 마찬가지로 우측의 graph도 두번째 layer에서 4개의 vertex에 대한 정보를 얻게 된다. 이렇듯 양쪽 graph 모두로부터 local neighbor structure가 동일해서 GNN이 쉽게 구분하기 어려울 것이다. Message passing이 얼마나 복잡하거나 non-linearity가 어떻든 상관없이 두 graph의 output은 동일하게 나올 수 있다. 또한, MLP를 깊게 쌓더라도 두 graph를 구분하는 것은 쉽지 않을 것이다.
두번째 유명한 예시는 화학에서의 molecule graph로 decalin과 bicyclopentil이 있다. 두 graph 모두 degree가 2인 vertex가 8개 있고 degree가 3인 vertex가 2개 있다. 그리고 degree가 3인 vertex 중 2개는 degree가 2인 vertex들과 연결되어 있고, 나머지 1개는 degree가 3인 vertex와 연결되어 있다. 지역적인 관점에서 이 2가지 graph를 구분하는건 불가능할 것이다.
Universal Approximation
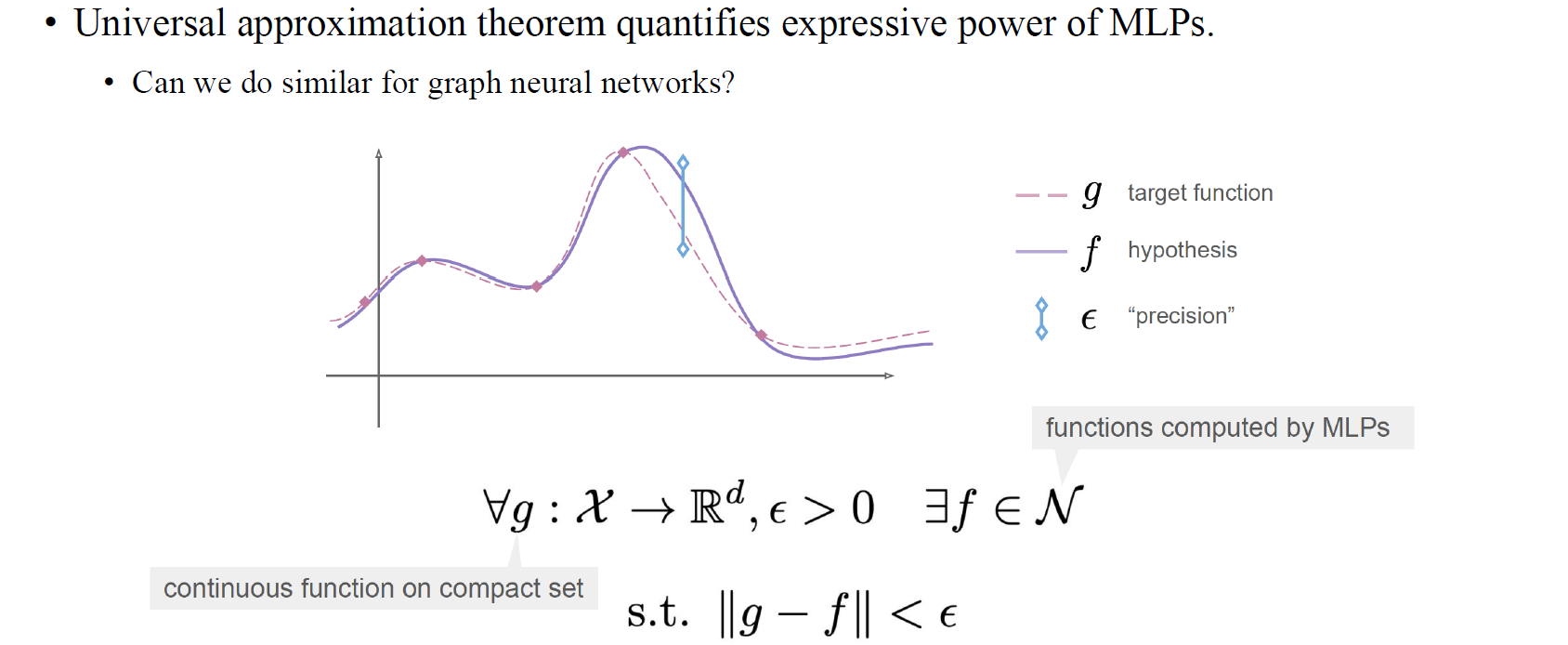 우리는 이를 universal approximation theorem과 관련해서 볼 수 있다. Universal approximation theorem은 MLP와 같은 neural network의 expressive power를 정량화할 수 있다. 만약 function이 존재한다면 만약 충분한 수의 neuron을 사용할 수 있다면, 값에 따라 function 를 근사하는 MLP를 만들 수 있다.
우리는 이를 universal approximation theorem과 관련해서 볼 수 있다. Universal approximation theorem은 MLP와 같은 neural network의 expressive power를 정량화할 수 있다. 만약 function이 존재한다면 만약 충분한 수의 neuron을 사용할 수 있다면, 값에 따라 function 를 근사하는 MLP를 만들 수 있다.
Function Approximation and Graph Discrimination
 그러나 이전의 GNN의 결과는 universal approximation theorem과 같이 function을 근사했을 때 그 결과가 일치하지 않았다. 왜냐하면 2개의 graph가 isomorphic하지 않을 때 GNN을 얼마나 복잡하게 만드는 것과 상관없이 특정 constraint를 넘지 못하기 때문이다. 그리고 이는 참일 필요는 없다. 여기서 주된 문제점은 GNN이 MLP와는 다르다는 것이다. 여기서 우리가 해야하는 것은 expressive power를 측정하는 또 다른 축을 정의하는 것이다.
그러나 이전의 GNN의 결과는 universal approximation theorem과 같이 function을 근사했을 때 그 결과가 일치하지 않았다. 왜냐하면 2개의 graph가 isomorphic하지 않을 때 GNN을 얼마나 복잡하게 만드는 것과 상관없이 특정 constraint를 넘지 못하기 때문이다. 그리고 이는 참일 필요는 없다. 여기서 주된 문제점은 GNN이 MLP와는 다르다는 것이다. 여기서 우리가 해야하는 것은 expressive power를 측정하는 또 다른 축을 정의하는 것이다.
그래서 GNN의 expressive power를 어떻게 정량화하여 측정해야 하는 것일까? Graph를 input으로 가지는 GNN이 있을 때 function의 class는 non-isomorphic graph의 pair를 구별할 수 있는 경우에만 보편적으로 근사될 것이다. 만약 우리의 GNN이 보편적으로 근사시키고자 한다면 GNN이 non-isomorphic graph의 pair를 구별하는 추가적인 constraint를 통합시켜야 할 것이다.
MPNNs and Function Approximation
 Permutation에 invariant한 function들의 class가 존재한다고 해보자. 이는 graph에 대해서 동작하는 operation이기 때문이 이러한 가정이 가능하다. 그러나 이 function들의 class가 neuron을 얼마나 많이 사용하는지와 상관없이 MPNN에 의해 근사되는 function들과 완전히 일치하지는 않는다. 위에서 은 function 의 strict subset이다. 이것이 의미하는 것은 이 보편적으로 근사되지 않는다는 것이다.
Permutation에 invariant한 function들의 class가 존재한다고 해보자. 이는 graph에 대해서 동작하는 operation이기 때문이 이러한 가정이 가능하다. 그러나 이 function들의 class가 neuron을 얼마나 많이 사용하는지와 상관없이 MPNN에 의해 근사되는 function들과 완전히 일치하지는 않는다. 위에서 은 function 의 strict subset이다. 이것이 의미하는 것은 이 보편적으로 근사되지 않는다는 것이다.
Substructure-Counting is Not in
 MPNN은 graph에서 유도되는 subgraph들을 셀 수 없다. Induced subgraph는 vertex 중 일부와 이들과 연결되는 edge들이 선택된 graph이다. 만약 graph 의 ring 개수에 graph 를 대응시키는 function이 있다면, 이 function들이 존재한다는 것을 증명할 수 있을 것이다.
MPNN은 graph에서 유도되는 subgraph들을 셀 수 없다. Induced subgraph는 vertex 중 일부와 이들과 연결되는 edge들이 선택된 graph이다. 만약 graph 의 ring 개수에 graph 를 대응시키는 function이 있다면, 이 function들이 존재한다는 것을 증명할 수 있을 것이다.
Expressive Power of GNNs
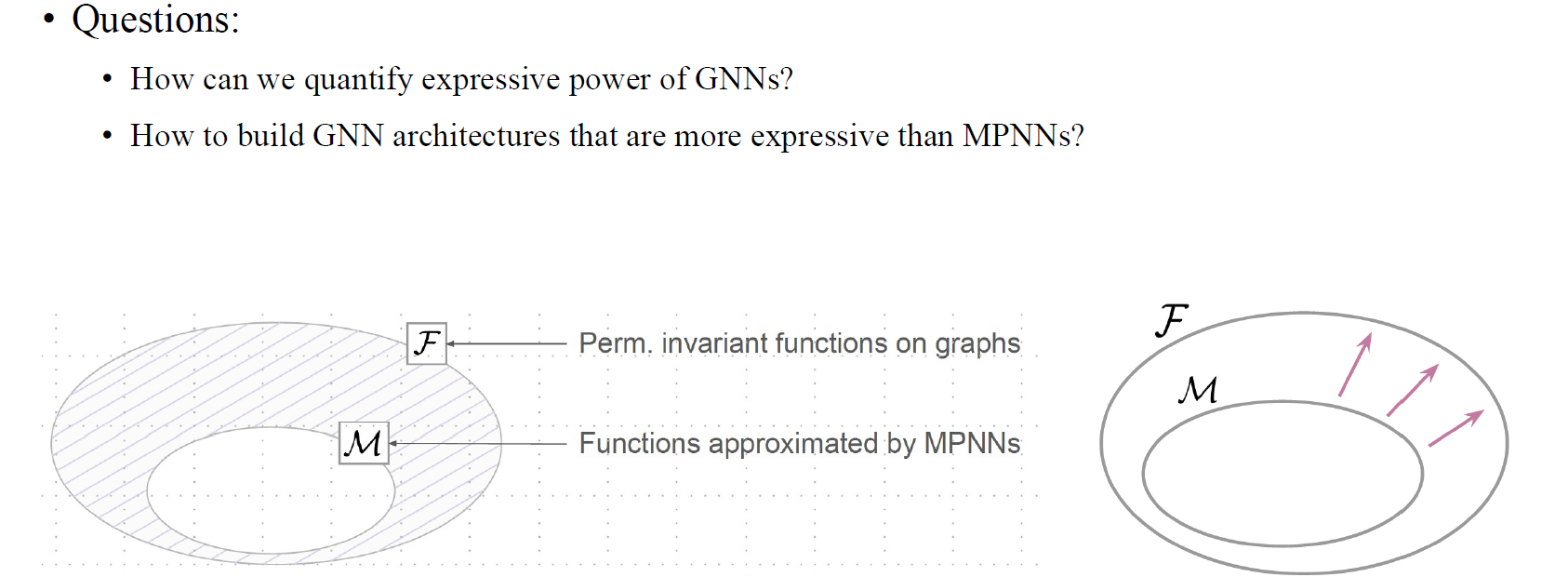 기존의 MPNN은 안에 존재하는 class들을 가지고 있다. 하지만 GNN의 expressive power를 수치화할 수 있다면 expressive power의 위계를 세울 수 있을 것이다. 우리는 새로운 architecture를 설계함으로써 GNN이 표현할 수 있는 function의 class를 증가시킬 수 있다.
기존의 MPNN은 안에 존재하는 class들을 가지고 있다. 하지만 GNN의 expressive power를 수치화할 수 있다면 expressive power의 위계를 세울 수 있을 것이다. 우리는 새로운 architecture를 설계함으로써 GNN이 표현할 수 있는 function의 class를 증가시킬 수 있다.
