[그래프 기계학습] Blueprint for Geometric Deep Learning

Groups and Symmetries

이번에는 geometric deep learning (GDL)과 관련하여 blueprint를 설명하려고 한다. 여기서 blueprint라는 것은 우리가 CNN, GNN 등을 표현하는데 있어서 중요한 formula를 설명하려고 하는 것이다. 우리가 GDL을 설명할 때마다 group과 symmetry라는 개념을 빼놓을 수는 없다. 이는 group theory라고 하는 분야에서 주로 등장하는 개념들이다. Group theory는 다소 어려울 수 있지만 그 아래에 놓여있는 개념들은 다소 간단하게 설명될 수 있다. 이들은 실제로 transformation으로 인하여 자연스럽게 등장한 개념들이다.

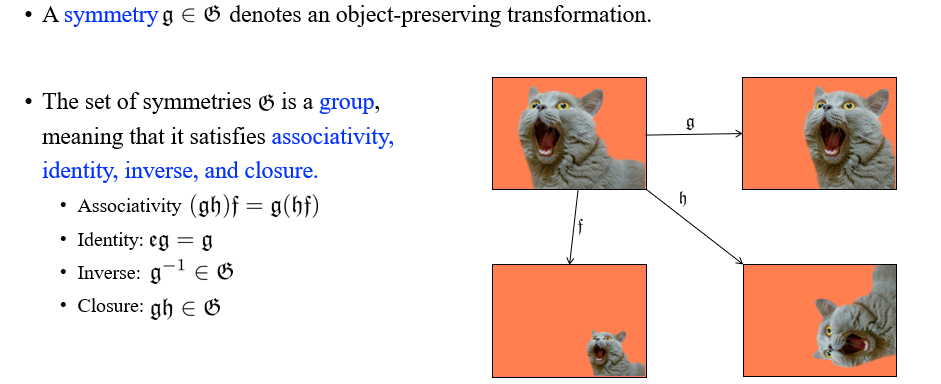
그렇다면 여기서 group과 symmetry가 의미하는 것은 무엇일까? 앞으로 symmetry에 관하여 정말 많이 이야기를 할 것이고, symmetry를 어떤 object를 보존하는 transformation으로서 여길 것이다. 여기서 object를 보존한다는 것은 어떠한 의미가 정해져있다기 보다는 우리가 정하기 나름이다. 이는 언제든지 정하기에 따라 달라질 수 있는 것이다. Image에서 symetry는 translation, rotation, squashing 등에 해당할 수 있다. 즉, transformation의 composition을 symmetry로 생각할 수 있다는 것이다.

만약 symmetry가 존재한다면, object를 보존하는 transformation을 가지는 element가 있다는 것이다. 그렇다면 여기서 object를 보존하는 transformation을 나타내는 set $\mathfrak{G}$는 무엇일까? 우리는 symmetry들의 set인 $\mathfrak{G}$를 group으로 부를 것이다. Group이라는 것은 결국 4가지 성질들(associativity, identity, inverse, closure)을 만족하는 symmetry 혹은 transformation들의 set을 의미하게 된다. 가장 먼저 associativity는 순서와 관련된 성질로, $\mathfrak{gh}$를 먼저 구하고 $\mathfrak{f}$을 나중에 구하나, 반대로 $\mathfrak{hf}$를 먼저 구하고 $\mathfrak{g}$를 나중에 구하나 결과는 같아야한다는 것이다. 우리가 object를 보존하는 transformation을 이야기하고 있기 때문에 identity를 만족하는 성질은 항상 만족해야 하는 것이다. Identity transformation $\mathfrak{e}$를 곱하는 것이 어떠한 영향도 존재해서는 안되는 것이다. Identity를 보존하는 것이기 때문에 어떠한 정보를 얻거나 잃어서도 안되는 것이다. Inverse transformation을 하여도 group $\mathfrak{G}$에 포함되어야 하고, 마지막으로 두개의 object transformation을 동시에 하더라도 그 결과가 그대로 $\mathfrak{G}$에 포함되어야 할 것이다. 결국 이러한 성질들을 모두 만족해야 group이 될 수 있고, 반대로 group에 해당하는 각 element들은 4가지 성질을 그대로 만족하게 된다.

이러한 transformation은 특정 data 혹은 signal에 대해서 $\mathfrak{g}\cdot x$ 혹은 $\rho(\mathfrak{g})x$ 와 같이 동작하게 되고, 여기서 $\rho(\mathfrak{g})$는 group representation으로 불리게 된다. 각 data에 대해서 group이 존재하는데, 예를 들어 GNN의 경우에는 $\mathfrak{g}$가 permutation이 되고 $x$는 node feature가 될 것이다. 여기서 node feature에 대해서 group representation $\rho(\cdot)$은 permutation matrix가 되는 것이다. $x$가 adjacency matrix가 된다면 $\rho(\cdot)$은 다르게 정의될 것이다. $\rho(\cdot)$는 결국 특정 data에 맞는 transformation이 될 것이다. 예를 들어, 정말 유명한 symmetry로 rotation symmetry를 생각해보자. 32x32 크기 혹인 256x256 크기의 image에 대해서 서로 다른 linear operator가 존재할 것이다. 아무래도 input data의 dimension이 다르기 때문에 서로 다른 $\rho(\cdot)$가 정의될 것이다.

Permutation Group and Symmetry

이번에는 가장 유면한 group과 symmetry로 permutation에 대해서 알아보고자 한다. 또한 우리가 지금 초점을 두고 있는 것이 GNN이기 때문에 여기에 대응되는 permutation은 우리에게 반드시 필요한 내용 중 하나이다. 그리고 graph는 매우 symmetric한 object로 이들은 vertex들의 permutation에 대해서 항상 identity를 보존하고 있기에 GNN은 GDL을 설명하는데 있어 가장 적합한 framework이다. 예를 들어, permutation은 vertex 1,2,3,4,5를 3,2,4,5,1 등의 순서로 바꿀 수가 있다. 이는 실제로 permutation matrix에 의해 수행될 수 있다. 여기서 permutation이 다소 추상적인 개념일 수 있다는 것이다. 그래서 group representation은 명시적으로 symmetric을 다룰 수 있는 쉬운 방법을 제공해준다.

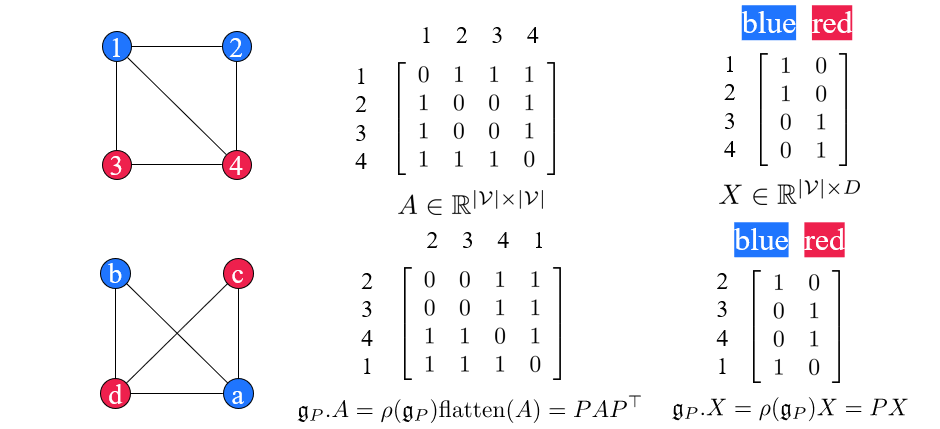간단하게 이해해보기 위해서 1,2,3,4로 구성된 graph가 주어졌다고 해보자. 그리고 이를 설명하는 adjacency matrix와 node feature matrix가 위와 같이 주어졌다. 여기서 하고자하는 것은 permutation symmetry를 실제로 적용해보는 것이다. 우리는 group element $P$를 adjacency matrix $A$에 적용할 것이다. 우리가 permutation을 adjacency에 적용하는 것은 $PAP^T$를 구하는 것과 같다. 그리고 이러한 과정은 $A$를 flatten한 것에 group representation $\rho$를 곱하는 것과 같다. Node feature의 경우에는 간단하게 permutation matrix $P$를 좌측에 곱해주면 된다. 이러한 결과는 동일한 group element $\mathfrak{g}_P$를 가지지만 이들의 group representation $\rho$가 다른 특별한 경우에 해당한다. Adjacency matrix에 대해서는 다소 큰 permutation matrix를 사용해야하지만, node feature matrix에 대해서는 단순히 원래의 permuation matrix를 사용하게 된다. 그래서 representation이 서로 다른 경우에 해당한다.

Invariant Graph Network

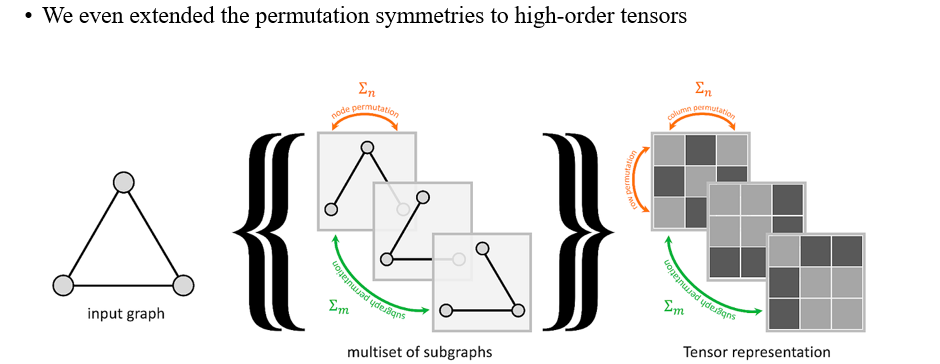이번에는 invariant graph network (IGN)에 대해서 symmetry를 설명하고자 할 것이고, IGN은 여러 subgraph들로 구성될 수 있다. Subgraph는 작은 adjacency matrix로 설명할 수 있으며 이들을 여러개 쌓을 수가 있다. 여러개를 쌓기 때문에 이에 따라 high-order로 여겨지며 column, row, subgraph 관점에서 permutation이 이뤄질 수 있다. 그래서 하나의 column, 하나의 row, 하나의 subgraph에 permutation matrix를 곱할 수 있는 상황이 나오는 것이다. 그렇기 때문에 우리는 permutation symmetry를 high-order tensor로도 확장시킬 수 있는 것이다. IGN 논문을 읽어보면 실제로 group theory와 관련하여 글이 적혀 있기 때문에 밀접한 관련이 있음을 알 수 있다.

1. Invariance and Equivariance

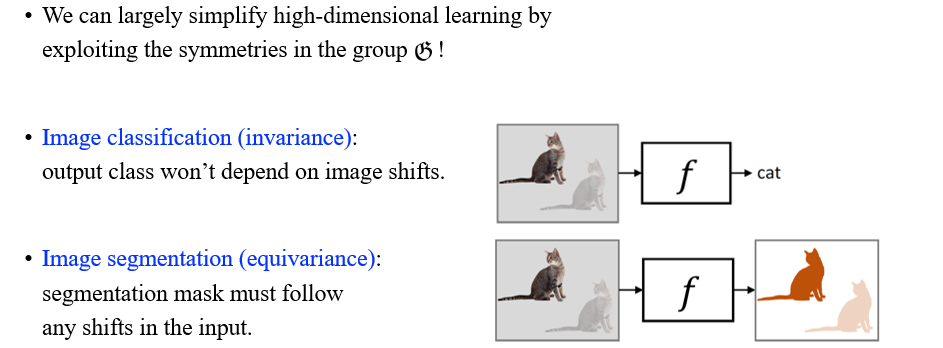Symmetry가 있으면 우리는 black-box function이 요구되는 행동들을 정의할 수 있다. 우리가 cat을 예측해야 한다면, transformation에 따라서 object가 보존되지 않음을 알고 있다. 고양이를 예측하는 것은 image prediction으로 invariance가 강조되는 분야이다. 그러나, segmentation의 경우에는 pixel-wise prediction을 해야하기에 equivariant task에 해당하게 된다. 즉, 고양이가 움직임에 따라서 그 결과도 달라진다는 것이다. 그렇다면 이를 어떻게 수식으로 정리할 수 있을까?

Group symmetry를 적용하는 순서를 바꿈으로써 invariance와 equivariance를 쉽게 정의할 수 있게 된다. Invariance는 data $x$가 있으면 group 혹은 symmetry를 적용했을 때 output이 바뀌면 안된다. 반대로 equivariance는 input에 transformation을 적용했을 때 대응되는 output이 달라져야 한다.

Invariance from Equivariance

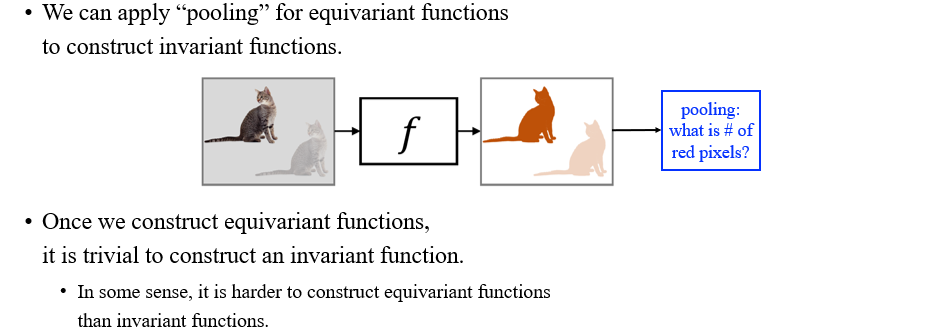Equivraiant function에 pooling을 적용해서 invariant function을 만들 수가 있다. 우리는 equivariant function을 어떻게 만드는지 알기 때문에 invariant function을 만드는 것은 다소 trivial한 것이다. 그렇기 때문에 equivariance가 invariance보다 더 큰 개념으로 생각할 수 있다.

2. Deformation Stability

우리가 지금까지 invariant와 equivariant를 이야기 했으면, 추가적으로 approximately invariant와 equivariant도 이야기해볼 수 있다. Invariance를 이야기 할때마다 우리는 object를 보존하는 transformation 하에서 얼마나 function이 바뀌는지 생각해볼 수 있다. 이로부터 결국 우리는 domain의 약간의 변형에도 안정적인 구조를 설계해야 한다.

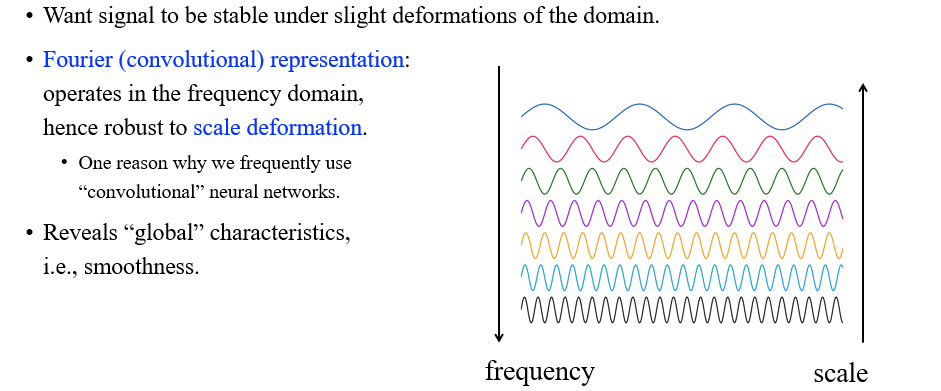사람들은 특정 signal이 약간의 domain 변형에도 안정적이게 만들기 위해서 Fourier representation이라는 개념을 도입하게 되었다. 여기서 Fourier representation이라는 것은 주어진 signal을 여러 signal로 표현하는 것을 이야기한다. 그리고 이들은 scale의 변형에 robust하다. 이것이 의미하는 것은 위에서 red signal이 green signal로 바뀌거나 green signal이 blue signal로 바뀌게 된다면 signal의 변화적인 측면에서는 굉장히 클 것이다. 하지만 Fourier domain에서 그 변화는 굉장히 작다는 것이다. 만약 우리가 이러한 Fourier representation을 사용하게 된다면 scale에서의 변화는 매우 작음을 의미하게 될 것이다.

3. Scale Separation Prior

여기서 우리는 scale speration prior를 가지게 되는데, 이는 data가 주어지게 되면 input의 global하거나 local한 정보 또한 주어진다는 것을 의미한다. 예를 들어, image가 있을 때 바다, 산 등이 있는데 여기에 blur 처리가 되면 이러한 detail들이 smooth해지게 될 것이다. 그럼에도 우리는 흐릿한 image에서도 산과 바다가 있다는 것 정도는 파악할 수 있게 된다. 이러한 identity를 coarse scael dominate라고 하는 것이고, 이는 global context에 해당하게 된다. 반대로 가끔은 local한 정보가 필요할 때도 있을 것이다. Image의 texture를 분류해야하는 문제를 풀 때 blur가 된다면 texture를 파악할 수 없을 것이다.

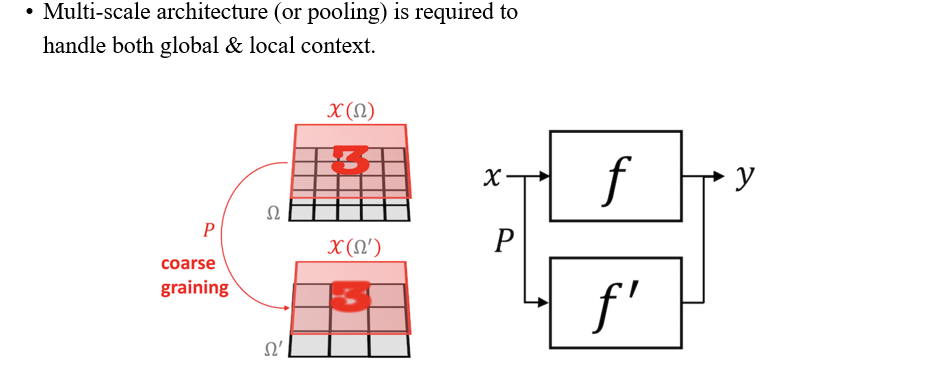만약 우리가 global & local context를 모두 필요하게 된다면 우리는 pooling으로부터 좋은 아이디어를 얻을 수가 있다. 우리는 어떤 signal이 있을 때 coarse graining 방식으로 이를 transformation을 시킬 수 있고, 이로부터 global하고 local한 정보를 동시에 처리해볼 수 있게 된다.

Summary: Blueprint for Geometric Deep Learning

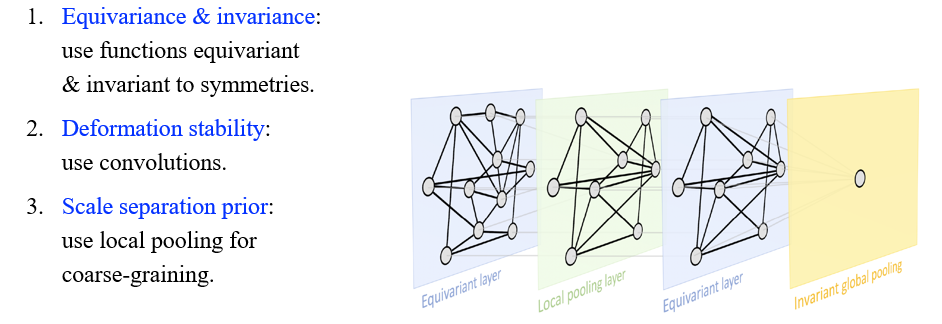요약하면 만약 equivariance와 invariance를 가지고 있다면 symmetry에다가 특정 function을 적용해볼 수 있을 것이다. 만약 deformation stability를 가지고 있다면 approximately equivariant function을 적용해볼 수 있을 것이고, 대표적인 것이 convolution이다. 마지막으로 scale speration prior를 가지고 있다면 우리가 local & global context를 얻기 위해서 pooling operation 등을 적용해볼 수 있을 것이다. 사람들은 이와 같이 3가지 요구사항들을 GDL에서 필요한 요소들로 생각하고 있으며, 어떠한 deep learning 구조에서도 이러한 부분들을 설명할 수 있어야 한다. GNN에서는 equivariance와 invariance는 이미 집중적으로 연구가 되고 있으며 이 부분이 정말 중요한 것을 알 수가 있다.