1) 탐색 알고리즘 이란, 데이터베이스 속 타겟값을 탐색하는 알고리즘을 말한다.

흔히 사용되는 탐색 알고리즘은 다음과 같이 무수히 많다.

1. 선형 탐색
2. 이진 탐색
3. 해시 테이블
4. 이진 탐색 트리
   ....

위와 같은 모든 탐색 알고리즘의 최악의 경우 시간복잡도는 O(n) 보다 효율적일 수 없다.
계속 타겟값이 안 나오는 경우엔 마지막에 있는 원소까지 다 확인해봐야하기 때문이다.

....최소한, 고전적인 컴퓨터로는 말이다

2) 양자 컴퓨팅 은, 일반적인 Bit가 아닌 Qubit으로 알고리즘을 수행하는 방법이다.

• Qubit : 퀀텀 비트라고 불리며, 0 혹은 1 중 하나의 값만 가질 수 있는 Bit와 달리, 0과 1의 상태를 동시에 중첩되게 가질 수 있다.

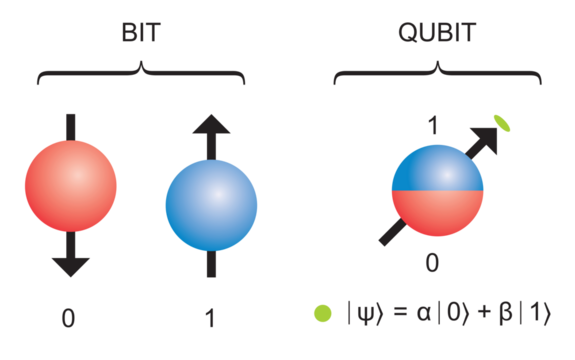
여기서 큐빗의 α 와 β는 확률 진폭으로, 큐빗을 측정했을 때 0이 측정될 확률이 |α|^2, 1이 측정될 확률은 |β|^2 이다. (|α|^2 + |β|^2 = 1)

• 양자 컴퓨팅에 대한 가장 큰 오해는, 큐빗이 0과 1의 값을 동시에 저장하고 사용한다는 것인데, 이는 옳지 않다.
  동시에 값을 갖는 것이 아닌, 각 값을 가질 확률 0부터 1 사이인 것이고, 실제 측정하면 하나의 값만 튀어나온다.

하지만 이러한 중첩성을 잘 이용하면 고전적인 컴퓨터보다 훨씬 빠르게 작동하는 알고리즘을 만들 수 있다.

3) 그로버 알고리즘

• 그로버 알고리즘은, 양자 중첩성을 사용해 O(√n)의 시간 복잡도 로 정렬되지 않은 데이터베이스 속 타겟값을 찾는 알고리즘이다.

타겟값을 향한 확률 진폭 확대(Amplitude Amplification) 을 실행해, 큐빗을 측정했을 때, 타겟값을 관측하게 만드는 확률을 높인다.

그런데 여기서 의아한 점은, 타겟값을 관측하게 만드는 확률?....
아쉽게도 양자
측정의 특성상, 모든 조건을 완벽하게 갖춰도 타겟값을 도출할 확률은 절대 100%가 되지 않는다.

하지만 데이터베이스 크기 n에 대해 약 √n번의 확률 진폭 확대를 실행하면, 타겟값 도출 확률은 100%에 아주 가깝게 수렴한다.

확률 진폭 확대의 특성상, √n번 보다 더 많이 실행할 경우 타겟값 도출 확률은 다시 줄어든다.

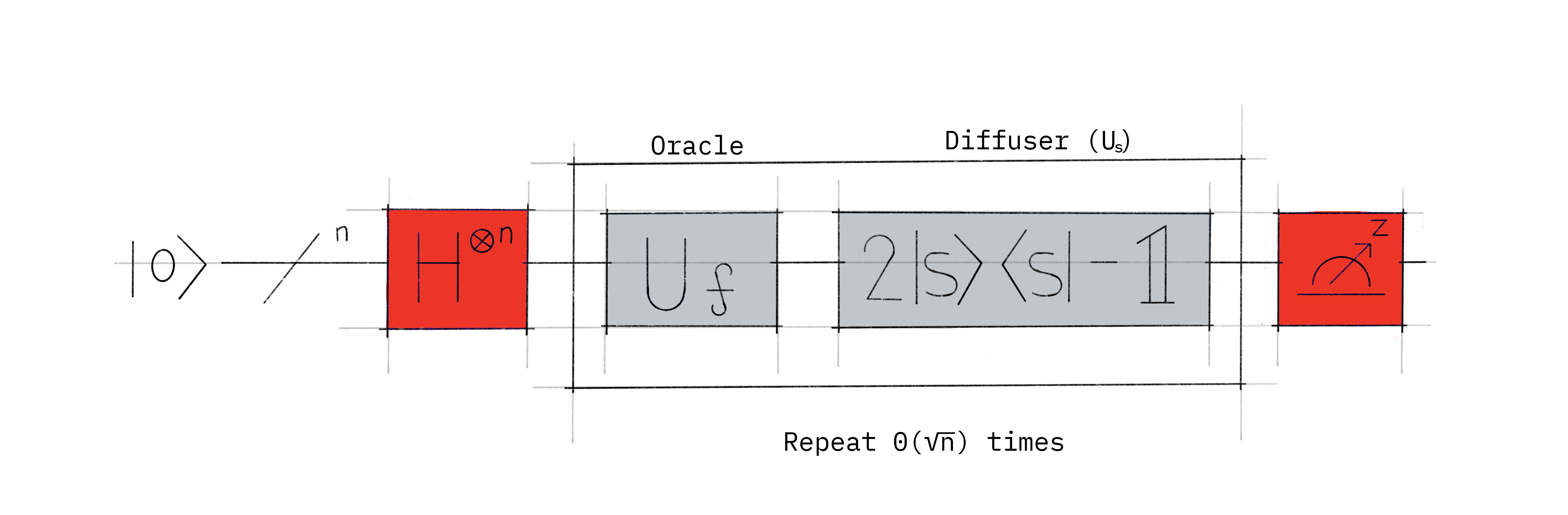
위 그림은 그로버 알고리즘을 나타낸 양자 회로로,

• 첫 빨간색 박스는 모든 원소 값을 양자 중첩화 시킨다.
• 중간 흰색 박스가 Oracle과 Diffuser로 이루어진 확률 진폭 확대 단계 이다.

흰색 박스를 √n번 반복한 후, 마지막에 관측을 하면 타겟값을 도출할 수 있다.

4) Python Implementation

Grover's algorithm을 실행하기 위해서는 양자 컴퓨터가 필요하다.

실제로 IBMQ라는 모듈을 사용하면 IBM의 양자 컴퓨터를 빌려 쓸 수 있는데, 돌려본 결과

이 화면에서 4시간동안 넘어가질 않는다... 트래픽이 그렇게 많은가..?

그래서 양자 컴퓨터의 시뮬레이션 버전인 qiskit를 사용해서 Jupyter Notebook 에서 알고리즘을 돌려보자.

1. 필요 모듈 다운로드

pip install qiskit

2. 필요 모듈 Import

from qiskit import Aer, QuantumCircuit, execute
from qiskit.visualization import plot_histogram

예시로 2-Qubit 데이터베이스 (00, 01, 10, 11) 에서 11을 타겟값으로 설정하고 실행해보자.

3. 2-Qubit 데이터베이스 초기화

def Initialize(QC, Qubits):
    for q in Qubits:
        QC.h(q)
    return QC

4. 2-Qubit 양자 중첩화

n = 2
grover_circuit = QuantumCircuit(n)
grover_circuit = Initialize(grover_circuit, [0,1])

위 서킷을 draw 하면 다음과 같다.

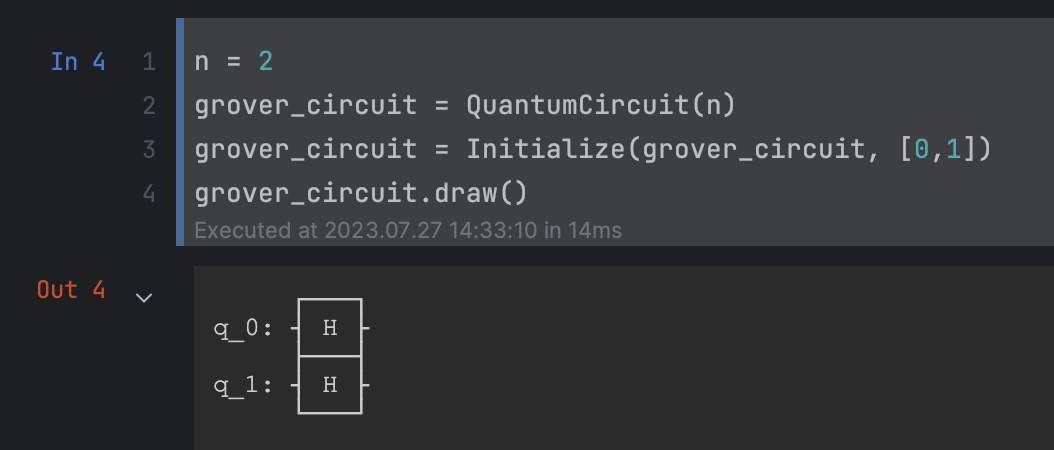
5. Oracle & Diffuser 추가

# Add Oracle Matrix
grover_circuit.cz(0,1)

# Add Diffuser
grover_circuit.h([0,1])
grover_circuit.z([0,1])
grover_circuit.cz(0,1)
grover_circuit.h([0,1])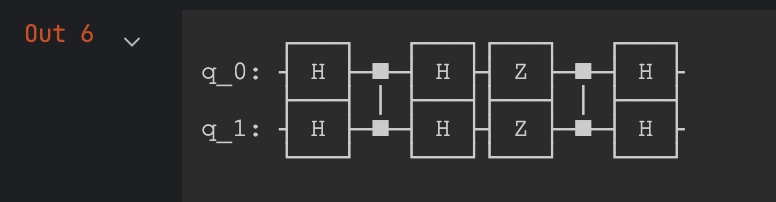

6. Circuit Simulation & Qubit 측정

# Simulate the Circuit
sv_sim = Aer.get_backend('statevector_simulator')
job_sim = execute(grover_circuit, sv_sim)
statevec = job_sim.result().get_statevector()

# Measure the Qubits
grover_circuit.measure_all()

qasm_simulator = Aer.get_backend('qasm_simulator')
shots = 1024
results = execute(grover_circuit, backend=qasm_simulator, shots=shots).result()
answer = results.get_counts()
plot_histogram(answer)

여기서 Shots는 실제 이 실험을 1024번 실행해 몇 번 타겟값을 측정하는지, 즉 타겟값 도출 확률을 구하는 것이다.

결과는 다음과 같이 1024번 모두 타겟값인 11을 도출했다.

이 코드는 실제 양자 컴퓨터가 아닌 시뮬레이션이기 때문에 오차값을 배제하고 답만 도출해서 확률이 100%이다.

실제 양자 컴퓨터로 시뮬레이션을 돌리면 정답 측정이 다음과 같이 나온다.

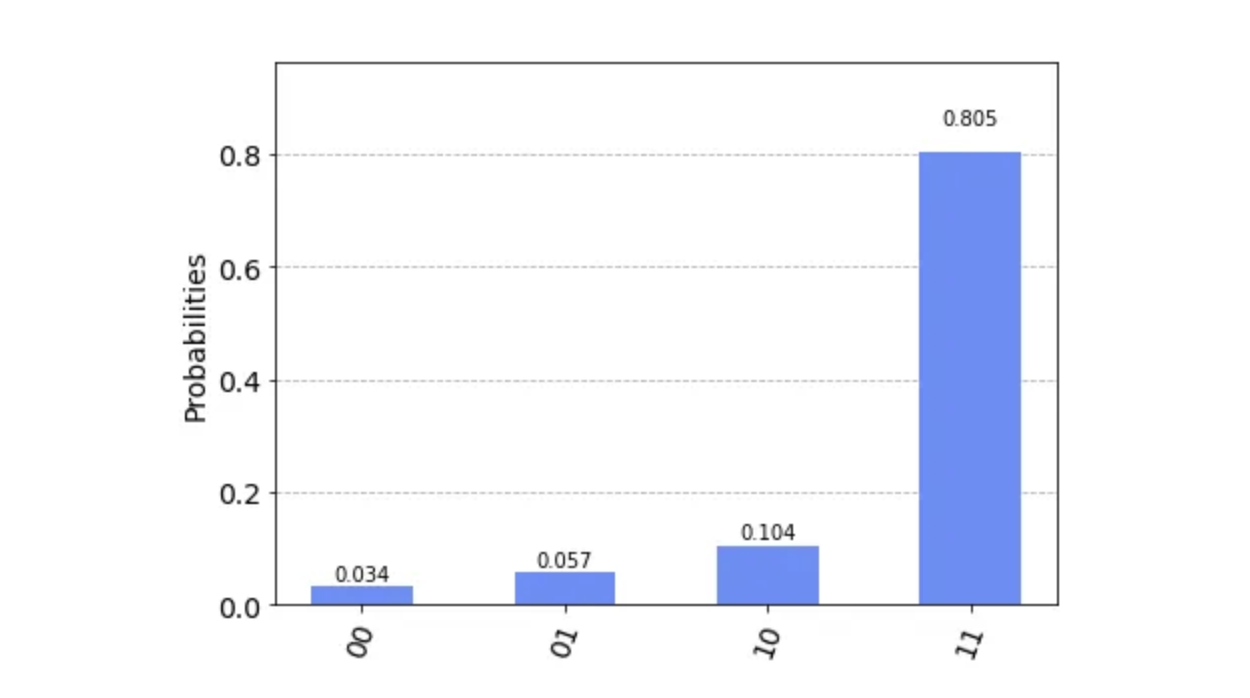
• 결론적으로, 그로버 알고리즘은 n개의 원소를 가진 데이터베이스에 대해 확률 진폭 확대 단계를 √n번 실행하면, 100%에 수렴하는 확률로 타겟값을 도출할 수 있다. (실제로 √n번이 아니라 경우마다 √n의 실수배일 수 있다.)

결국 이 탐색 알고리즘의 시간복잡도는 최악의 경우 O(√n)이다.

5) 실제 양자 컴퓨터로 실행해보기

시뮬레이션이 아닌, 실제 IBM의 양자 컴퓨터를 빌려와 코드를 돌려볼 수 있다.
API KEY 발급같이 번거로운 과정 없이도 아래 코드를 실행하면 된다!

from qiskit import QuantumCircuit, transpile
from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2
import matplotlib.pyplot as plt

service = QiskitRuntimeService()

backend = service.least_busy(simulator=False, operational=True, min_num_qubits=3)
print(f"Running on: {backend.name}")

n = 2
qc = QuantumCircuit(n)
qc.h(range(n))
qc.cz(0, 1)
qc.h(range(n))
qc.z(range(n))
qc.cz(0, 1)
qc.h(range(n))
qc.measure_all()

qc_t = transpile(qc, backend=backend, optimization_level=3)

sampler = SamplerV2(backend)
job = sampler.run([qc_t], shots=1024)
job.wait_for_final_state()

result = job.result()[0]
counts = result.join_data().get_counts()

all_keys = ['00', '01', '10', '11']
values = [counts.get(k, 0) for k in all_keys]

total_shots = sum(values)
probs = [v / total_shots for v in values]
plt.figure(figsize=(8, 5))
bars = plt.bar(all_keys, probs, color='skyblue')

for bar, prob in zip(bars, probs):
    height = bar.get_height()
    plt.text(bar.get_x() + bar.get_width() / 2, height + 0.02, f"{prob:.3f}", ha='center')

plt.xlabel("Measurement Outcome")
plt.ylabel("Probability")
plt.title("Grover's Algorithm Result")
plt.ylim(0, 1.05)
plt.grid(axis='y', linestyle='--', alpha=0.6)
plt.tight_layout()
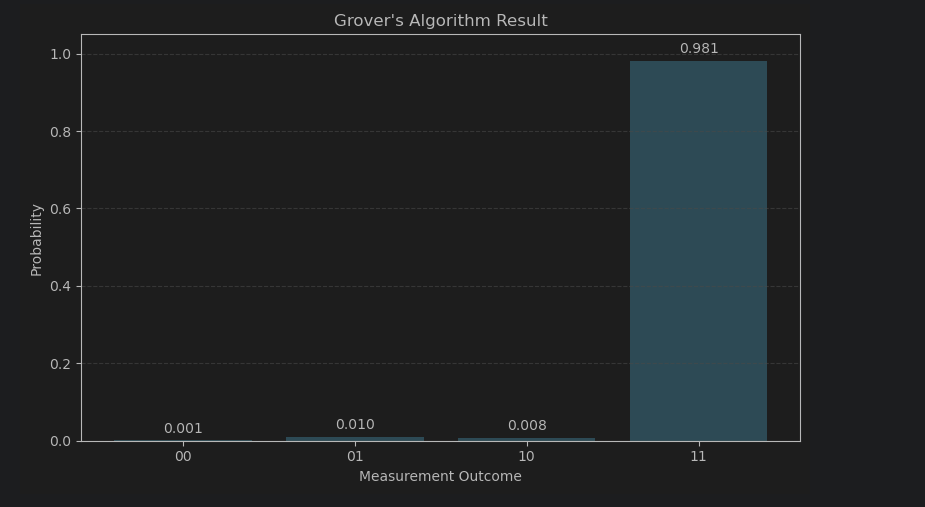
plt.show()

실제 양자컴퓨터에서 그로버 알고리즘 실행 결과