Finite Automata

• 유한한 상태의 집합으로 transition 규칙을 나타낸다.
• transition 규칙은 하나의 상태에서 input을 받고 다른 상태로 넘어가는 것을 말한다.
• 디지털 회로 설계를 위한 소프트웨어, 컴파일러의 lexical analyzer, 파일이나 웹의 키워드 찾는 text editor, communication 프로토콜과 같은 것에 이용된다.

  - on-off 스위치 모델링
  - 영단어 인식
  - vending머신 설계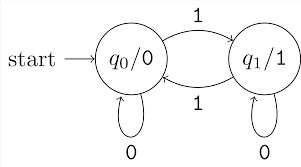

  

Language

Alphabets

문자의 유한집합. 예를 들어 ASCII, Unicode, {0, 1}, {a, b, c} 등이 있다.
$\sum$로 나타낸다.

Strings

알파벳의 모음.
$\sum^*$은 스트링의 집합이다.
$\vert s \vert$는 스트링 s의 길이를 의미한다.
$\epsilon$은 빈 스트링을 의미한다. $\vert \epsilon \vert$ = 0.

예를 들어,
$\{0, 1\}^*$ = $\{\epsilon, 0, 1, 00, 01, 10, 11, 000, 001, ...\}$

Language는 $\sum^*$의 부분집합이다.

DFA (Deterministic finite automata)

• $Q$ : 상태 유한 집합
• $\sum$ : 인풋 알파벳
• $\delta$ : transition 함수
• $q_0$ : 시작 상태
• $F$ : final state 집합

Transition function

두 개의 인자를 갖는다. state와 input symbol.
$\delta(q, a)$ = DFA에서 상태 $q$가 $a$를 받았을 때 가는 상태값

그래프

노드는 상태를 가르킨다.
화살표는 transition function이며 화살표에 쓰여 있는 값이 input symbol(=알파벳)이다.
받는 화살표가 있는 노드가 "start" state.
final state는 동그라미가 두개인 노드이다. 여러개 가능.

• $Q = \{X_0,X_1,X_2,X_3,X_4\}$
• $\sum = \{0, 1\}$
• $\delta(X_0,0) = X_0$
  $\delta(X_0,1) = X_1$
  $\delta(X_1,0) = X_2$
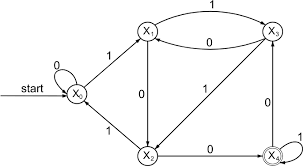
  $\delta(X_1,1) = X_3$ 등등
• $q_0 = X_0$
• $F = \{X_4\}$

테이블

transition table of DFA

State	0	1
$\rarr X_0$	$X_0$	$X_1$
$X_1$	$X_2$	$X_3$
$X_2$	$X_4$	$X_0$
$X_3$	$X_1$	$X_2$
$*\,X_4$	$X_3$	$X_4$

화살표는 start state를 의미하고 *은 final state를 의미한다.

Language of a DFA

• 모든 오토마타는 language를 정의한다.
• A가 automaton이면 L(A)는 language를 의미한다.
• L(A)는 start state에서 final state로 갈 수 있는 input 조합이다.