백준 2293 동전 1

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Coin {

	public static void main(String[] args) throws IOException{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st= new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken());
		int K = Integer.parseInt(st.nextToken());
		int[] arr = new int[N];
		int[] dp = new int[K+1];
		for (int i = 0; i <N ; i++) {
			st = new StringTokenizer(br.readLine());
			arr[i]= Integer.parseInt(st.nextToken()); 
		}
		dp[0] = 1;
		for (int i = 0; i < N; i++) {
			for (int j = arr[i]; j < K+1; j++) {
				if(arr[i]<=j) {
					dp[j] += dp[j-arr[i]];
				}
				
			}
			
		}
		System.out.println(dp[K]); 

	}

}

풀이방법

우선접근 방법이 가장 중요한데, 동전이 1개만 있을때, 2개 있을때, 3개있을때, 이런식으로 경우의 수를 구해야 한다.
하지만 그렇다고 2차원 배열을 쓰면 메모리 초과가 발생하므로, 이전 코인의 dp값을 토대로 다음 코인의 dp값을 구해야한다.

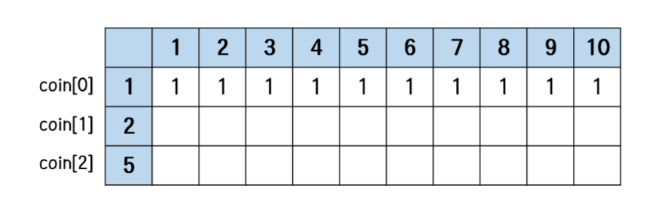
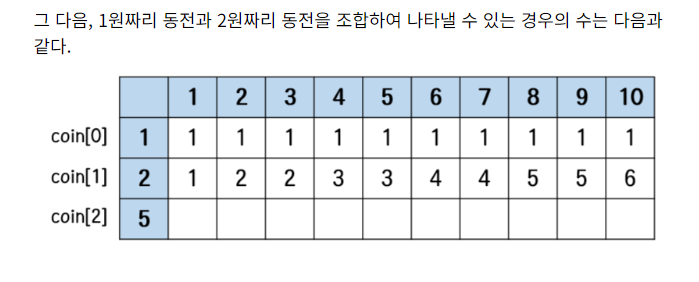
👉여기서 살펴보면 코인이 2개 있을때는, coin[1] >= 코인의 합 일때부터 변화가 생긴다.
k = 3일 때는 어떻게 될까?
기존에 1원짜리 동전만으로 나타냈을 때의 경우의 수는 1이었다. dp[3] = 1
📢3원을 만들기 위해 2원짜리 동전을 사용하는 경우는 k = 1일 때 dp[1]의 경우의 수와 같다.
즉 dp[k-coin[i]] 인것이다.
따라서 기존에 코인 하나만 사용했을때의 경우의 수인 dp[k]값에 dp[k-coin[i]]값을 더해주면된다.

😒여기서 의문, 코인의 값이 1,2,5가 아닌 5,2,1로 들어와도 되나?

질문게시판 참고.

후기

일단 접근법 부터 틀렸다.
같은 코인의 갯수 안에서 dp값을 구하려 했는데
코인이 1개일때, 2개일때로 나눠서 접근해야했다.
이부분이 핵심 포인트였는데, 이걸 어떻게 생각해내야 했을까,, 벽느껴진다.
풀이를 보고 잠깐 순서에 의문이 생겼지만, 이부분은 생각해보니 고려하지 않아도 되는 부분같다.