백준 2133번 타일 채우기

https://www.acmicpc.net/problem/2133

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class FillTile {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        long[] dp = new long[31];
        dp[2] = 3;
        dp[4] = 11;
        for (int i = 6; i < 31; i++) {
            if(i%2==1) continue;
            dp[i] = dp[i-2]*3;
            for (int j = 2; j < i-2; j++) {
                dp[i] += dp[j]*2;
            }
            dp[i] += 2;
        }
        System.out.println(dp[N]);
    }
}

풀이방법

📢 이문제는 점화식을 찾는게 핵심이다. 점화식만 찾으면 풀이는 매우 쉽다.
점화식을 찾기 위해선, 규칙이 보일때까지 노가다로 세주어야 한다.
1. N이 홀수일때는 가능한 경우의 수가 없다.

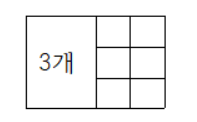
2. N이 2일때는 3

3. N이 4일때는 N이 2일때가 두번 있다고 생각하면 된다. 3x3

🔉하지만 4일때만 나오는 경우의수가 딱 두개가 추가로 생긴다.

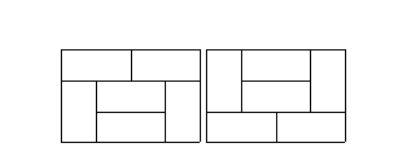
이것을 찾아내는게 핵심이다.
따라서 3x3+2 = 11

4. 계속해서 N이 6일때를 보면
   
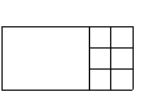
   이런식으로 9 x 3을 해준다.
   🔉그리고 N이 4일때 나온 특수한 모형 2가지 x 3을 해준다.
   
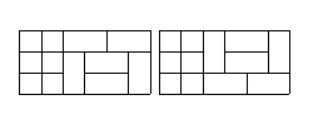
   이후 마찬가지로 N이 6일때 나온 특수한 모형 2가지가 추가로 생긴다.
   따라서 11x3 + 2x3 + 2 = 41

5. 마지막으로 N이 6일때를 살펴보면
   41 x 3 + 2 x 11 + 2 x 3 + 2 = 153이 된다.

6. 👉점화식으로 나타내면
   dp[i] = dp[i-2]x3 + dp[i-4]x2+...+ dp[2]x2 + 2가 된다.

후기

특수한 모형이 2가지 나오는건 찾았는데, 이전에 나온 모든 특수한 모형까지 전부x2 해줘야 하는지 발견 못해서 힘들었다.
이런 찾기 힘든 점화식이 필요할까..