백준 12865번 평범한 배낭

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class NormalBackpack {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int K = Integer.parseInt(st.nextToken());
        int[] W = new int[N+1];
        int[] V = new int[N+1];
        for (int i = 1; i < N+1; i++) {
            st = new StringTokenizer(br.readLine());
            W[i] = Integer.parseInt(st.nextToken());
            V[i] = Integer.parseInt(st.nextToken());
        }
        int[][] dp = new int[N+1][K+1];//물건의 인덱스별, 무게별 가치. 같은 무게여도, 다른 인덱스 일수도 있어서
        for (int i = 1; i < N+1; i++) {
            for (int j = 1; j < K+1; j++) {
                if(j-W[i]>=0){
                    dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-W[i]]+V[i]);
                }
                else {
                    dp[i][j] = dp[i-1][j];
                }

            }
        }
        System.out.println(dp[N][K]);

    }
}

풀이방법

우선 dp배열에 들어가야할 값은, 물건의 인덱스별 무게별 가치합이 들어가야한다.
그냥 무게별 가치합으로 일차원 배열로 설정한다면, 같은 무게인데 다른 물건으로 이루어졌을때, 관계정립을 할 수가 없다.
따라서 물건의 인덱스별 무게별 가치합, 이차원 배열을 통해 dp를 설정한다.

해당 dp 배열을 순차적으로 채워 넣는다.

인덱스 1일때, 물건은 6, 13 이다.
즉 6 미만의 무게는 들어갈수가 없다.
이런식으로 물건을 가방에 넣을 수 있다면, 해당 dp배열에 가치값을 넣어준다.
이때, 해당 인덱스의 물건을 안넣어야 최대일 수도 있다.

따라서

if(j-W[i]>=0){
        dp[i][j] = Math.max(dp[i-1][j],V[i]);
}

이렇게 된다.
하지만, 물건을 여러개 넣은 가치합이 최대인 경우는 고려하지 않았다.

물건의 합을 고려한다면, dp[i-1][j-W[i]]+V[i] 이다.
'이전 인덱스(현재 인덱스의 무게를 뺀)의 가치값 + 현재 인덱스의 가치값'을 통해 물건 여러개 넣은 가치합을 고려하여 dp를 갱신한다.

if(j-W[i]>=0){
        dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-W[i]]+V[i]);
}

이때, 현재 무게에서는 물건을 넣을 수 없었지만, 이후 탐색하는 무게가 증가함에 따라 현재 dp에서의 물건을 참조해야하는 경우가 있다.

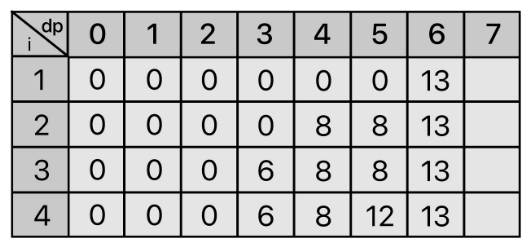
(4,3)(4,4)에서는 사실 4번째 인덱스는 무게가 5이므로 0이 들어가야 한다.
하지만 추후 dp[i-1][j-W[i]]+V[i] 을 통해 dp[4][3]+V[5]를 해야 할 수도 있다.
따라서 물건에 넣을 수 없는 경우에는 이전 인덱스의 dp값을 넣어준다.
즉 ~인덱스 까지 탐색한다는 누적합 개념으로 설정하는 것이다.

if(j-W[i]>=0){
		dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-W[i]]+V[i]);
}
else {
        dp[i][j] = dp[i-1][j];
}

마지막에 dp[N][K] 값을 출력한다.

후기

이차원 배열의 dp였는데, if문 구상이 너무 어려운데다가, 누적합으로 생각했어야 하는 점이 복잡했다.