백준 101번 다리놓기

1번 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class PutBridge {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int T = Integer.parseInt(st.nextToken());
        for (int test = 0; test < T; test++) {
            st = new StringTokenizer(br.readLine());
            int N = Integer.parseInt(st.nextToken());
            int M = Integer.parseInt(st.nextToken());
            long answer = 1;
            if(N>M/2){
                N = M-N;
            }
            for (int i = 0; i < N; i++) {
                answer = answer*(M-i);
            }
            for (int i = 1; i <= N; i++) {
                answer = answer/i;
            }
            System.out.println(answer);
        }
    }
}

풀이방법

nCr의 조합을 사용하면 된다까지는 확인할 수 있다.
다만 nCr을 어떻게 구현할 것인가가 문제이다.

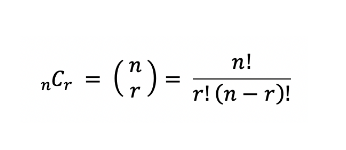
이를 그대로 구현하면, long 자료형에 29!을 담을 수가 없다.
따라서 약분한 식을 구현해준다.
즉, 7C4 라면, 7x6x5x4 / 4x3x2x1 의 형태로 구현한다.
하지만 이렇게 수행해도 여전히 약분이 안되는 조합은 long형에 담을 수 없다.

여기서 nCr = nCn-r 공식을 사용한다.
즉, 최대한 약분이 될 수 있는 형태를 만들어 사용하는 것이다.
예를 들면, 29C28는 29!/28!을 수행해야 하는데, 공식을 통해 29C1을 대신 수행하도록 하는것이다.
이렇게 만들면 long형 범위에 들어가고, 테스트케이스를 통과한다.

2번 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class PutBridge {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int T = Integer.parseInt(st.nextToken());
        for (int test = 0; test < T; test++) {
            st = new StringTokenizer(br.readLine());
            int N = Integer.parseInt(st.nextToken());
            int M = Integer.parseInt(st.nextToken());
            int[][] dp = new int[30][30];
            for (int i = 0; i <= M; i++) {
                dp[i][0] = 1;
            }
            for (int i = 1; i <= M; i++) {
                for (int j = 1; j <= N; j++) {
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
                }
            }
            System.out.println(dp[M][N]);
        }
    }
}

풀이방법

2번째 풀이는 dp를 사용하는 정석적인 풀이이다.
이문제에 dp를 사용하기 위해 알아야할 전제 조건은

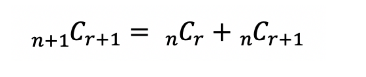
이 공식이다.
파스칼의 법칙이라고 불린다.
N을 열, M을 행으로 하는 dp 배열을 통해 파스칼의 법칙을 적용하여 dp배열을 완성해준다.
N,M에 해당하는 dp배열을 출력하면 된다.

후기

난 파스칼의 법칙을 몰라서 dp로 풀지 못했다.
수학공식에 의존한 풀이라고 생각하기는 하지만 유명한 수학공식이라고 하니 알아두자.
공식을 알고 구현하는건 어렵지 않았다.