백준 1003번 피보나치 함수

피보나치 수열

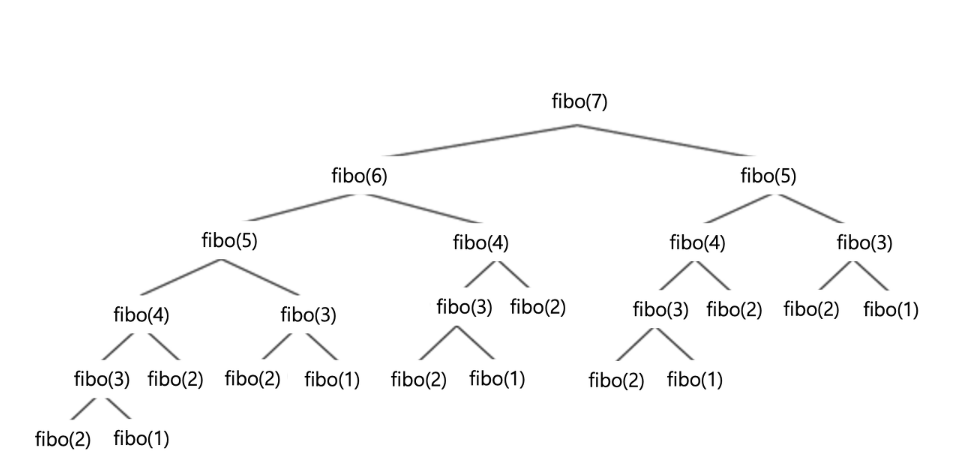
👉 7번째 수열을 찾으려면 여러개의 이전 순열의 조합을 통해 찾게 된다.
이과정에서 fibo(1), fibo(0)의 함수처럼 가장 말단의 함수는 매우 많은 호출을 수행하게 된다.
👉피보나치 수열 0 1 1 2 3 5 8 에서
f(0) = 8번 호출
f(1), f(2) = 5번 호출
f(3) = 3번 호출
f(4) = 2번 호출
f(5) = 1번 호출
f(6) = 1번 호출
호출 횟수도 피보나치 수열을 따르는 것을 확인할 수 있다.
따라서 0번과 1번의 호출횟수를 구하는 문제라면, 수열의 맨끝값, 바로전값을 구하면 된다.

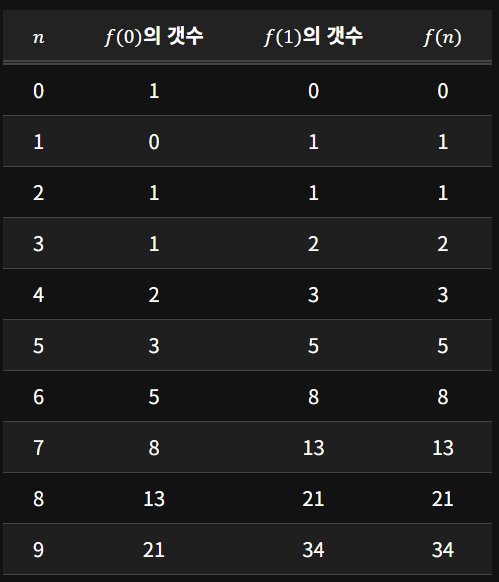
따라서 한번 호출해서 값을 저장한다면, 호출을 여러번 수행하는 대신, 저장된 값을 가져다 써서 더 효율적으로 사용할 수 있다.

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Fibonacci2 {
    static int[] dp;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int T = Integer.parseInt(st.nextToken());
        for (int i = 0; i < T; i++) {
            st = new StringTokenizer(br.readLine());
            int N = Integer.parseInt(st.nextToken());
            dp = new int[N+1];
            fibonacci(N);
            if(N == 0){
                System.out.println(1+" "+0);
            }
            else {
                System.out.println(dp[N-1]+" "+dp[N]);
            }

        }
    }
    public static int fibonacci(int n){
        if(n ==0){
            dp[0] = 0;
        }
        else if(n==1){
            dp[1] = 1;
        }
        else if(dp[n]==0){
            dp[n] = fibonacci(n-1)+fibonacci(n-2);
        }
        return dp[n];
    }
}

풀이방법

dp[n] = fibonacci(n-1)+fibonacci(n-2);

이코드에서 이전 순열을 계속 호출하는데,
dp[n] == 0일때, 즉 값이 없을때, 처음 호출하는 수열일때만, 호출을 수행하고, 값이 있을때는 기존에 저장된 수를 가져다 쓴다.

후기

dp입문용 문제로 dp의 기본 개념인 저장하고 그값을 가져다 쓰는것을 사용한다.