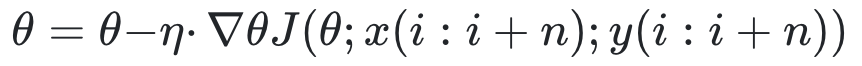temp

$Taille_1 = size(Trainset) * 2,50$
$Taille_2 = size(Trainset) * 3,75$
$Taille_3 = size(Trainset) * 5,00$
$Le \space nombre \space maximum \space de \space données \space à \space ajouter \space est \space de \space 6 \space 000$

$Taille_1$

$θ = θ − η · ∇θJ(θ)$

$θ = θ − η · ∇θJ(θ; \space x (i:i+n); \space y (i:i+n))$

$hθ(x) = θ_0, θ_1$

$Minimize \space J(θ)$

$R(θ) = Repeat \space until \space convergence \space \lbrace θ = θ − η · ∇θJ(θ) \rbrace$

$θ ∈ R^d$

$f(x)=max(0,x)$

$f(α,x)=max(αx, \space x) ; \space a=0,001 (en \space général)$

$f(α,x)=max(αx, \space x) ; \space a=un \space paramètre \space adjustable$

$θ_{final} = update(\space…\space update\space(\space update\space(\space update(\space θ_{init}\space)\space)\space)\space)$

$Contexte(trainDataset) \approx Contexte(trainDataset_{prime})$

$Minimize(J(θ))\space à\space 1er\space minimum\space local \approx Minimize(J’(θ))\space à\space 1er\space minimum\space local$

$θ_{minima_1} = update(…(update(θ_{init})))$
$\space\space\space\space\space\space\space\space\space\space\spaceθ_{minima_1} \larr shockData$

$θ_{minima_2} = update(…(update(θ_{minima_1})))$
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space\spaceθ_{minima_2} \larr shockData$
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space...$

$θ_{final} = update(…(update(θ_{minima_{n-1}}))); \space Max(final) = n$

$Fournisseur(Data = validDataset, nChoc = c ; 0 <= c <= len(validDataset))$
$\space$ $\space$ $\space$ $Choc \larr Data[: nChoc]$
$\space$ $\space$ $\space$ $Data \larr Data[nChoc:]$

$\space$ $\space$ $\space$ $return \space (Choc,\space Data)$

$Train(N = (θ_init, L), E = epoch, D = (train, valid), C = nChoc, P = patience)$
$\space$ $\space$ $\space$ $e \larr 1$
$\space$ $\space$ $\space$ $p \larr 0$
$\space$ $\space$ $\space$ $minLoss \larr 10^6$
$\space$ $\space$ $\space$ while $\space$ $e\space<E$ $\space$ do
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $tOutput = N(train.data)$
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $tLoss = criterion(tOutput, train.label)$
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $tLoss.backwards()$
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $optimizer.step()$

$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $vOutput = N(valid.data)$
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $vLoss = criterion(vOutput, valid.label)$
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ if $\space$ $vLoss < minLoss$ $\space$ do
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $minLoss \larr vLoss$
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ else
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ if $\space$ $(length(valid.data) > 0)$ $\space$ do
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ if $\space$ $(p == P)$ $\space$ do
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $Choc, \space valid \larr Fournisseur(valid, \space C)$
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $train.data \larr train.data.append(Choc.data)$
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $train.label \larr train.label.append(Choc.label)$
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $p \larr 0$
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ else
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $p \larr p+1$
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $e \larr e+1$

$ForceDirected(G = (V, E), p_{init} = (p_v) v\in V, \varepsilon > 0, K \in N)$

$\space$ $\space$ $\space$ $t \larr 1$

$\space$ $\space$ $\space$ while $t$ $< K$ $and$ $max$$(v\in V)$$||F_v(t)||>\varepsilon$ do
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ foreach $u \in V$ do
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$$\space$ $F_v(t)\larr\sum f_{repulsion}(u, v)+\sum f_{attraction}(u, v)$
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ foreach $u \in V$ do
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $\space$$\space$ $p_u \larr p_u + Accéleration(F_u(t))$
$\space$ $\space$ $\space$ $\space$ $\space$ $\space$ $t \larr t+1$
return $p_{fin}$

Paramètres
$V$ : Vertex (Nœud)
$E$ : Edges
$\varepsilon$ : threshold
$K$ : max itérations
$p_{init}$ : layout initial
$p_{fin}$ : layout à la fin

LinRepulsion

$f_{repulsion}(u,v)=$ $c_{rep}$ $(Deg(v)+1) * (Deg(u)+1) \over {||p_v - p_u||}^2$ . $\overrightarrow{p_vp_u}$

$(1)$ $f_{attraction}(u,v)=$ ${c_{attraction} . ||p_v - p_u||}$ . $\overrightarrow{p_up_v}$

$(2)$ $f_{attraction}(u,v)=$ ${c_{attraction} . log(1 + ||p_v - p_u||})$ . $\overrightarrow{p_up_v}$

Eades

$f_{repulsion}(u,v)=$ $c_{rep} \over {||p_v - p_u||}^2$ . $\overrightarrow{p_vp_u}$

$f_{spring}(u,v)=$ $c_{spring}$ . $log$ ${||p_v - p_u||} \over l$ . $\overrightarrow{p_up_v}$

$f_{attraction}(u,v)=f_{spring}(u,v)-f_{rep}(u,v)$

$F_u = \sum_{v\in V} f_{repulsion}(u,v) + \sum_{uv\in E} f_{attraction}(u,v)$

$||p_u - p_v||$ : Euclidean distance entre u et v
$\overrightarrow{p_up_v}$ : unit vecteur pointant de u à v
$l$ : une longueur idéale des arêtes.
$c$ : une constante

FR

$f_{repulsion}(u,v)=$ $l^2 \over {||p_v - p_u||}$ . $\overrightarrow{p_vp_u}$

$f_{attraction}(u,v)=$ ${||p_v - p_u||^2} \over l$ . $\overrightarrow{p_up_v}$

$F_u = \sum_{v\in V} f_{repulsion}(u,v) + \sum_{uv\in E} f_{attraction}(u,v)$