(작성 중)[C++/자료구조] 합집합 찾기(Union-Find)

1. Union-Find란?

• Union-Find(합집합 찾기) 는 그룹 분할을 효율적으로 관리하는 자료 구조로, 다음과 같은 쿼리를 빠르게 처리한다.
• 루트 트리 구조를 이용한다.
• 크리스컬 알고리즘도 Union-Find를 효과적으로 활용한다.

  • $issame(x, y)$ :: = 요소 $x, y$ 가 같은 그룹에 속하는지 여부를 조사한다.
  • $unite(x, y)$ ::= 요소 $x$ 를 포함한 그룹과 요소 $y$ 를 포함한 그룹끼리 합침

2. Union-Find 구조

Union-Find는 그룹 하나하나가 루트 트리를 구성함으로써 실현할 수 있으며 힙이나 이진 탐색 트리와 다르게 이진 트리일 필요가 없다.
우선 다음과 같이 함수 $root(x)$를 만든다.

Union-Find의 root 함수
$root(x)$ : 요소 $x$ 를 포함하는 그룹(루트 트리)의 루트를 반환한다.

이 root 함수를 이용하면, 각 쿼리의 처리를 다음과 같이 할 수 있다.

쿼리	실현 방법
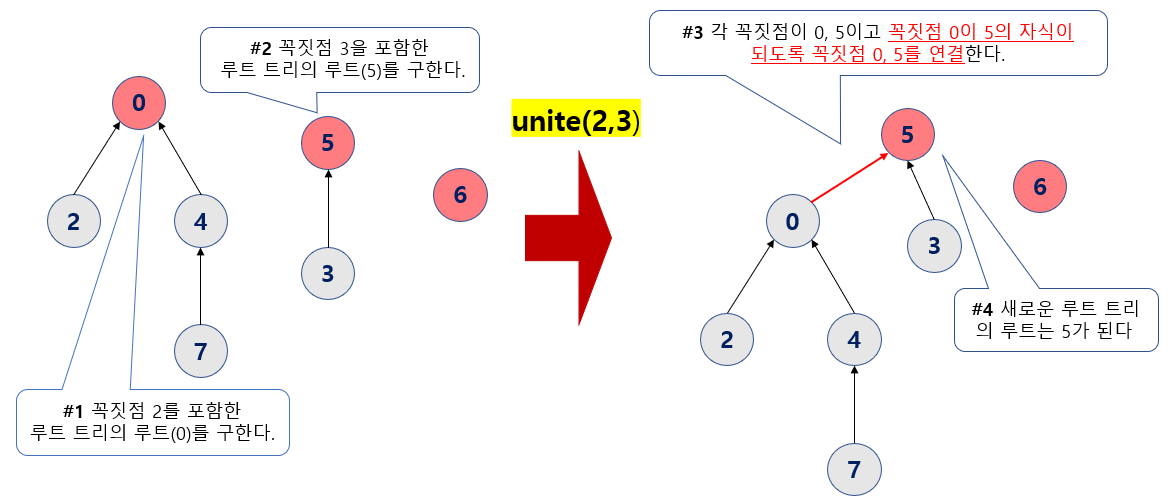
$issame(x,y)$	$root(x)$와 $root(y)$가 같은지 여부를 판단함.
$unite(x,y)$	$r_x = root(x)$, $r_y=root(y)$로 해서 꼭짓점 $r_x$ 가 $r_y$ 의 자식 꼭짓점이 되도록 연결한다.

3. Union-Find의 복잡도를 줄이는 법

Union-Find 쿼리 처리의 핵심은 각 꼭짓점 $x$에 대해 $root(x)$를 구하는 처리가 핵심이다. 각 쿼리의 복잡도는 루트 트리의 높이를 $b$라고 했을 때 $O(b)$가 된다.
$b$는 최대가 $N-1$ 이므로 $O(N)$이 이 되고 상당히 비효율적이다. 따라서 다음 2가지의 개선법을 이용하여 빠르게 처리해보자.

• union by size(union by rank)
• 경로 압축