[C++/자료구조] 그래프(Graph)

1. 그래프(Graph)란?

• 객체 간의 연결 관계를 표현할 수 있는 자료 구조
  
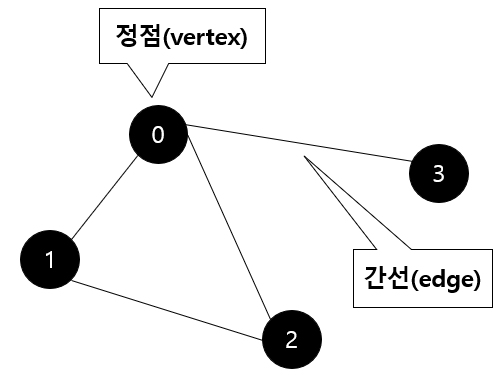
  이 그래프는 다음과 같이 집합으로 표현할 수 있다.

  V(G1) = { 0, 1, 2, 3 }
  E(G1) = { (0,1) , (0,2), (0,3), (1,2) }

++ 간선에 가중치를 부여하게 되면, 간선의 역할이 두 정점간의 연결 유무 뿐만 아니라 연결 강도까지 나타낼 수 있으므로 보다 복잡한 관계를 표현할 수 있게 된다. 따라서 가중치 그래프(weighted graph)를 네트워크(Network)라고도 한다.

• 정점의 차수: 그래프에서 인접한 정점의 수
• 무방향 그래프에서 모든 정점의 차수를 합하면 간선 수의 2배가 된다.
• 방향 그래프에서는 외부에서 오는 간선의 개수를 진입 차수(in-degree), 외부로 향하는 간선의 개수를 진출 차수(out-degree)라고 한다.

1) 그래프의 추상 데이터 타입(ADT)

• 객체: 정점의 집합과 간선의 집합
• 연산:
  create_graph() ::= 그래프를 생성한다.
  init(g) ::= 그래프를 초기화한다.
  insert_vertex(g, v) ::= 그래프 g에 정점 v를 삽입한다.
  insert_edge(g, u, v) ::= 그래프 g에 간선 (u,v)를 삽입한다.
  delete_vertex(g, v) ::= 그래프 g의 정점 v를 삭제한다.
  delete_edge(g, u, v) ::= 그래프 g의 간선 (u,v)를 삭제한다.
  is_empty(g) ::= 그래프 g가 공백 상태인지 확인한다.
  adjacent(v) ::= 정점 v에 인접한 정점들의 리스트를 반환한다.
  destroy_graph(g) ::= 그래프 g를 제거한다.

2) 그래프의 표현 방법

• 인접 행렬(adjacency matrix)
  : 2차원 배열을 이용하여 그래프를 표현한다.
• 인접 리스트(adjacency list)
  : 연결 리스트를 사용하는 그래프를 표현한다.

3) 인접 행렬(adjacency matrix)의 방법

• 그래프의 정점의 수가 $n$이라면, $n*n$ 2차원 배열인 인접 행렬(adjacency matrix) $M$의 각 원소를 다음의 규칙에 의해 할당함으로써 그래프를 메모리에 표현할 수 있다.

if(간선 i, j가 그래프에 존재) M[i][j] = 1
otherwise M[i][j] = 0

그러나, 그래프를 표현할 때는 인접 행렬의 방법보다는 인접 리스트의 방법을 일반적으로 더 많이 이용한다.

4) 인접 리스트(adjacency list)의 방법

• 인접 리스트는 그래프를 표현함에 있어 각각의 정점들에 인접한 정점들을 연결 리스트로 표시한 것이다.

• 

• 

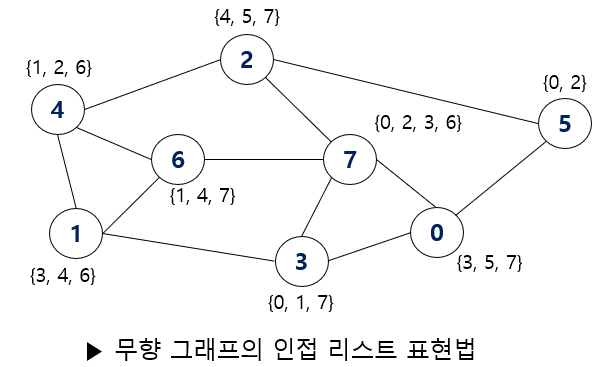
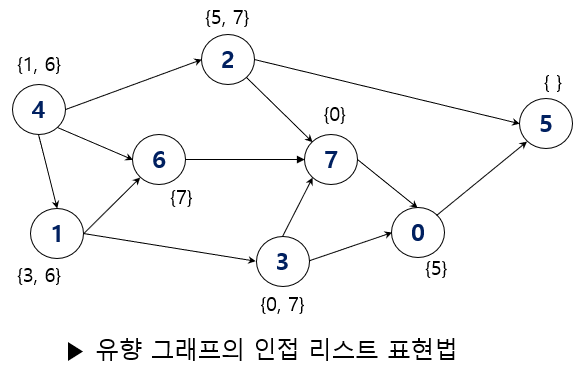
인접 리스트의 표현은 각 정점 v에 대한 인접한 정점 전체를 연결 리스트 구조로 관리하는 것이지만, C++에서는 가변 길이 배열 vector을 이용하면 충분하다.
구체적으로는, 정점 v에 대한 인접 꼭짓점 전체를 $vector<int>$ 형으로 나타낼 수 있다. 그리고 그래프 전체를 $vector<vector<int>>$으로 나타낸다.

using Graph = vector< vector < int >>; // 그래프 형
Graph G; // 그래프

이때 $G[v]$가 $v$의 인접 정점의 집합이다.

G[0] = {5}
G[1] = {3, 6}
G[2] = {5, 7}
G[3] = {0, 7}
G[4] = {1, 2, 6}
G[5] = {}
G[6] = {7}
G[7] = {0}

2. 그래프의 구현

입력 데이터 $N(=정점의 갯수)$ $M(=변의 갯수)$이 차례대로 주어졌을 때,
$i(=0, 1, ... M-1)$번째 변은 정점 $a_i$ 와 $b_i$ 를 연결한다.
이때 유향 그래프라면 $a_i$ 에서 $b_i$ 로 향하는 변을 말하고, 무향 그래프라면 $a_i$ 와 $b_i$를 묶는 변을 말한다.

#include <iostream>
#include <vector>
using namespace std;
using Graph = vector<vector<int>>;

int main() {
	//정점의 갯수와 변의 갯수
	int N, M;
	cin >> N >> M;
	
	//그래프
	Graph G(N);
	for(int i = 0; i < N; ++i) {
          int a, b;
          cin >> a >> b;
		  G[a].push_back(b);

		// 무향 그래프라면 다음 줄을 추가
		// G[b].push_back(a);
	 }
}

1) 가중 그래프(weighted graph) 구현

• 가중치 변을 나타내는 구조체 $Edge$ 사용
• $Edge$ 구조체는 인접 정점의 번호와, 가중치 정보를 멤버변수로 저장한다.
• 비가중 그래프에서는 각 정점 $v$의 인접 리스트 $G[v]$ 가 $v$에 인접하는 정점 번호의 집합을 나타낸다. (→ 최단 경로 문제에서 사용)

#include <iostream>
#include <vector>
using namepsace std;
  
  // 가중치를 나타내는 자료형은 long long형
  struct Edge {
  	int to; //인접 정점의 번호
  	long long w; //가중치
  	Edge(int to, long long w) : to(to), w(w) {}
  };
  
  //각 정점의 인접 리스트를 변 집합으로 나타냄
  using Graph = vector<vector<Edge>>;
  
  int main() {
  	//정점의 개수와 변의 개수
  	int N, M;
  	cin >> N >> M;
  	
  	//그래프
  	Graph G(N);
  	for(int i = 0; i < M; ++i) {
              int a, b;
              long long w;
              cin >> a >> b >> w;
  			  G[a].push_back(Edge(b, w));
  	}
  }