
정리할 게 매우 밀렸는데 이제야 다시 하나씩 해보려고 함... ㅇ<-<
뭐야 벌써 마지막 포스팅 한달 넘게 지났네

종강하면 진짜 열심히 써야지 벨로그 (헛된 다짐)
Morphological Transformation (Binary image)
mathematical morphology는 set theory로 정의된다. 이미지에서 수학적 형태학의 집합(sets)은 object를 나타낸다. 예를 들면, binary 이미지에서 모든 white pixel의 집합으로 해당 이미지의 완전한 형태학적 설명이 된다.
binary 이미지에서, B의 reflection은 라 하고, 다음과 같이 정의된다.
B가 이미지에서 객체에 해당되는 2D points 픽셀 집합이라면, 는 단순히 B의 좌표들을 로 대체한 것이다.
B의 point 에 의한 translation은 라 하고, 다음과 같이 정의된다.
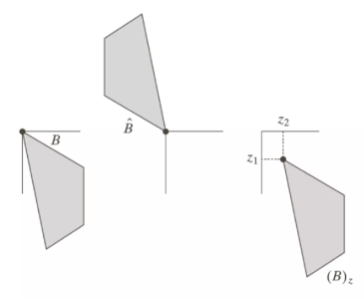
Set reflection과 translation은 형태학에서 structuring elements(SE)에 기반한 연산을 수행하기 위해 사용된다. structuring elements(구조 요소)란 이미지 상의 각 픽셀에 대해 중첩하여 비교하면서 형태학적 연산을 수행하는 기준이 되는 패턴 또는 모양이다.
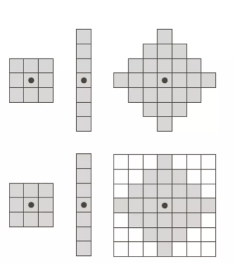
위 그림과 같이 구조 요소는 일반적으로 정사각형(가장 다수), 직사각형, 원형 구조가 사용될 수 있다.
형태학적 연산은 다양한 요소가 있지만, 여기서는 가장 basic한 연산만을 다룬다. 이는 일반적으로 Dilation(팽창), Erosion(침식), Opening(개방), Closing(폐쇄)에 해당한다.
Dilation and Erosion
* Dilation
A와 B가 2차원 픽셀 공간 의 집합일 때, B에 의한 A의 팽창은 A⊕ B로 표기되며, 다음과 같이 정의된다.
이 수식에서 는 B를 원점에 대해 반사(reflection)하고, 반사된 것을 z만큼 이동시킨 것이다. 여기서 B는 SE(구조 요소)로 가정한다. B에 의한 A의 팽창은 B와 A가 적어도 하나의 요소에서 겹치는 모든 이동 z의 집합니다. 이를 바탕으로 다음과 같이 팽창을 표현할 수 있다.
팽창은 이진 이미지에서 객체를 크게, 혹은 두껍게 만드는 연산이다. 객체가 두꺼워지는 정도는 사용하는 구조 요소의 모양에 따라 달라진다.
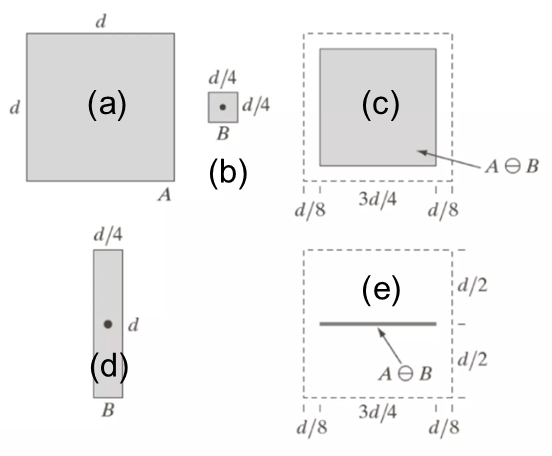
위 그림을 참조하면, 그림 (a)는 집합 A, (b)는 정사각형 모양의 구조 요소 B이다. 그림 (c)는 팽창의 결과이다. 그림 (d)는 수직 모양의 구조 요소로, (e)는 (d)의 구조 요소로 팽창된 결과이다.
팽창을 간단히 응용하자면, 빈 공간을 채우기 위해 사용할 수 있다.
아래 그림의 왼쪽을 보면, 끊어진 문자가 있다. 이 때 팽창을 사용하여 오른쪽 그림과 같이 끊어진 문자를 연결시킬 수 있다.

형태학적 접근의 이점은, 이진 이미지를 직접 결과로 도출해낸다는 것이다. 반면 저주파 필터링(lowpass filtering)의 경우 이진 이미지를 그레이스케일 이미지로 전환하고, 다시 이를 이진 형태로 변환하기 위해 임계값 함수를 한번 더 사용해야 한다.
* Erosion
A와 B가 2차원 픽셀 공간 의 집합일 때, B에 의한 A의 침식은 로 나타내며 다음과 같이 정의한다.
이 연산은 B에 의한 A의 침식이 z로 이동(translation)된 B가 A에 포함되는 모든 z의 집합임을 나타낸다. 여기서 B는 SE(구조 요소)로 가정한다.
B가 A에 포함되어야 한다는 것은, B가 A외의 요소(배경, )와 공통 요소가 존재하지 않는다는 것을 의미한다. 따라서, 침식을 다음과 같이 표현할 수 있다.
다음 그림은 침식의 한 예시이다.
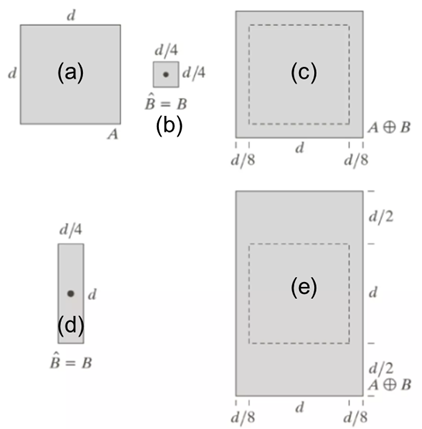
그림 (a)는 집합 A, (b)는 정사각형 모양의 구조 요소 B이다.
A, B 요소는 그림에서 음영 처리 된 부분이고, 나머지 배경 부분은 하얗다. 그림 (c)의 줄어든 사각형은 A에 대한 B의 침식 결과이다. 구조 요소 B가 A내에 포함되지 않게 되는 지점이 침식의 경계를 생성한다.
그림 (d)는 긴 직사각형 형태의 구조 요소이고, (e)는 (d) 형태의 구조 요소로 침식된 결과(직선 형태)이다.
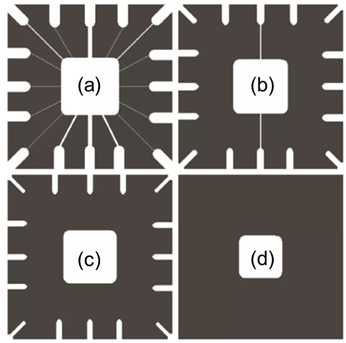
위 그림에서 그림(a)의 중앙 연결선을 제거하고 싶다고 하자. 그림 (b)는 11x11 크기의 정사각형 구조 요소를 사용하여 이미지를 침식시킨 것인데, 대부분의 선이 제거되었지만 두 개의 수직선은 제거되지 않고 가늘어졌다. 이 두 개의 수직선은 11픽셀보다 크기 때문에 완전히 제거되지 않은 것이다. 구조 요소 크기를 15x15로 변경하면 (c)와 같이 연결된 모든 선이 제거된다. 구조 요소를 45x45로 변경하면, 테두리에 있던 모든 선이 제거된다.
결국, 우리는 이 예제를 통해 침식이 이진 이미지의 객체를 수축시키거나, 가늘게 만든다는 것을 알 수 있다.
* Duality
침식과 팽창은 (여집합과 반사의 관점에서) 쌍대적인(dual) 연산이다.
위 식은 에 의한 의 침식의 여집합은 에 대한 의 팽창과 동일하며, 그 역도 성립함을 나타낸다. 쌍대성은 구조 요소가 원점에 대해 대칭적일 때 유용하므로, 이다.
유효성 증명
앞서 침식의 정의를 활용하면, 다음과 같이 표현할 수 있다.
가 A에 포함되면, 이고, 이전 표현식은 다음과 같게 된다.
를 만족하는 z 집합의 여집합은 를 만족하는 z 집합이다.
따라서,
Opening and Closing
* Opening
Opening(개방)은 객체의 윤곽을 부드럽게 하고, 좁은 틈을 끊거나 얇은 돌출부를 제거한다.
B에 의한 A의 개방은 로 표기되며 다음과 같이 정의된다.
즉, B에 의한 A의 침식 후 그 결과를 B로 팽창시키는 것과 같다. (Erosion→Dilation)
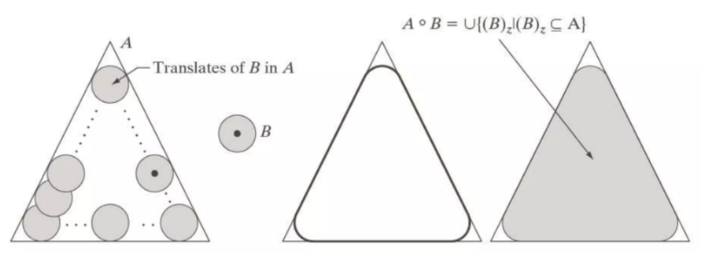
개방 연산은 간단한 기하학으로 해석될 수 있다. 위 그림에서와 같이 구조 요소 B를 “구르는 원형”으로 보면, 의 경계는 A 내부를 구르는 B로 도달한 가장 먼 지점에 의해 설정된다. 이는 B에 의한 A의 개방은 B의 모든 이동[]의 합집합()을 취하여 얻는다는 이론적 정의에 따른다. 즉, 개방은 다음과 같이 표현할 수 있다.
* Closing
Closing(폐쇄)는 개방과 마찬가지로 객체 윤곽을 부드럽게 하지만, 개방과는 달리 좁은 틈을 융합시키고 긴 굴곡을 없애며, 작은 구멍을 없애고 윤곽의 빈 부분을 채운다.
B에 의한 A의 폐쇄는 로 표기되며 다음과 같이 정의된다.
즉, B에 의한 A의 팽창 후 그 결과를 B로 침식시키는 것과 같다. (Dilation→Erosion)
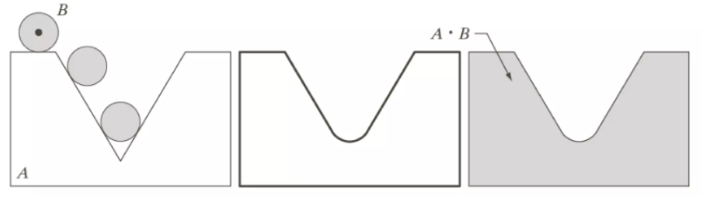
폐쇄 연산 또한 개방과 유사하게 기하학적으로 해석될 수 있다. 대신, 폐쇄에서는 B가 A의 외부를 구르게 된다. 즉, 개방에서는 내부의 가장자리를 처리하고, 폐쇄에서는 외부의 가장자리를 처리한다.
아래 그림은 개방과 폐쇄 연산을 보여준다.

* Properties of Opening/Closing
팽창, 침식과 같이, 개방과 폐쇄는 서로 쌍대적인 연산이다.
개방 연산은 다음 특성을 만족한다.
- 는 A의 부분집합(subimage)
- (*
idepotent property, 특정 연산이 반복 적용될 때 원래 값이 변하지 않는 성질을 가짐)- if ,
마찬가지로, 폐쇄 연산은 다음 특성을 만족한다.
- 는 A의 부분집합(subimage)
- if ,
