Linear Regression

최지안·2023년 10월 6일
Data Sciencemachine learningpython
0

Machine Learning

목록 보기
1/1

Definition

y^=θ0 +θ1x1 +θ2x2+ ... +θnxn\hat{y} = \theta_0\,+\theta_1x_1\,+\theta_2x_2 +\,...\,+ \theta_nx_n
  • y^\hat{y} : 예측값
  • n : feature의 개수
  • xix_i : i번째 feature value
  • θj\theta_j : i번째 모델 parameter (θ0:bias  term)(\theta_0 : bias\;term)
  • bias로 인해, x와 θ\theta는 n+1 차원
y^=θTx\hat{y} = \bold{\theta^Tx}

Cost Function

Error

error(i)=(y(i)−y^(i))2≥0error^{(i)} = (y^{(i)}-\hat{y}^{(i)})^2 \geq 0
💡 linear regression의 학습 목적: error를 최소화하는 parameter 최적화

SSE(X,θ\theta)

  • Sum of Squared Error
∑i=1m  (y(i)−θTx(i))2\sum_{i=1}^m\;(y^{(i)}-\theta^Tx^{(i)})^2

MSE(X,θ)\theta)

  • Mean of Squared error
1m∑i=1m  (y(i)−θTx(i))2\frac{1}{m}\sum_{i=1}^m\;(y^{(i)}-\theta^Tx^{(i)})^2

RMSE(X,θ)\theta)

  • Root Mean squared error
1m∑i=1m  (y(i)−θTx(i))2\sqrt{\frac{1}{m}\sum_{i=1}^m\;(y^{(i)}-\theta^Tx^{(i)})^2}

Design Matrix

사용 목적

  • model에 주어지는 training dataset

    (x(1),y(1)),(x(2),y(2)),(x(3),y(3)),  ⋯  (x(m),y(m))(x^{(1)}, y^{(1)}),\quad (x^{(2)}, y^{(2)}),\quad (x^{(3)}, y^{(3)}),\; \cdots \; (x^{(m)}, y^{(m)})

  • SSE

    (y(1)−θTx(1))2  +(y(2)−θTx(2))2  +(y(3)−θTx(3))2  +⋯  +(y(m)−θTx(m))2(y^{(1)}-\theta^Tx^{(1)})^2 \; + (y^{(2)}-\theta^Tx^{(2)})^2 \; + (y^{(3)}-\theta^Tx^{(3)})^2 \; + \cdots \;+ (y^{(m)}-\theta^Tx^{(m)})^2

  • 각 sample에 대한 예측값 → scalar

  • 위와 같은 수식을 단순화하기 위한 matrix

정의

  • M개의 sample들을 각각 row vector로 입력 → M x N matrix
X=∣x(1)Tx(2)Tx(3)T⋮x(m)T∣\bold{X} = \begin{vmatrix}x^{(1)T}\\x^{(2)T}\\x^{(3)T}\\\vdots\\x^{(m)T}\end{vmatrix}
  • X\bold X = M x N → vector 형식의 input을 쌓아서 matrix로 변환
  • θ\bold \theta = N x 1 → 기존의 scalar 형식이었던 예측값이 vector로 반환
y^=[y^(1)y^(2)y^(3)⋮y^(m)]=Xθ\bold{\hat{y}} = \begin{bmatrix}\hat{y}^{(1)} \\\hat{y}^{(2)} \\\hat{y}^{(3)}\\ \vdots \\\hat{y}^{(m)} \end{bmatrix} = \bold{X}\theta
SSE(θ)=∥y−y^∥22=∥y−Xθ∥22SSE(\theta) = \begin{Vmatrix}\bold{y-\hat y}\end{Vmatrix}^2_2 = \begin{Vmatrix}\bold{y-X\theta}\end{Vmatrix}^2_2

Normal Equation

정의

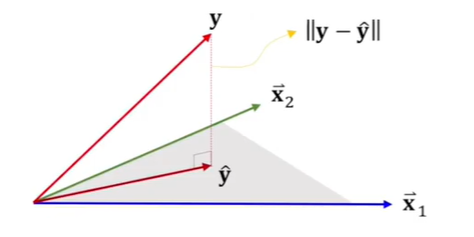
  • y^\hat y 는 x1,x2  …,  xnx_1, x_2\; \dots, \;x_n 이 생성하는 hyperplane → span {1,x1,x2…  xn}\{1, x_1, x_2 \dots\; x_n\} 상에 존재

  • Reisudal 또는 error의 크기 ∣∣y−y^∣∣||y-\hat y||를 최소화 하려면

    → 위의 hyperplane과 error y−y^y-\hat y가 서로 수직해야 함

    💡 즉, 모든 column vector에 대해서 xjT(y−y^)=0x^T_j(y-\hat y)=0 이 성립해야 함

→ 전체 m개의 sample에 대하여

XT(y−Xθ)=0⇒XTXθ=XTy\bold X^T(y-\bold {X\theta}) = 0 \Rightarrow \bold {X^TX\theta} = \bold X^Ty

💡 위 과정을 통해서 계산된 parameter θ^\hat \theta는 SSE(θ)SSE(\theta)를 minimize하는 해


θ^=(XTX)−1XTy\bold{\hat \theta = (X^TX)^{-1}X^Ty}

Gradient

정의

  • gradient → 기울기가 가장 증가하는 방향
  • 주어진 함수가 vector에서 scalar로 가는 함수가 있어야 함
f:Rn→Rf: \bold {\R^n} \rightarrow \bold {\R}
▽f:Rn→Rn\bigtriangledown f: \bold {\R^n} \rightarrow \bold {\R^n}
  • ex) 2차원 입력을 갖고, 자기자신에 대한 inner product로 정의된f(x1,x2)=x12  +  x22f(x_1,x_2) = x_1^2 \; +\; x_2^2 ▽f(x1,x2)=[∂f(X)∂x1∂f(X)∂x2]=[2x12x2]\bigtriangledown f(x_1,x_2) = \begin{bmatrix}\frac{\partial f(\bold X) }{\partial \bold x_1}\\\\\frac{\partial f(\bold X)}{\partial \bold x_2}\end{bmatrix} = \begin{bmatrix} 2x_1 \\\\ 2x_2 \end{bmatrix}

    • 첫번째 입력으로 미분한 값과 두번째 입력으로 미분한 값을 합쳐서 하나의 벡터를 구성

    • gradient는 gradient vector가 됨

    • gradient의 결과는 반드시 vector여야 함

      → gradient의 dimension은 입력이 2개이기 때문에 미분을 2번하고, 이를 vector로 만들면 dimension이 동일한 vector가 다시 나옴


Gradient Descent

정의

  • f(X)f(\bold X)가 min이 되는 X를 찾는 과정 [근사적][iterative]

  • ex)

    f(X)=XXTf(\bold X) = \bold {XX^T}, ▽f(X)=2X\bigtriangledown f(\bold X)=2\bold X, X1=[33]\bold X_1 = \begin{bmatrix} 3\\3\end{bmatrix}, ▽f(X1)=[66]\bigtriangledown f(\bold X_1) = \begin{bmatrix}6\\6\end{bmatrix}, η=0.1\eta = 0.1 (learning rate)


    X2=X1−0.1▽f(X1)=[2.42.4]\bold X_2 = \bold X_1 - 0.1\bigtriangledown f(\bold X_1) = \begin{bmatrix} 2.4 \\ 2.4 \end{bmatrix}

    X3=X2−0.1▽f(X2)=[1.921.92]\bold X_3 = \bold X_2 - 0.1\bigtriangledown f(\bold X_2) = \begin{bmatrix} 1.92 \\ 1.92 \end{bmatrix}


조건

  • f(x)가 미분 가능해야 함
  • global minimum을 보장 x → local minimum에 빠질 수 있음

Batch Gradient Descent

Linear Regression (y^=Xθ\hat y = \bold{X\theta})에 적용

J(θ)=SSE(θ)=∣∣y−Xθ∣∣2J(\bold \theta) = SSE(\bold \theta) = ||y-\bold {X\theta||^2} ⇒ batch learning에 해당

▽θJ(θ)=∂∂θJ(θ)=(y−Xθ)T(Y−Xθ)=yTy−2θTXTy+θTXTXθ=−2XTy+2XTXθ=2XT(Xθ−y)\bigtriangledown_\theta J(\bold \theta) = \frac{\partial}{\partial \bold \theta}J(\bold \theta)\\ \qquad=\bold {(y-X\theta)^T (Y-X\theta)}\\ \qquad=\bold{y^Ty - 2\theta^TX^Ty + \theta^TX^TX\theta}\\ \qquad= -2\bold{X^Ty + 2X^TX\theta}\\ \qquad= 2X^T\bold{(X\theta-y)}


💡 ▽θJ(θ)=2XT(Xθ−y)\bigtriangledown_\theta J(\bold \theta) = 2X^T\bold{(X\theta-y)}

Batch and oneline learning

배치 러닝 batch learning

  • 가용한 데이터를 한번에 모두 사용해서 학습
  • 시간 및 컴퓨팅 자원 많이 사용
  • 새로운 데이터 셋이 주어지면, 처음부터 다시 학습
  • 부드럽게 해에 접근하지만, 지역 최적값(local optima)에 빠져 못 나올 수 있음

미니 배치 러닝 mini-batches learning

  • 데이터 셋을 미니 배치라고 하는 작은 그룹으로 나누어 학습
  • 배치 방식과 온라인 방식의 절충
  • 기울기 (gradient)가 온라인 학습보다 정확, 지역 최적값 문제에서 배치 학습보다 우수
  • 대부분 프로그램에서 미니 배치 방식 사용

온라인 러닝 oneline learning

  • 데이터를 순차적으로 처리하면서 점증적으로 학습
  • 각 학습 단계가 빠름
  • 배치 러닝보다 불규칙하게 접근하지만 지역 최적값 문제에서 유리
  • 데이터가 순차적으로 들어오는 경우에 적합
  • 컴퓨팅 자원이 매우 제한적일 때 적합

Stochastic gradient descent

  • 무작위로 선택한 한 개의 sample에 대해서만 gradient를 계산하여 parameter를 update
  • sequential learning or oneline learning
  • 대규모 데이터 셋 처리에 유리
  • 선택하는 사례의 무작위성으로, 움직임이 불규칙
  • BGD에 비해 local optimum에서 쉽게 빠져나옴
  • 최적해에 도달하지만, 지속적으로 요동
  • BGD와 마찬가지로 global optimum이라는 보장 x

Learning Rate

Learning rate

  • Hyperparameter인 학습률 (learning rate)이 너무 작은 경우 → 시간이 오래 걸림
  • 너무 큰 경우, 최적해를 지나쳐 해를 못 찾을 수 있음 → local optima 탈출 가능

∴ Constant Learning rate : 보통 0.1, 0.01부터 시작하여 어러 값으로 시험해가며 범위를 좁힘

Time-based decay

η=η01+kt\eta = \frac{\eta_0}{1+kt}
  • η0\eta_0: 학습률 초기값, k: parameter, t: iteration

Step decay

  • 정해진 epoch마다 학습률을 줄이는 방법
  • ex) 5 epoch마다 절반, 20 epoch마다 1/10
  • epoch: 훈련 데이터셋 전체를 모두 사용하는 경우

Exponential decay

η=η0e−kt\eta = \eta_0e^{-kt}
  • η0\eta_0: 학습률 초기값, k: parameter, t: iteration

Summary

Normal Equation

θ^=(XTX)−1XTy\bold{\hat \theta = (X^TX)^{-1}X^Ty}

→ 이때 구해지는 θ^\hat \theta는 J(θ)J(\bold \theta)의 argmin

Gradient Descent

Batch Learning

θn+1=θn−η{2XT(Xθ−y)}\bold{\theta_{n+1} = \theta_n-\eta\{2X^T(X\theta-y)\}}

Stochastic Learning

θn+1=θn−η{2X(t)T(θTX(t)−y(t))}\bold{\theta_{n+1} = \theta_n -\eta\{2X^{(t)T}(\theta^TX^{(t)}-y^{(t)})\}}

→ t는 특정 sample을 의미

profile
최지안

0개의 댓글