2021 KAKAO BLIND RECRUITMENT - 합승 택시 요금 (파이썬) 문제 및 풀이

문제

programmers.co.kr/learn/courses/30/lessons/72413
지점의 개수 n, 출발지점을 나타내는 s, A의 도착지점을 나타내는 a, B의 도착지점을 나타내는 b, 지점 사이의 예상 택시요금을 나타내는 fares가 매개변수로 주어집니다. 이때, A, B 두 사람이 s에서 출발해서 각각의 도착 지점까지 택시를 타고 간다고 가정할 때, 최저 예상 택시요금을 계산해서 return 하도록 solution 함수를 완성해 주세요.

풀이

전형적인 그래프에서의 최단 거리 문제다. 그래프에서 최단 거리를 구할 수 있는 알고리즘에는 대표적으로 다익스트라와 플로이드 와샬이 있다. 문제를 보면서 이 중에서 어떤 알고리즘으로 문제를 해결할 수 있을지 보자. 먼저 합승이 끝나는 지점을 T라고 하자. 그러면 우리가 최종적으로 구해야 하는 것은 { 비용(S - T) + 비용(T - A) + 비용(T - B) }의 최소이다. 즉, S에서 모든 지점까지의 최소 비용, A에서 모든 지점까지의 최소 비용, B에서 모든 지점까지의 최소 비용을 계산하여 모든 지점을 경유하여 최소를 구하면 된다. 또한 n의 개수가 200개로 적은 편이다. 이런 해법에 맞는 알고리즘은 플로이드 와샬 알고리즘이다.

1. 충분히 큰 값을 의미하는 10억을 INF로 설정하고 n x n 그래프를 정의한다.
2. 자기 자신에게 가는 비용은 0으로 설정한다.
3. 이동 방향에 따라 비용이 달라지지 않으므로 graph[출발][도착] = graph[도착][출발] = 비용
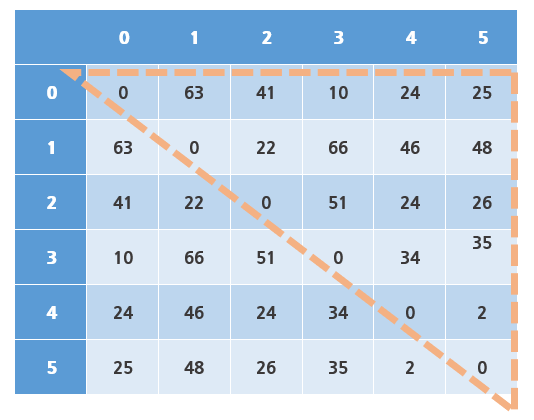
4.  모든 지점에 대하여 점 T에 대한 최소 비용을 구한다. 이때, 이동 방향에 따라 비용이 달라지지 않음에 따라 우리는 그래프의 모든 행과 열을 탐색할 필요가 없다. (아래 표 참고)
5. 점 T를 모든 지점을 돌면서 시작점 S, 두 도착 지점 A와 B에 대하여  { 비용(S - T) + 비용(T - A) + 비용(T - B) }의 최소를 구하면 된다.

표를 보면 자기 자신에게 가는 비용을 기준으로 위쪽 부분에 대해서만 최소 비용을 구하면 되는 것을 알 수 있다. 

코드

import sys
input = sys.stdin.readline

def solution(n, s, a, b, fares):
    INF = int(1e9)
    graph = [[INF] * n for _ in range(n)]
    for i in range(n):
        graph[i][i] = 0

    for i in fares:
        graph[i[0] - 1][i[1] - 1] = i[2]
        graph[i[1] - 1][i[0] - 1] = i[2]

    for t in range(n):
        for i in range(n):
            for j in range(i, n):
                if i != j:
                    temp = min(graph[i][j], graph[i][t] + graph[t][j])
                    graph[i][j] = graph[j][i] = temp


    answer = INF
    for t in range(n):
        temp = graph[s - 1][t] + graph[t][b - 1] + graph[t][a - 1]
        answer = min(answer, temp)

    return answer

회고

다른 분은 heapq 모듈의 우선순위 큐를 통해 다익스트라 알고리즘을 구현해 문제를 풀었다. 다익스트라 알고리즘을 이용해 충분히 문제를 풀 수 있다는 것을 알 수 있고, 이 방식(ElogV)이 내 풀이(V^3)보다 시간 복잡도가 효율적이다. 플로이드 워샬 알고리즘보다 구현이 어려운 편이니 언제든지 응용할 수 있도록 충분히 연습해 놓자.

import heapq

def solution(n, s, a, b, fares):

    link = [[] for _ in range(n+1)]
    for x, y, z in fares:
        link[x].append((z, y))
        link[y].append((z, x))

    def dijkstra(start):
        dist = [987654321] * (n + 1)
        dist[start] = 0
        heap = []
        heapq.heappush(heap, (0, start))
        while heap:
            value, destination = heapq.heappop(heap)
            if dist[destination] < value:
                continue

            for v, d in link[destination]:
                next_value = value + v
                if dist[d] > next_value:
                    dist[d] = next_value
                    heapq.heappush(heap, (next_value, d))
        return dist

    dp = [[]] + [dijkstra(i) for i in range(1, n+1)]
    # print(dp)
    answer = 987654321
    for i in range(1, n+1):
        answer = min(dp[i][a] + dp[i][b] + dp[i][s], answer)

    return answer