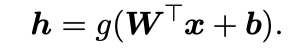Ch6. Deep Feedforward Networks

TIMESTAMP
@200927 시작

들어가기 전에

• 심층 순방향 네트워크, 순방향 심층망, 또는 다층 퍼셉트론은 딥러닝의 본질적인 딥러닝 모델로(Deep feedforward networks, feedforward neural networks, multilayer perceptron), 특정 함수 $f^*$에 근사하는 것이 목적이다.

  • 예를 들어 분류를 위해서 $y=f^*(\bm{x})$은 입력값 $\bm{x}$를 카테고리 $y$에 매핑시킨다.
  • 순방향 네트워크는 매핑 $\bm{y}=f(\bm{x};\bm{\theta})$을 정의하고, 가장 최적의 함수 근사를 나타내는 파라미터 $\bm{\theta}$값을 학습시킨다.

• 이러한 모델을 순방향(feedforward)라고 한다. 함수를 통해 $\bm{x}$로부터 $f$의 중간 계산을 거쳐 최종 결과 $\bm{y}$까지 정보가 흐르기 때문이다.

  • 이때 모델의 결과가 다시 돌아가는 피드백(feedback)은 없다.
  • 순방향 심층망이 피드백 연결을 포함하게 되면 이는 챕터 10에서 다루는 순환신경망(recurrent neural networks)가 된다.

• 순방향 네트워크는 머신러닝 실무자에게 매우 중요하며, 상업적 응용의 기초를 형성한다.

  • 예를 들어 사진에서의 물체인식에 사용되는 컨볼루션 네트워크는 순방향 네트워크의 한 종류이다.
  • 순방향 네트워크는 자연어 처리에 응용되는 많은 순환신경망의 개념적인 기반이 된다.

• 순방향 신경망은 일반적으로 많은 다양한 함수의 조합으로 나타나기 때문에 네트워크(network)라고 불린다. 함수가 서로 어떻게 구성되어 있는지 나타내는 directed acyclic graph와 관련이 있다.

  • 예를 들어 순차적으로 연결된 세 개의 함수 $f^{(1)},f^{(2)},f^{(3)}$를 통해 $f(\bm{x})=f^{(3)}(f^{(2)}(f^{(1)}(\bm{x})))$를 구성할 수 있다.
  • 이러한 체인 구조는 가장 일반적으로 사용되는 신경망 구조이다.
  • 이 경우 $f^{(1)}$은 네트워크의 첫번째 층(first layer)이고, $f^{(2)}$는 두번째 층(second layer)이다. 순방향 네트워크의 마지막 층을 결과층(output layer)이라고 한다.
  • 체인의 전체 길이는 모델의 깊이(depth)이고, 이로 부터 "딥러닝"이라는 용어가 탄생하게 된다.
  • $f^*(\bm{x})$를 매치하기 위해 신경망을 학습하며, 학습 데이터는 각기 다른 지점에서 평가된 noisy, approximate한 $f^*(\bm{x})$의 예들을 제시한다.
    • 각 샘플 $\bm{x}$은 레이블 $y\approx f^*(\bm{x})$을 동반하고 있다.
  • 학습 예제들은 각 점 $\bm{x}$에서의 결과층이 $y$에 가까운 값을 나타내야할 것을 직접적으로 명시하지만, 다른 층은 학습 데이터에 대해서 직접적으로 명시되지 않는다.
  • 학습 알고리즘은 반드시 어떻게 이러한 층을 사용해서 원하는 결과값을 생성하도록 할지 결정해야하지만, 학습 데이터는 각 층이 무엇을 해야하는지를 말하지 않는다. 대신, 학습 알고리즘은 $f^*$를 가장 잘 근사하기 위해 이러한 층들을 어떻게 사용할 지를 결정한다. 학습데이터가 이러한 각 층이 나타내야할 결과를 말하지 않기 때문에, 이러한 층들을 은닉층(hidden layers)라고 한다.

• 마지막으로, 이러한 네트워크는 신경과학으로부터 영감을 받았기 때문에 neural이라고 불리운다. 네트워크의 각 은닉층은 보통 벡터값이며, 은닉층의 차원은 모델의 width을 결정한다.

  • 벡터의 각 요소는 뉴런과 유사한 역할을 하는 것으로 해석될 수 있다. 층을 단순히 vector-to-vector 함수를 나타내는 것으로 생각하는 것 대신, 층이 병렬적으로 작동하는 많은 유닛(unit)으로 구성되는 것으로 생각할 수 있으며, 이때 각각은 vector-to-scalar 함수를 나타낸다. 각 유닛은 다른 많은 유닛에서 입력을 받고 자체 활성화 값을 계산한다는 점에서 뉴런과 유사하다.
  • 여러 vector-valued represention 층을 사용하는 아이디어는 신경과학에서 유래되었다. 이러한 representations를 계산하는 데 사용되는 함수 $f^{(i)}(\bm{x})$의 선택은 생물학적 뉴런이 계산하는 함수에 대한 신경과학적 관찰에 의해 아이디어를 얻는다.
  • 하지만 현대의 신경망 연구는 많은 수학적, 공학적 분야의 지도를 받고 있으며, 신경망의 목적은 뇌를 완벽하게 모델링하는 것이 아니다. 순방향 네트워크를 통계적 일반화를 달성하도록 설계된 함수 근사 기계로 생각하는 것이 가장 좋으며, 때로는 뇌 기능의 모델이 아니라 뇌에 대해 알고 있는 정보로부터 통찰력을 일부 이끌어낸다.

• 순방향 네트워크를 이해하는 한가지 방법은 선형모델로 시작하여 한계를 극복하는 방법을 생각하는 것이다.

  • 로지스틱 및 선형 회귀와 같은 선형모델은 closed form이나 컨벡스 최적화를 통해서 효율적이고 안정적으로 적합할 수 있기 때문에 매력적이다.
  • 선형모델에는 model capacity가 선형함수로 제한된다는 점에서 명백한 한계가 있으므로, 모델은 두 입력 변수 간의 상호작용을 이해할 수 없다.

• 선형모델을 $\bm{x}$에 대한 비선형 함수로 확장시키기 위해서 $\bm{x}$ 자체가 아니라 변환된 입력 $\phi(\bm{x})$에 선형모델을 적용할 수 있고, 이 때 $\phi$는 비선형 변환이다.

  • 이와 동일하게, 세션 5.7.2에 제시된 커널 트릭을 적용하여 암시적으로 $\phi$ 매핑에 기반한 비선형 학습 알고리즘을 얻을 수 있다.
  • $\phi$를 $\bm{x}$를 설명하는 a set of features으로 생각하거나, $\bm{x}$의 새로운 representation이라고 할 수 있다.

Q. 그렇다면 어떻게 매핑 $\phi$를 선택할 것인가?

1. 한가지 옵션은 매우 일반적인 $\phi$를 사용하는 것이다.
   • 예: RBF 커널에 기반한 커널기계에서 암시적으로 사용되는 무한 차원 $\phi$
   • 만약 $\phi({\bm{x}})$의 차원이 충분히 높으면 항상 학습셋을 맞추는 충분한 capacity를 가질 수 있지만 테스트셋에 대한 일반화는 좋지 않다.
   • 아주 일반적인 피쳐 매핑은 보통 local smoothness의 원칙에만 기반하며, 심화된 문제를 풀기 위한 사전 정보를 충분히 encode하지 않는다.
2. 또 다른 옵션은 수동적으로 $\phi$를 설정하는 것이다.
   • 딥러닝의 출현 이전에 지배적인 방법으로, 음성 인식 또는 컴퓨터 비전과 같이 다른 영역을 전문으로 하고 도메인 간 교류가 거의 없는 실무자들과 함께 각 개별 작업에 수십 년의 인간의 노력을 필요로 한다.
3. 딥러닝의 전략은 $\phi$를 배우는 것으로, $y=f(\bm{x};\bm{\theta},\bm{w})=\phi(\bm{x};\bm{\theta})^T\bm{w}$모델을 가진다.
   • 파라미터 $\bm{\theta}$는 광범위한 함수로부터 $\phi$를 학습하기 위해 사용되고, 파라미터 $\bm{w}$는 $\phi(\bm{x})$로부터 원하는 결과값을 매핑한다. 이는 은닉층을 정의하는 $\phi$을 포함하는 심층 순방향 네트워크의 예시이다.
   • 이 접근은 학습 문제의 convexity를 포기하는 세 가지 중 유일한 방법이지만 장점이 단점을 훨씬 능가한다. 이 접근에서는 representation을 $\phi( \bm{x}; \bm{\theta})$로 파라미터화하고 최적화 알고리즘을 사용하여 최적의 representation에 대응되는 $\bm{\theta}$를 찾는다.
   • $\phi( \bm{x}; \bm{\theta})$는 매우 포괄적이라서 첫 번째 접근 방식의 이점을 포착할 수 있다. 또한 두 번째 접근의 이점을 살릴 수 있다. 본인이 알고 있는 것을 인코딩하여 $\phi( \bm{x}; \bm{\theta})$를 디자인함으로써 일반화에 사용할 수 있다.
   • 인간이 올바른 함수를 정확하게 찾는 것보다 올바른 일반적인 함수 패밀리(general funcion family)를 찾기만 하면 된다는 것이 장점이다.

• 피쳐를 학습하여 모델을 개선하는 이 일반적인 원칙은 이 챕터에서 다루는 순방향 네트워크를 넘어서 확장된다. 딥러닝에서 반복되는 주제로 이 책 전반을 걸쳐 설명되는 모든 종류의 모델에 적용된다.

  • 순방향 네트워크는 피드백 연결 없이 $x$에서 $y$의 결정론적인(deterministic) 매핑을 학습하는 데 이 원칙을 적용한 것이다.
  • 나중에 나오는 다른 모델들은 이 원칙을 확률적인(stochastic) 매핑이나 피드백이 있는 함수, 그리고 단일 벡터에 대한 확률 분포를 학습하는 데 적용할 것이다.

• 순방향 네트워크의 간단한 예제로 이 챕터를 시작한다. 그 다음, 순방향 네트워크를 배포하는 데 필요한 각 설계 디자인을 다룬다.

  • 첫째로, 순방향 네트워크를 학습하는 것에는 선형모형에 필요한 것과 동일한 결정을 많이 해야 하며, 옵티마이저, 비용함수, 결과 유닛의 형태가 있다.
  • 이러한 gradient 기반의 학습의 기본 사항을 리뷰하고, 다음 순방향 네트워크에 한정된 몇 가지 결정사항을 확인한다.
  • 순방향 네트워크는 은닉층의 개념을 도입했고, 이로 인해 활성함수(activation functions)를 선택하여 은닉층의 값들을 계산해야 한다.
  • 또한 네트워크 구조를 설계해야 한다(네트워크에 레이어 수를 몇 개를 가질지, 이러한 레이어가 서로 어떻게 연결될 것인지, 각 층에 몇 개의 유닛을 가질지).
  • 심층 신경망에서의 학습은 복잡한 함수의 기울기를 계산하는 것을 필요로 한다. 이러한 기울기를 효율적으로 계산하는 Back-propagation 알고리즘과 현대적인 일반화를 다루며, 몇 가지 역사적인 관점에서 이 장을 마친다.

Example: Learning XOR

• 순방향 네트워크의 아이디어를 견고히 하기 위해서, 매우 간단한 XOR 함수를 학습하는 예제를 살펴본다.

• XOR 함수는 두 개의 이진값($x_1, x_2$)에 대한 계산으로, 둘 중 하나만이 1일 때 XOR은 1을 반환하고 그 외에는 0이다. XOR 함수는 우리가 학습하고자 하는 타겟 함수 $y=f^*(\bm{x})$를 가진다. 우리의 모델은 $y=f(\bm{x};\bm{\theta})$ 함수를 가지고 학습 알고리즘은 파라미터 $\bm{\theta}$를 조정하여 최대한 $f$를 $f^*$에 유사하도록 만들 것이다.

• 이 간단한 예제에서 우리는 통계적인 일반화에는 관심이 없고 이 네트워크가 4개의 점 $\mathbb{X}=\{[0,0]^\top,[0,1]^\top,[1,0]^\top,[1,1]^\top \}$ 에 올바르게 작동하기를 원한다. 이 4개의 점에 네트워크를 학습할 것이고 학습 셋에 적합 시키고자 한다.

• 이 문제를 회귀 문제로 다룰 수 있고 손실 함수로 mean squared error를 사용할 수 있다. 이 예제의 수학을 가장 단순화 시키기 위해 이 손실함수를 선택한다.

  • 실제로는, MSE가 이진 데이터를 모델링 하는데 적합한 비용함수가 아니며, 더 적합한 접근은 섹션 6.2.2.2에 제시되어 있다.

• 전체 학습셋에 대해서 MSE 손실함수 다음과 같다.

  $J(\bm{\theta})=\frac{1}{4}\sum_{x\in \mathbb{X}}(f^*(\bm{x})-f(\bm{x};\bm{\theta}))^2$

• 모델의 형태 $f(\bm{x};\bm{\theta})$를 선택해야 한다. $\bm{w}$와 $b$로 구성된 $\bm{\theta}$의 선형모형을 선택했다고 가정한다면 모델은 다음과 같다.

  $f(\bm{x};\bm{w},b)=\bm{x}^\top \bm{w}+b$

  정규방정식(normal equation)을 통해 닫힌 형태로 $\bm{w}$와 $b$에 대해 $J(\bm{\theta})$를 최소화할 수 있다.
  

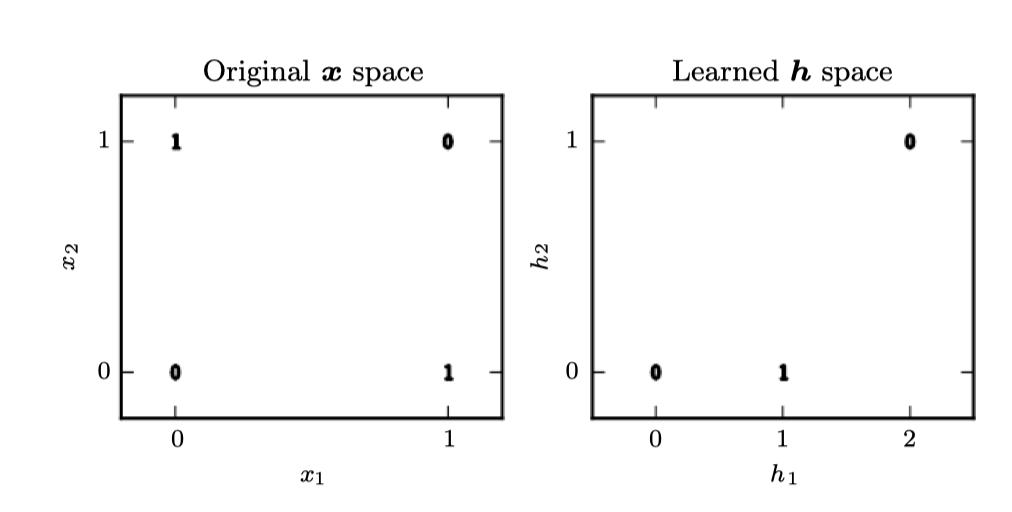
• 정규방정식을 풀면 $\bm{w=0}$과 $b=\frac{1}{2}$가 나오며 선형모형은 단순히 모든 곳에 $0.5$가 나온다. 왜 이런 일이 나오는가? 위의 그림은 왜 선형모형이 XOR 함수를 나타낼 수 없는지를 나타낸다. 이를 해결할 수 있는 한 방법은 다른 피쳐 공간을 학습하는 모형을 사용하여 선형모형으로 나타낼 수 있도록 하는 것이다.
  

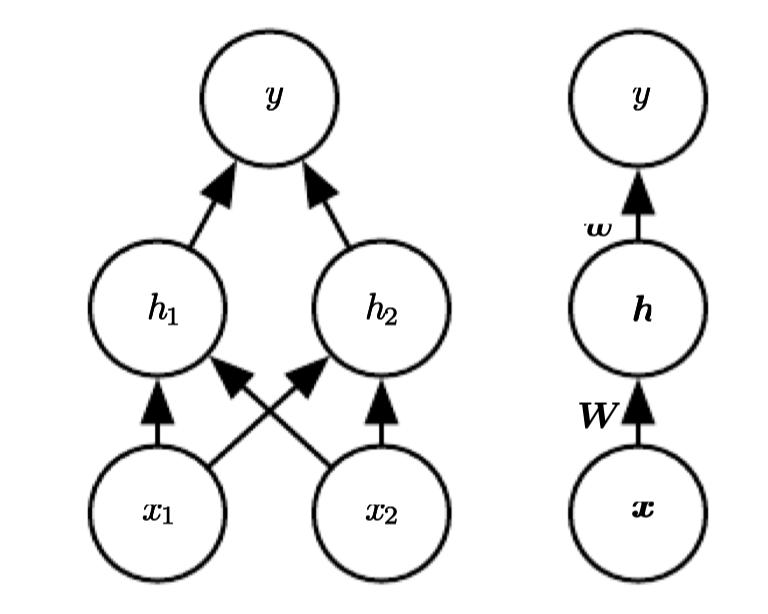
• 여기서 두 개의 은닉유닛을 가지는 은닉층 한개의 순방향 네트워크를 사용할 것이다. 이 순방향 네트워크는 은닉유닛 $\bm{h}$의 벡터를 가지며, 이는 $f^{(1)}(\bm{x};\bm{W},\bm{c})$에 의해 계산된다. 은닉유닛의 값들은 다음 두번째 층의 입력으로 사용된다. 두번째 층은 네트워크의 결과층이다. 결과층은 여전히 선형회귀모형이지만 $\bm{x}$가 아닌 $\bm{h}$에 대한 것이다. 이 네트워크는 이제 두 개의 함수가 서로 체인된 형태로, $\bm{h}=f^{(1)}(\bm{x};\bm{W},\bm{c})$, $y=f^{(2)}(\bm{h};\bm{w},b)$이며 전체 모델은 $f(\bm{x};\bm{W},\bm{c},\bm{w},b )=f^{(2)}(f^{(1)}(\bm{x}))$이다.

• 함수 $f^{(1)}$는 무엇을 계산해야 하는가? 선형모형은 지금까지 잘 작동했기에 $f^{(1)}$ 또한 선형으로 할 수 있지만, 만약 그렇게 되면 전체 순방향 네트워크는 입력값의 선형 함수로 남게 될 것이다. 여기서 절편은 일단 무시하고 $f^{(1)}(\bm{x})=\bm{W}^\top \bm{x}$이고 $f^{(2)}(\bm{h})=\bm{h}^\top \bm{x}$라고 하면, 결국 $f(\bm{x})=\bm{w}^\top \bm{W}^\top \bm{x}$이 되고 $\bm{w'}=\bm{W}\bm{w}$인 $f(\bm{x})=\bm{x}^\top\bm{w}'$가 된다.

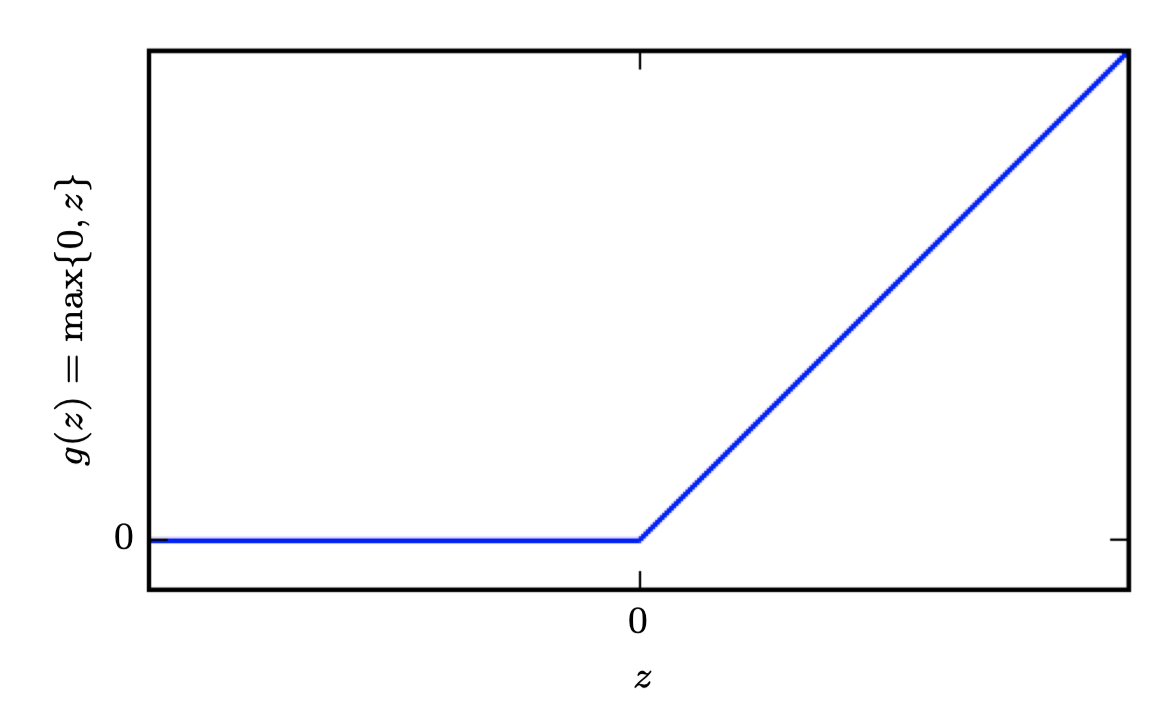
• 그러므로 피쳐를 설명하기 위해서는 비선형 함수를 반드시 써야 한다. 대부분의 신경망은 affine 변환을 사용하며, 이는 학습된 파라미터와 활성함수라고 불리는 고정된 비선형 함수에 의해 작동된다. 이 전략을 사용하여 $\bm{h}=g(\bm{W}^\top\bm{x}+\bm{c})$로 정의하며, 이 때 $\bm{W}$는 선형변환의 가중치이고 $\bm{c}$는 바이어스이다. 이전에 선형회귀모형에서 가중치 벡터와 바이어스 스칼라 파라미터를 사용하여 입력값 벡터에서 결과값 스칼라로 affine 변환을 나타냈다. 지금은 벡터 $\bm{x}$로 부터 $\bm{h}$로 affine 변환하며, 바이어스 벡터 파라미터가 필요하다. 활성함수 $g$는 보통 요소별(element-wise)로 적용되는 $h_i=g(\bm{x}^\top\bm{W}_{:,i}+c_i)$ 함수가 선택된다. 현대의 신경망에서는 ReLU (recified linear unit)을 사용하는 것이 기본적으로 추천되며, $g(z)=\max\{0,z\}$이다.
  

• 전체 네트워크는 다음과 같이 쓸 수 있다.

  $f(\bm{x};\bm{W},\bm{c},\bm{w},b)=\bm{w}^\top \max{0,\bm{W}^\top\bm{x}+\bm{c}}+b$

• XOR 문제의 솔루션은 다음과 같다.

  $\bm{W}=\begin{bmatrix} 1&1\\1&1\end{bmatrix}, \bm{c}=\begin{bmatrix} 0\\-1\end{bmatrix},\bm{w}=\begin{bmatrix} 1\\-2\end{bmatrix}, b=0 \\ \quad \\ \bm{X}=\begin{bmatrix} 0&0\\0&1\\1&0\\1&1\end{bmatrix}, \bm{XW}=\begin{bmatrix} 0&0\\1&1\\1&1\\2&2\end{bmatrix}, \bm{XW+c}=\begin{bmatrix} 0&-1\\1&0\\1&0\\2&1\end{bmatrix}$

• 이 공간에서 모든 예제는 기울기 1인 선을 따라 존재한다. 이 선을 따라 움직이면 결과는 $0$에서 시작하여 $1$이 되었다가 다시 $0$이 되어야 한다. 선형모형은 이러한 함수를 표현할 수 없다. 각 샘플에서 $\bm{h}$값을 계산하기 위해서 recified 선형변환을 적용한다:

  $\\\bm{h}=\begin{bmatrix} 0&0\\1&0\\1&0\\2&1\end{bmatrix}$

  이 변환은 샘플 간의 관계를 변화시켰다. 더 이상 단일 직선에 따라 존재하지 않으며 선형모형이 이 문제를 풀 수 있도록 하는 공간에 존재한다.

• 마지막으로 가중치 벡터 $\bm{w}$를 곱하면, 이 신경망은 모든 예제에 알맞는 답을 가지게 된다.

  $\\\text{output}=\begin{bmatrix} 0\\1\\1\\2\end{bmatrix}$

• 이 예에서는 단순히 솔루션을 지정한 다음 오류가 0임을 보였다. 실제 상황에서는 수십억 개의 모델 파라미터와 수십억 개의 학습 샘플이 있을 수 있으므로 여기에서 한 것처럼 단순히 솔루션을 추측 할 수 없다.

• 대신 gradient 기반 최적화 알고리즘은 오류가 거의 발생하지 않는 파라미터를 찾을 수 있다. XOR 문제에 대해 설명한 솔루션은 손실 함수의 global minimum이므로 경사 하강법이 이 지점으로 수렴 할 수 있다. 경사 하강법도 찾을 수있는 XOR 문제에 대한 다른 동등한 솔루션이 있다. 경사 하강법이 수렴하는 점은 파라미터의 초기 값에 따라 다르다. 실제로 경사 하강법은 일반적으로 여기에서 제시 한 것과 같은 깨끗하고 이해하기 쉬운 정수 값 솔루션을 찾지 못한다.

Gradient-Based Learning

• 신경망을 설계하고 학습하는 것은 경사하강법으로 다른 머신러닝 모델을 학습하는 것과 크게 다르지 않다. 섹션 5.10에서 최적화 과정, 비용함수, 모델을 지정하여 머신러닝 알고리즘을 구축하는 방법을 설명했다.

• 지금까지 살펴본 선형모형과 신경망 간의 가장 큰 차이점은 신경망의 비선형성으로 인하여 손실함수가 non-convex하게 된다는 것이다. 즉, 신경망은 일반적으로 반복적인 gradient 기반 최적화 옵티마이저를 사용하여 학습하는 것으로 비용함수를 매우 낮은 값으로 유도한다.

  • 이는 선형회귀모형이나 로지스틱회귀 혹은 SVM을 학습하기 위해 사용되는 global convergence가 보장된 컨벡스 최적화 알고리즘을 위해 선형방정식을 푸는 것과는 다르다. 컨벡스 최적화는 어떤 초기 파라미터에서 시작하더라도 수렴한다(이론상은 그렇지만 실제로는 많은 수치적인 문제가 발생할 수 있다).
  • non-convex 손실함수에 적용되는 확률적 경사하강법은 이러한 수렴에 대한 보장이 없으며, 초기 파라미터 값들에 민감하다. 순방향 네트워크의 경우 모든 가중치를 작은 임의의 값으로 초기화하는 것이 중요하다. 바이어스는 0이나 작은 양수로 초기화될 수 있다.
  • 순방향 네트워크와 거의 모든 심층 모델을 학습하기 위해 사용되는 반복적인 gradient 기반 최적화 알고리즘은 8장에서 자세히 다뤄질 예정이며, 특히 섹션 8.4에서는 파라미터 초기화를 설명한다. 지금은 학습 알고리즘이 거의 항상 gradient를 사용하여 비용함수를 어떻게든 하강하도록 한다는 사실을 이해하면 된다. 특정 알고리즘은 섹션 4.3에 소개된 경사하강법의 아이디어에 대한 개선 및 수정이며, 보다 구체적으로 섹션 5.9에 소개된 확률적 경사하강법 알고리즘의 개선이다.

• 물론 선형회귀와 경사하강법을 사용하는 SVM와 같은 모델도 학습할 수 있고, 실제로는 학습셋이 굉장히 클 때 일반적인 방법이다. 이러한 관점에서 신경망 학습은 다른 모델 학습과 크게 다르지 않다. Gradient 계산은 신경망에서 조금 더 복잡하지만 여전히 효율적이고 정확하게 수행할 수 있다. 섹션 6.5에서는 역전파와 현대적인 일반화 버전을 사용하여 gradient을 구하는 방법을 설명한다.

  다른 머신러닝 모델과 마찬가지로 gradient 기반 학습을 적용하기 위해서는 (1) 비용함수를 선택하고 (2) 모델의 결과값을 어떻게 나타낼 것인지를 선택해야 한다.

Cost Functions

• 심층 신경망 설계의 중요한 측면은 비용함수를 선택하는 것이며, 다행히 신경망의 비용함수는 선형모형과 같이 다른 parametric 모델과 거의 비슷하다.

많은 경우에 parametric model은 분포 $p(\bm{y}|\bm{x};\bm{\theta})$를 정의하고 maximum likelihood의 원칙을 사용한다. 이는 학습데이터와 모델의 예측 사이의 cross-entropy를 비용함수로 쓴다는 의미이다.

• 가끔은 좀 더 간단한 방법으로 $\bm{y}$에 대해 완전한 확률분포를 예측하는 것이 아니라 단지 $\bm{x}$에 대한 $\bm{y}$를 예측한다. 이러한 측정치의 예측기를 학습할 수 있는 손실함수를 사용한다.

신경망을 학습하는 데 사용하는 총 비용함수는 여기서 다루는 비용함수 하나와 정규화를 합친다.

• 섹션 5.2.2에 이미 선형모형에서 정규화의 간단한 예제 몇 개를 다루었다. 선형모형에서 사용되는 weight decay는 심층 신경망에 바로 적용할 수 있으며 가장 유명한 정규화 방법 중 하나이다. 신경망에서 더욱 심화된 정규화 전략은 7장에서 다뤄질 것이다.

Learning Conditional Distributions with Maximum Likelihood

• 대부분의 최신 신경망은 maximum likelihood를 사용하여 훈련된다. 이는 비용함수가 단순히 negative log-likelihood라는 것을 의미하며, 학습 데이터와 모델 분포 간의 cross-entropy와 동일하다. 비용함수는 다음과 같다.
  $J(\bm{\theta})=-\mathbb{E}_{\mathbf{x,y} \sim \hat{p}_{\text{data}}} \log p_{\text{model}}(\bm{y}|\bm{x})$

Learning Conditional Statistics

functional
calculus of variations
mean absolute error

[FIRST RESULT] Mean squared error (mean of y for each value of x)

• In other words, if we could train on infinitely many samples from the true data generating distribution, minimizing the mean squared error cost function gives a function that predicts the mean of y for each value of x .

[SECOND RESULT] Mean absolute error (median of y for each value of x)

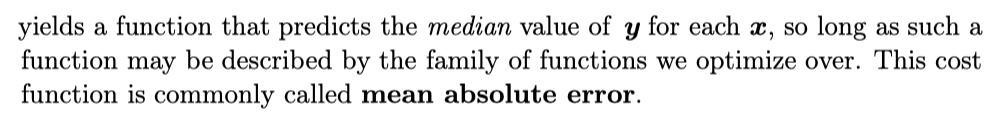
Unfortunately, mean squared error and mean absolute error often lead to poor results when used with gradient-based optimization. Some output units that saturate produce very small gradients when combined with these cost functions. This is one reason that the cross-entropy cost function is more popular than mean squared error or mean absolute error, even when it is not necessary to estimate an entire distribution $p(y|x)$

Output Units

• 비용함수의 선택은 출력 유닛의 선택과 밀접한 관련이 있다. 대부분의 경우 데이터 분포와 모델 분포 간의 cross-entropy를 사용한다. 출력값을 표현하는 방법은 cross-entropy 함수의 형태를 결정한다.
• 출력으로 사용할 수 있는 모든 종류의 신경망 유닛은 은닉유닛으로도 사용할 수 있다. 여기서는 이러한 유닛을 모델의 출력으로 사용하는 데 중점을 두지만, 원칙적으로는 내부적으로 사용할 수 있다. 섹션 6.3에서 은닉 유닛으로 사용하는 방법에 대한 방법에 대해 자세히 다룰 것이다.
• 이 섹션을 통해서 순방향 신경망이 $\bm{h}=f(\bm{x};\bm{\theta})$로 정의된 은닉 피쳐를 가진다고 가정한다. 출력층의 역할은 피쳐로부터 추가적인 변환을 통해 신경망이 수행해야 하는 작업을 완료한다.

Linear Units for Gaussian Output Distributions

• 비선형성이 없는 affine 변환으로 선형 유닛이라고 불린다.
• 선형 출력유닛은 $\hat{\bm{y}}=\bm{W^\top h+b}$을 생성한다.
• 선형 출력층은 the mean of a conditional Gaussian distribution을 생성한다.
  $p(\bm{y|x})=\mathcal{N}(\bm{y};\bm{\hat{y}},\bm{I})$
• log-likelihood을 최대로 하는 것은 mean squared error을 최소화하는 것과 같다.

Sigmoid Units for Bernoulli Output Distributions

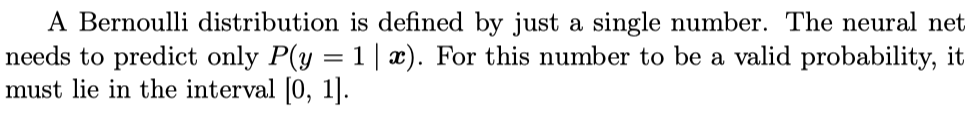
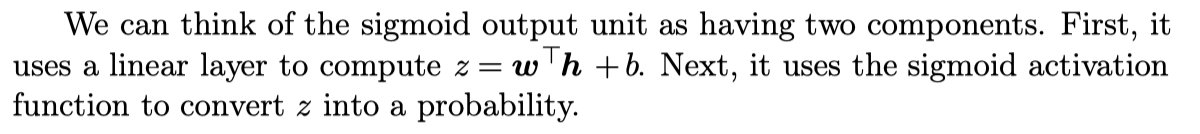
logit

Softmax Units for Multinoulli Output Distributions

• $z=\log\tilde{P}(y=1|\bm{x})$
• a vector $\bm{\hat{y}}$, with $\hat{y_i}=P(y=i|\bm{x})$

• $z_i= \log\tilde{P}(y=i|\bm{x})$

• 소프트맥스는 $\exp$을 취하고 $\bm{z}$을 정규화하여 우리가 원하는 $\bm{\hat{y}}$을 구할 수 있다.

  $\operatorname{softmax}(\bm{z})_i=\frac{\exp(z_i)}{\sum_j\exp(z_j)}$

• maximum log-likelihood

• maximize $\log P(y=i;\bm{z})=\log\operatorname{softmax}(\bm{z})_i$

  $\log\operatorname{softmax}(\bm{z})_i=z_i-\log{\sum_j\exp(z_j)}$

• $\log\operatorname{softmax}(\bm{z})_i$

  • $n$개의 class에 대한 확률분포를 나타내기 위해서 softmax 함수를 사용할 수 있다.
  • $\hat{y_i}=P(y=i|\bm{x})$인 벡터 $\hat{\bm{y}}$를 예측하고자 한다.
    (1) 이때 모든 $\hat{y_i}$은 0과 1 사이의 값이고, 벡터의 합이 1이 되어야 정확한 확률 분포를 나타낼 수 있다.
    (2) Binary의 베르누이 분포와 마찬가지로 Multi-class의 multinoulli 분포에서도 log-likelihood의 gradient 기반 최적화를 하기 위해서 $\hat{\bm{y}}$ 대신 $z_i=\log\tilde{P}(y=i|\bm{x})$인 $\bm{z}=\bm{W^\top h+b}$를 예측한다. 정규화 되지 않은 로그 확률이므로, softmax를 통해 우리가 원하는 $\bm{\hat{y}}$를 얻을 수 있다.
    • $\operatorname{softmax}(\bm{z})_i=\frac{\exp(z_i)}{\sum_j\exp(z_j)}$
  • maximum log-likelihood를 사용하여 소프트맥스를 훈련할 수 있고, 이 때 $\log P(y=i;\bm{z})=\log\operatorname{softmax}(\bm{z})_i$를 최대화 하고자 한다.
    • $\log\operatorname{softmax}(\bm{z})_i=z_i-\log{\sum_j\exp(z_j)}$

• $z_i$과 $\log\sum_j\exp(z_j)$

  • log-likelihood를 최대로 할 때, 첫번째 항은 $z_i$로 하여금 증가하도록 하고, 두번째 항은 모든 $\bm{z}$가 내려가도록 한다.
  • 첫번째 항은 입력값 $z_i$가 항상 비용함수에 직접적으로 기여를 한다는 것을 의미한다. 이 항은 포화되지 않기 때문에 두번째 항에 $z_i$가 기여하는 정도가 매우 작아져도 학습이 계속될 수 있다.
  • 두번째 항인 $\log\sum_j\exp(z_j)$은 대략적으로 $\max_jz_j$로 근사될 수 있다. negative log-likelihood 비용함수가 언제나 가장 잘못된 예측에 대해서 강력하게 페널티를 준다는 것을 알 수 있다.
    • 예를 들어 j번째에 극단적인 오답이 있을 경우, 비용함수는 $z_i-z_j$가 되어 gradient가 linear하게 발생하여 학습이 잘 진행된다.
    • 만약 올바른 답이 이미 softmax의 가장 큰 입력값일 경우, $-z_i$항과 $\log\sum_j\exp(z_j)\approx\max_jz_j=z_i$ 항이 상쇄되어 gradient는 $0$이 될 것이다.
      이러한 샘플의 경우 총 학습 비용함수에 거의 기여하지 않고, 그보다는 아직 올바르게 분류되지 않은 다른 샘플들이 비용함수를 결정한다.

Other Output Types

Hidden Units

how to choose the type of hidden unit to use in the hidden layers of the model.

• Rectified linear units are an excellent default choice of hidden unit.
• Some of the hidden units included in this list are not actually differentiable at { } ( ) 0 all input points.

Rectified Linear Units and Their Generalizations

Rectified linear units use the activation function $g(z)=\max\{0,z\}$

• Rectified linear units are easy to optimize because they are so similar to linear units. The only difference between a linear unit and a rectified linear unit is that a rectified linear unit outputs zero across half its domain. This makes the derivatives through a rectified linear unit remain large whenever the unit is active.
  

Logistic Sigmoid and Hyperbolic Tangent

Other Hidden Units

Architecture Design

###UniversalApproximationPropertiesandDepth
###OtherArchitecturalConsiderations

Back-Propagation and Other Differentiation Algorithms

###ComputationalGraph
###ChainRuleofCalculus
###RecursivelyApplyingtheChainRuletoObtainBackprop
###BackPt-ropagaionComputationinFullyConnectedMLP
###Symbol-to-SymbolDerivatives
###GeneralBack-Propagation
###Example:BackPt-ropagaionforMLPTraining
###Complications
###DifferentiationoutsidetheDeepLearningCommunity
###HigherOrderDerivatives

Historical Notes