글을 작성하게 된 이유:
알고리즘 문제를 풀다보면 소수를 구해야 하는 문제들을 마주하게 됩니다.
소수를 구하는 내용을 풀어봤지만 제대로 알지 못해서 매번 소수를 구하는 방법에 대해서 구글로 향했었습니다...
이를 방지하고 내용을 확실하게 내 것으로 만들기 위해서 글을 작성합니다.
먼저 에라토스테네스의 체를 이해하기 위해서 소수와 소인수분해에 대한 개념을 살펴보고 가겠습니다.
Q. 소수란?
소수는 1보다 큰 자연수 중 1과 자기 자신만을 약수로 가지는 수다.
예를 들어, 5는 1×5 또는 5×1로 수를 곱한 결과를 적는 유일한 방법이 그 수 자신을 포함하기 때문에 5는 소수이다.
(출처: 위키백과)
https://ko.wikipedia.org/wiki/%EC%86%8C%EC%88%98_(%EC%88%98%EB%A1%A0)
또한 1보다큰 자연수중 소수가 아닌 수를 합성수라고 하고, 1은 자연수라고 합니다.
소수의 개수는 무한하며, 이는 유클리드의 정리에 의하여 최초로 논증되었습니다.
유클리드의 정리도 추후에 포스팅 해보겠습니다.
Q. 소인수분해란?
1보다 큰 자연수를 소인수(소수인 인수)들만의 곱으로 나타내는 것 또는 합성수를 소수의 곱으로 나타내는 방법을 말한다.
(출처: 위키백과)
https://ko.wikipedia.org/wiki/%EC%86%8C%EC%9D%B8%EC%88%98%EB%B6%84%ED%95%B4
예를들어, 10이라는 숫자가 있다면 10 = 2 x 5 이렇게 소수의 곱으로 표현 할 수 있습니다.
Q. 에라토스테네스의 체란?
소수를 판별하는 알고리즘으로, 소수들을 대량으로 빠르고 정확하게 구하는 방법입니다.
- 알고리즘
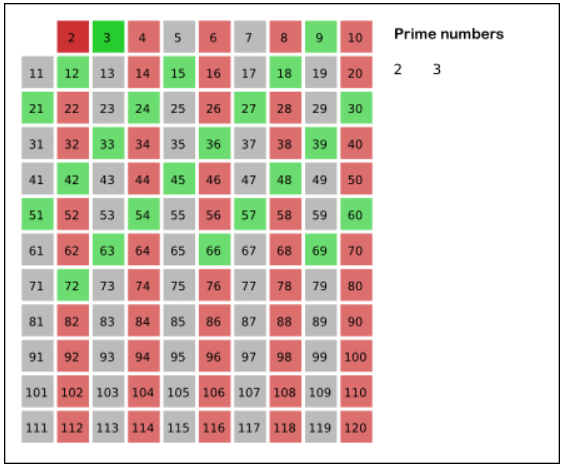
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다.
- 2는 소수이므로 소수 명단에 기록.
- 자기 자신을 제외한 2의 배수를 모두 지운다.
- 남아있는 수 가운데 3은 소수이므로 소수 명단에 기록.
- 자기 자신을 제외한 3의 배수를 모두 지운다.
- 남아있는 수 가운데 5는 소수이므로 소수 명단에 기록.
- 자기 자신을 제외한 5의 배수를 모두 지운다.
- 남아있는 수 가운데 7은 소수이므로 소수 명단에 기록.
- 자기 자신을 제외한 7의 배수를 모두 지운다.
- 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
(출처: 위키백과)
https://ko.wikipedia.org/wiki/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98_%EC%B2%B4
- Java 소스코드
public class Eratos {
public static void main(String[] args) {
// ArrayList로 구현
ArrayList<Boolean> primeList;
// 사용자로부터의 콘솔 입력
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
// n <= 1 일 때 종료
if(n <= 1) return;
// n+1만큼 할당
primeList = new ArrayList<Boolean>(n+1);
// 0번째와 1번째를 소수 아님으로 처리
primeList.add(false);
primeList.add(false);
// 2~ n까지 소수로 설정
for(int i=2; i<=n; i++ )
primeList.add(i, true);
// 2부터 ~ i*i <= n
// 각각의 배수들을 지워간다.
for(int i=2; (i*i)<=n; i++){
if(primeList.get(i)){
for(int j = i*i; j<=n; j+=i) primeList.set(j, false);
//i*i 미만은 이미 처리되었으므로 j의 시작값은 i*i로 최적화할 수 있다.
}
}
StringBuffer sb = new StringBuffer();
sb.append("{");
for(int i=0; i<=n; i++){
if(primeList.get(i) == true){
sb.append(i);
sb.append(",");
}
}
sb.setCharAt(sb.length()-1, '}');
System.out.println(sb.toString());
}
}처리하는 과정의 범위를 루트i까지 하는 이유는 간단한 증명을 통해서 구할 수 있습니다.
우선 직접 체험 해보겠습니다.
예를 들어 10까지 범위에서 소수가 아닌 숫자들을 걸러내고 싶다면, 2부터 반복해 보겠습니다.
10의 제곱근 = 3.XXX
2 -> 4 6 8 10
3 -> 6 9
4 -> 8은 이미 처리되어있다.
정말 10의 제곱근 이하의 범위까지만 돌아도 되네요?
이유는 소수가 아닌 N이 a와 b의 곱이라면(a와 b는 1 혹은 N이 아니다.) a x b = N
(a와 b는 N의 제곱근)으로 표현할 수 있습니다. 만약 a가 N의 제곱근 보다 크다면
N <= a * b 이므로 b <= a 입니다. 즉, 제곱근까지만 검사하면 b와 짝이 되는 a를 포함하여 검사하게 되는 것이고, N이 a와 b의 곱인 것처럼 합성수가 아니라면 소수라고 판별할 수 있는 것입니다.
(참고한 글)
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=sky930425&logNo=221400588919
- 시간 복잡도
O(NloglogN)으로 선형 시간에 가까울 정도로 빠르다.
하지만 각 자연수에 대한 소수 여부를 저장해야 하므로 메모리가 많이 필요하다. - 총평
소수를 구하는 최고의 알고리즘이라고 할 수는 없지만 유명하고 성능도 좋기 때문에 많이 쓰입니다.