
오늘 배운 것
- Time Complexity
- Greedy Algorithm
- Dynamic Programming
들어가기 전에
알고리즘?
알고리즘은 유한한 자원을 가진 공간에서 주어진 문제를 푸는 것을 말한다.
브라우저가 사용할 수 있는 메모리는 일반적인 컴퓨터보다 적다. 자바스크립트가 메모리를 전부 차지해서 OS를 다운시키지 않기 위함이다. 그러나 이 유한한 메모리는 변수 할당, 호출 스택, 스레드에서 할 수 있는 동작에도 제한을 준다.
결론적으로, 알고리즘을 사용한다는 것은 최소한의 메모리만 사용하여 해결하라 라는 뜻이 되겠다.
Time Complexity
시간 복잡도?
알고리즘을 코드로 구현하여 작동시킬 때 공간을 얼마나 차지하는 지 나타내는 지표 중, 시간을 나타내는 지표이다.
시간 복잡도를 통해 알고리즘이 얼마나 효율적인지 알 수 있기 때문에 매우 중요한 요소 중 하나이다.
간단한 용어 정의
시간 복잡도: 수행 시간의 연산을 따지는 것
공간 복잡도: 메모리의 사용량에 따르는 것
연산 횟수를 셀 때 기본적으로 3개의 케이스로 나누어 셀 수 있다.
1. Big-Ω : Best Case
2. Big-θ : Average Case
3. Big-O : Worst Case
이 중 Worst Case가 가장 많이 쓰인다.
배열이나 객체를 탐색하는 것을 예로 들면, 앞쪽 인덱스에서 원하는 결과를 리턴하게 되면 Best Case이지만, 반드시 그러리라는 법은 없다. 중간쯤에서 찾을 수도 있고 마지막에서 찾을 수도 있는데, 맨 마지막에서 찾으면서 그 과정에서 중간에 메모리에 부하를 일으키는 무언가가 포함되어 있다면 그건 정말 Worst Case일 것이다.
Best Case 1개가 있어도 Worst Case 4개가 있다면 Best Case는 무용지물에 가깝기 때문에 Worst Case를 가정하는 것이다.
연산 횟수를 세는 방법
모든 경우의 수를 확인한다
[1, 2, 3, 4, 5, 6, 7, 8, 9]라는 배열이 있다고 가정하고, 가장 큰 수와 가장 작은 수의 차를 구한다고 가정했을 때, 제일 간단하고 귀찮은 방법은 모든 경우의 수를 확인하는 방법일 것이다.
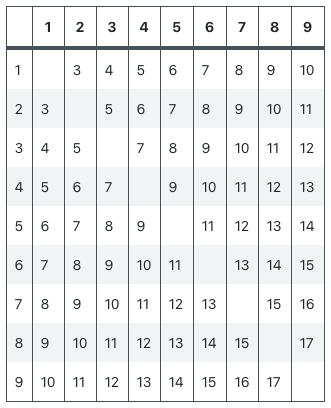
배열에 있는 모든 수를 조합하여 구하고, 두 수의 차를 구하는 방법이다.
배열이 n개라면 배열에 있는 수를 모두 조합하기 위해 n개가 더 필요하다.
이 때문에 이 경우는 n*n, n²가 된다.
가장 큰 수와 작은 수를 찾는다
위와 같은 원시적인 방법을 사용하기 보다 조금 더 스마트한 방법을 사용해 보도록 한다.
가장 큰 수와 가장 작은 수를 구한 뒤 두 수의 차를 계산하는 방법이다.
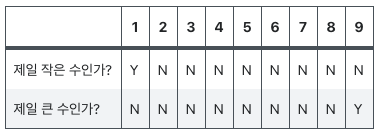
모든 경우의 수를 확인할 때보다 훨씬 연산 수가 줄었다.
배열 n개가 아무리 많아도 가장 작은 수와 가장 큰 수를 찾으면 되기 때문에 n * 2가 되어 2n이 된다.
인덱스를 아는 경우 ?
시간 복잡도를 계산할 때는 항상 우리가 받은 배열이 이미 정렬이 되어 있다고 가정하면, 큰 수와 작은 수를 찾는 과정도 필요 없이 맨 처음과 끝의 인덱스만 빼서 차를 구하면 된다.
이 경우에는 n이 아무리 많이 있어도 3회로 종료된다. 그렇기 때문에 이건 상수로 표기한다.
이것은 constant time이라고 말할 수 있고, 최고의 효율이라고 할 수 있다.
정리

주의 : 2n+n의 경우가 있을 수 있다고 생각할 수 있으나, 지수가 커질수록 상수가 커지는 것이 무의미해지기 때문에 가장 큰 지수를 가진 것만 확인을 한다. (지수가 여러 개 있어도 가장 큰 지수만 사용)
Big-O 표기법의 종류
O(1)
Constant Complexity
입력값이 증가해도 시간은 늘어나지 않음을 의미한다. (딱 한번의 연산을 한 것을 뜻한다)
다르게 말하면, 입력값이 얼마나 커지는지와 관계 없이, 즉시 출력값을 얻어낼 수 있다는 의미이다.
O(n)
Linear Complexity
입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미한다.
배열을 순차적으로 탐색하는 것을 떠올리면 이해가 쉽다.
O(log n)
Logarithmic Complexity
O(1) 다음으로 가장 빠른 시간 복잡도를 가진다. BST라고 생각하면 쉽다.
매번 숫자를 제시할 때마다 경우의 수가 절반이 줄어들기 때문에 빠르게 연산을 종료할 수 있다.
O(n2)
Quadratic Complexity
입력값이 증가함에 따라 시간의 그의 제곱수의 비율로 증가하는 것을 의미한다.
입력값이 1일 때 1초가 걸리던 알고리즘에 5라는 값을 주었더니 25초가 걸리게 되는 케이스이다.
function O_quadratic_algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
// do something for 1 second
}
}
}
function another_O_quadratic_algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
for (let k = 0; k < n; k++) {
// do something for 1 second
}
}
}
}2n, 5n 을 모두 O(n)이라고 표현했던 것과 같은 맥락으로, n^3, n^5 도 모두 Big-O 표기법으로는 O(n2)라 표기한다.
n이 커지면 커질수록 지수가 주는 영향력이 점점 퇴색되어 위와 같이 표기한다.
O(2n)
Exponential Complexity
Big-O 표기법 중 가장 느린 시간 복잡도를 가진다.
재귀를 구현하는 피보나치 수열이 대표적인 케이스이다.
function fibonacci(n) {
if (n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}브라우저 콘솔에서 n을 40으로 입력해도 수 초가 걸리는 것을 볼 수 있으며,
n이 100 이상이 되면 평생 결과를 받지 못할 것이다.
구현한 알고리즘의 시간 복잡도가 이 케이스라면 다른 접근 방식을 고민해 보는 것이 좋다
정리

O(1)은 딱 한 번의 연산을 뜻한다.
O(n)는 2n과 똑같은 연산이다.
O(n^2)는 n²와 같다.
O(n log n)은 average case와 같다.
O(log n)은 BST가 대표적 사례이다. 한 번 순환을 하려고 할 때마다 절반 정도는 보지 않아도 된다.
O(2^n)부터는 최악이기 때문에 반드시 알고리즘의 수정이 필요하다. 보통 재귀함수를 많이 쓸 때 O(n!)이나 O(2^n)이 나오게 된다.
Greedy Algorithm
결정의 순간마다 당장 눈앞에 보이는 최적의 상황만을 쫓아 해답에 도달하는 방법을 말한다.
이러한 탐욕 알고리즘의 문제 해결법을 단계적으로 나누어 보면 아래와 같다
- 선택 절차(Selection Procedure) : 현재 상태에서의 최적의 해답을 선택
- 적절성 검사(Feasibility Check) : 선택된 해가 문제의 조건을 만족하는지 검사
- 해답 검사(Solution Check) : 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 1번으로 돌아가 반복
사용 예시
편의점에서 손님이 4040원을 결제할 때 5000원을 지불하였고, 거스름돈은 동전의 개수를 최대한 적게 요구함
1. 선택 절차 : 동전 개수를 줄이기 위해 가장 가치가 높은 동전을 우선 선택
2. 적절성 검사 : 선택된 동전들의 합이 거슬러 줄 금액을 초과하는지 검사.
2-1. 초과할 경우 : 가장 마지막에 선택한 동전을 삭제, 1번으로 돌아가 한 단계 작은 동전을 선택
2-2. 초과하지 않을 경우 : 3번으로 넘어감
3. 해답 검사 : 선택된 동전들의 합이 거슬러 줄 금액과 일치하는지 검사. 부족할 경우 1번으로 돌아가 반복
탐욕 알고리즘은 문제를 해결하는 과정에서 매 순간마다 최적이라 생각하는 해답을 찾으며, 이를 토대로 최종 문제의 해답에 도달하는 문제 해결 방식이다. 하지만 항상 최적의 결과를 보장하지는 못한다
따라서 탐욕 알고리즘을 사용하려면 일정 조건을 성립하여야 잘 작동한다.
즉, 일정 조건을 만족하는 특정한 상황이 아니면 탐욕 알고리즘은 최적의 해를 보장하지 못한다.
- 탐욕적 선택 속성 : 앞의 선택이 이후의 선택에 영향을 주지 않음
- 최적 부분 구조 : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성
항상 최적의 결과를 도출하는 것은 아니지만, 어느 정도 최적해에 근사한 값을 빠르게 도출할 수 있기 때문에 근사 알고리즘으로 사용이 가능하다.
Dynamic Programming
탐욕 알고리즘과 늘 함께 언급되는 알고리즘. 동적 계획법이라고 부른다.
탐욕 알고리즘이 순간의 최적을 찾는 방식이라면, 동적 계획법은 모든 경우의 수를 따져본 후 이를 조합해 최적의 해법을 찾는 방식이다.
원리
주어진 문제를 여러 개의 하위 문제로 나누어 풀고, 하위 문제들의 해결 방법을 결합하여 최종 문제를 해결
하위 문제를 계산하고 해결책을 저장하여, 같은 문제가 다시 나왔을 경우 저장된 해결책을 이용하여 계산 횟수를 줄임으로써 비효율적인 알고리즘을 개선하는 방식. 우리 몸의 면역체계 같은 느낌인데?
요약하자면, 하나의 문제는 딱 한번만 풀도록 하는 알고리즘이다.
사용 조건
- 큰 문제를 작은 문제로 나눌 수 있고, 이 작은 문제들은 중복된다.
- 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 같다. 즉, 작은 문제에서 구한 정답을 큰 문제에서도 사용할 수 있다.
사용 예시 1
첫 번째 조건을 바꾸어 말하면
큰 문제로부터 나누어진 작은 문제는, 큰 문제를 해결할 때 여러번 반복해서 사용될 수 있어야 한다
피보나치 수열을 예로 들면, 첫째와 둘째 항이 1이며, 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다.
이를 재귀로 구현하면 아래와 같다.
function fib(n) {
if(n <= 2) return 1;
return fib(n - 1) + fib(n - 2);
}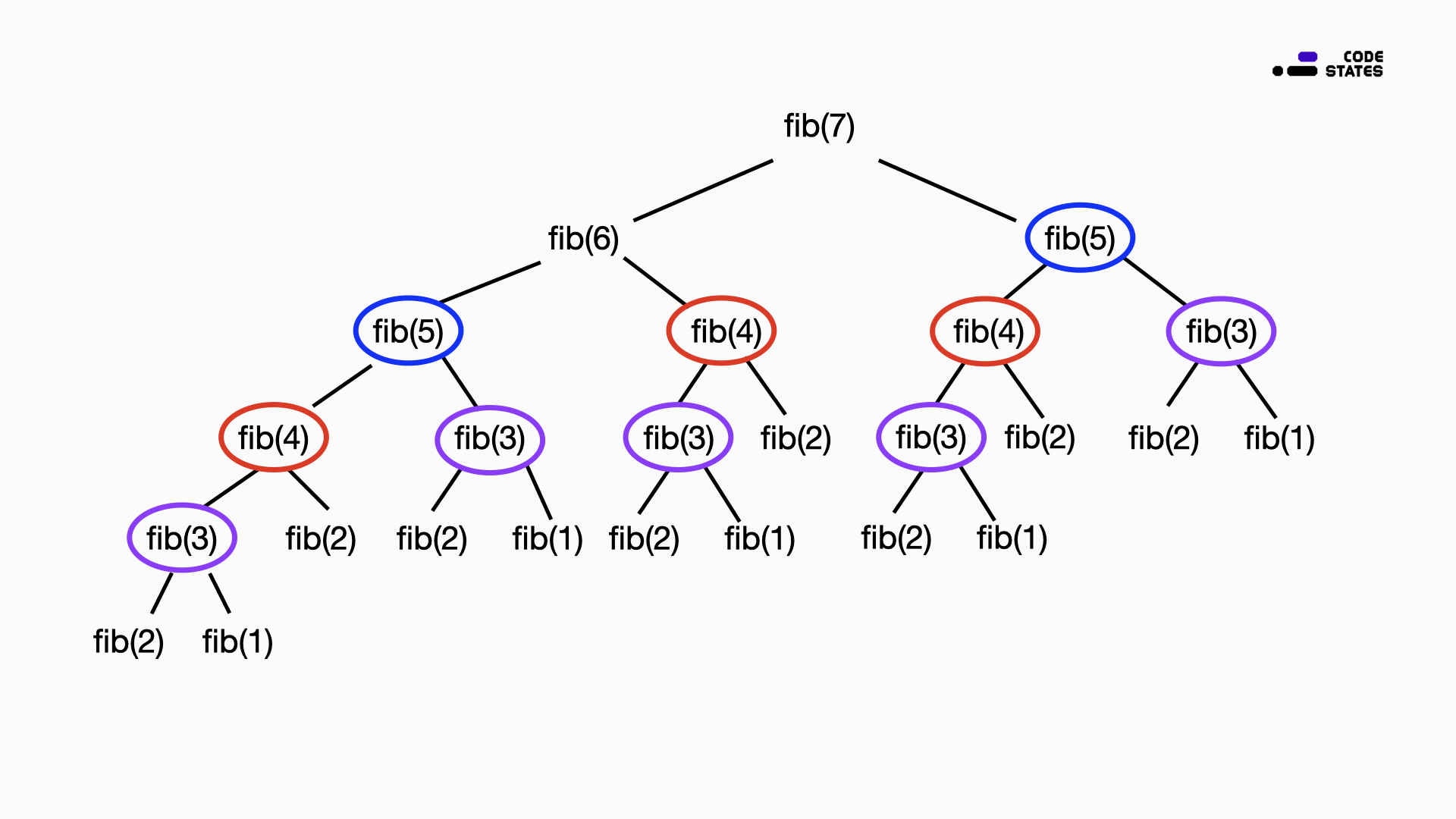
이 예시와 같이 동일한 계산을 반복적으로 수행해야 하고, 이 과정 안에서 fib(5), fib(4), fib(3)은 동일한 계산을 반복해야 한다는 것을 알 수 있다.
주의할 점은, 주어진 문제를 단순 반복 계산하여 해결하는 것이 아니라, 작은 문제의 결과가 큰 문제를 해결하는 데에 여러번 사용될 수 있어야 한다.
사용 예시 2
두 번째 조건을 바꾸어 말하면
주어진 문제에 대한 최적의 해법을 구할 때, 그것의 작은 문제들의 최적 해법을 찾은 후 결합하면 된다
아래와 같은 지점이 있고, 한 지점에서 다른 지점으로 갈 수 있는 경로와 해당 경로의 거리가 아래와 같다고 할 때, A에서 D로 가는 최단 경로는 ?
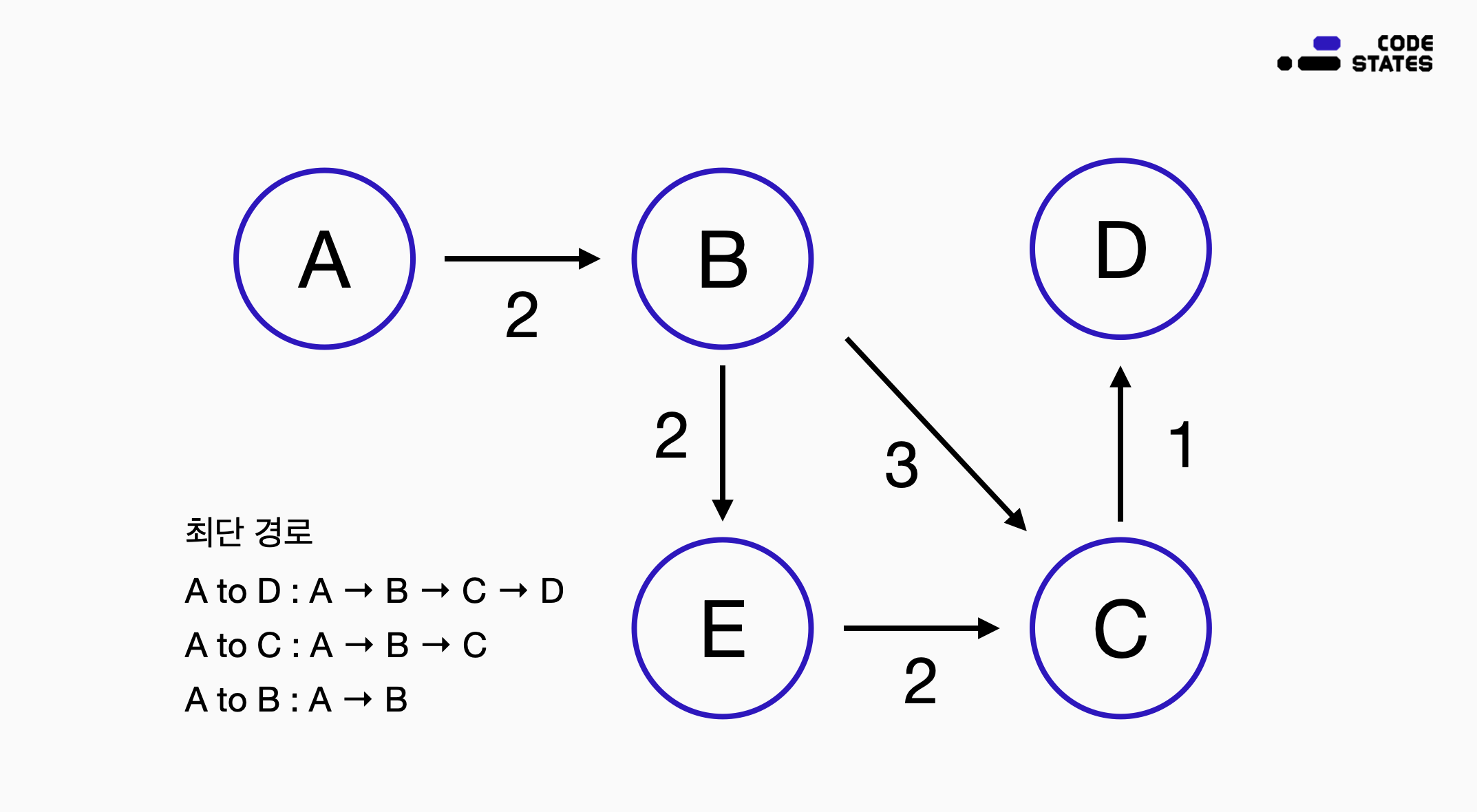
A to B의 최단 경로 : A - B
A to C의 최단 경로 : A - B - C
A to D의 최단 경로 : A - B - C - D
A부터 D까지의 최단 경로를 구하기 위해 A - B와 A - B - C 를 결합하여 찾았다.
위와 같이 다이내믹 프로그래밍을 적용하기 위해서는 작은 문제들의 최적 해법을 결합하여 최종 문제의 최종 해법을 구할 수 있어야 한다.
피보나치 수열에서의 적용
Recursion + Memoization
Memoization : 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장하여 반복 수행을 제거. 실행 속도를 빠르게 하는 기술
function fibMemo(n, memo = []) {
if(memo[n] !== undefined) return memo[n];
// 이미 해결한 하위 문제인지 찾아본다
if(n <= 2) return 1;
let res = fibMemo(n-1, memo) + fibMemo(n-2, memo);
// 없다면 재귀로 결과값을 도출하여 res 에 할당
memo[n] = res;
// 추후 동일한 문제를 만났을 때 사용하기 위해 리턴 전에 memo 에 저장
return res;
}피보나치를 구하기 위해서는 앞서 저장해 놓은 하위 문제들의 결과값을 가져다 사용하면 되며,
n이 커질수록 계산해야 할 과정은 선형으로 늘어나기 때문에 시간 복잡도는 O(N)이 된다.
Memoization을 사용하지 않고 재귀로만 문제를 풀 경우 n이 하나 커질수록 계산해야 할 과정이 2배씩 늘어나기 때문에 시간복잡도가 O(2^N)이 되는 것과 비교할 경우 굉장한 시간 절약이 가능하다.
이 방식을 Top-down이라 칭하기도 한다. (저장된 작은 케이스를 호출하는 방식이 마치 위에서 아래로 내려가는 형태와 같기 때문)
Iteration + Tabulation
반복문을 이용하는 방법
function fibTab(n) {
if(n <= 2) return 1;
let fibNum = [0, 1, 1];
// n 이 1 & 2일 때의 값을 미리 배열에 저장해 놓는다
for(let i = 3; i <= n; i++) {
fibNum[i] = fibNum[i-1] + fibNum[i-2];
// n >= 3 부터는 앞서 배열에 저장해 놓은 값들을 이용하여
// n번째 피보나치 수를 구한 뒤 배열에 저장 후 리턴한다
}
return fibNum[n];
}하위 문제의 결과값을 배열에 저장해 놓고 필요할 때 꺼내 쓰는 개념은 재귀와 같으나,
재귀는 문제를 해결하기 위해 큰 문제부터 시작하여 작은 문제로 옮겨가며 문제를 해결하였다면,
반복문은 작은 문제부터 시작하여 큰 문제로 옮겨가며 문제를 해결하는 방법이다.
이 때문에 Bottom-up 이라 칭하기도 한다.
