구간 나누기 2 13397

https://www.acmicpc.net/problem/13397

완전탐색으로 할 수 있을까 시간복잡도를 대충 계산해보면 5000 개 숫자
몇개의 구간으로 나누든 구간안에서 최대 최소를 탐색 해야한다 그럼 5000
그리고 구간을 1로 나누는건 의미 없으니 2로 나눈다하면둘로 나뉠수 있는 경우의수도 5000
그럼 5000^3 으로 생각되어서 완전탐색은 안될듯하다
풀이를 보아도 이해가 잘 되지 않는다 대략적인 이해는 되는데 막상 구현해보니 계속 틀려서 몇번을 수정해서 풀었다.

알고리즘 스터디를 하면서 이해하게 되었다

8 3
1 5 4 6 2 1 3 7

첫번째 예제를 사용해서 이해해보자. 입력 숫자들 중 가장 큰 숫자는 7 이므로 0~7의 숫자범위를 가진다고 하고 변수를 세팅한다
left=0
right=7
left+right / 2 = 3
중간값은 3 이다. candidate 3 이라고 변수를 사용하였다.

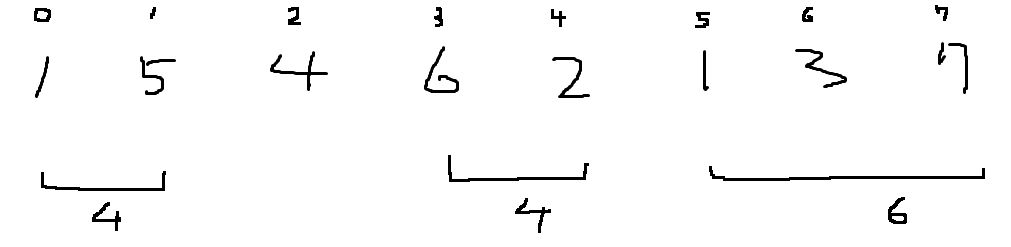
그림을 보면서 알고리즘을 돌려보자
for문을 돌리면서 min, max 값을 갱신한다. 갱신하면서 diff = max - min 값을 구한다
min, max가 i = 0 일때 1, 1 => diff = 0
i = 1 일때 1, 5 => diff = 4
diff(4) > candidate(3) 이므로 구간을 분리한다 왜냐면 1과 5가 같은 구간에 있으면 최대값 4가 나오고 이것은 3보다 크니까

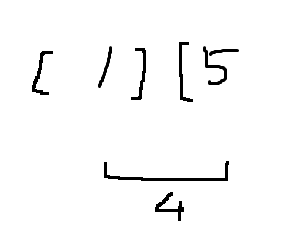
그리고 min, max 는 5, 5로 세팅한다
i = 2 일때 min, max 는 4, 5 => diff = 1 이므로 다음순회
i = 3 일때 min, max 는 4, 6 => diff = 2 이므로 다음순회
i = 4 일때 min, max 는 2, 6 => diff = 4 이므로
diff(4) > candidate(3) 이므로 구간을 분리한다

계속하다보면
i = 7 일때
diff(6) > candidate(3) 이므로 구간을 분리한다

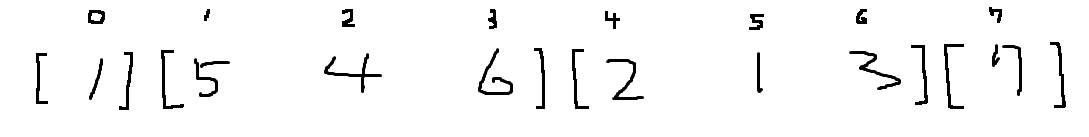
총 4개의 구간이 되는것을 알 수 있다. 이것은 입력된 구간 3 보다 크므로 candidate(3)의 값을 높여야한다
최대값을 올리면 구간은 작아진다(?) 라고 생각해서 그런듯;
그래서 left = candidate(3)+1 을 한다

그람 다시 첨부터 candidate(5) = left(4)+ right(7) / 2 를 하면서
for 문 돌리면서 반복해주면 된다...

이분탐색 이므로 숫자의 최대크기 10000 * log 10000 약 4만번이 아닐까 생각해봄

import java.io.*;

public class Main
{
    static int N;
    static int M;

    public static void main(String[] args)throws  IOException
    {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        String[] input = br.readLine().split(" ");

        N = Integer.parseInt(input[0]);
        M = Integer.parseInt(input[1]);
        int[] arr = new int[N];

        input = br.readLine().split(" ");
        int right = Integer.MIN_VALUE;
        for(int i = 0; i < N; ++i)
        {
            arr[i] = Integer.parseInt(input[i]);
            right = Math.max(right, arr[i]);
        }

        int left = 0;

        int candidate = 0;

        while(left < right)
        {
            candidate = (left + right) / 2;

            int diff;
            int min = Integer.MAX_VALUE;
            int max = Integer.MIN_VALUE;
            int cnt = 1;
            for(int i = 0; i < N; ++i)
            {
                min = Math.min(min, arr[i]);
                max = Math.max(max, arr[i]);
                diff = max-min;

                if(diff > candidate)
                {
                    cnt++;
                    min = arr[i];
                    max = arr[i];
                }
            }

            if(cnt > M )
            {
                left = candidate+1;
            }
            else if(cnt <= M)
            {
                right = candidate;
            }
        }

        System.out.println(right);
    }
}