이 내용은 Introduction to Algorithm 책에나온 목차순으로 정리하기 위해 작성했음을 알립니다.

Red-Black Trees

13.1 red-black trees의 속성

레드-블랙 트리는 각 노드가 추가 bit의 정보를 가지는 이진탐색트리이다. 각 노드의 색: 레드-블랙 둘중 하나. root-leaf의 simple path에 따라 각 노드의 색을 제한(결정)하고 이를 통해서 red-black tree는 simple path보다 2배를 초과하는 경로가 없음을 보장한다. 그렇기 때문에 레드-블랙 트리는 대체로(Approximately) 균형이 잡혀있다.

그래서 레드-블랙 트리의 높이는 노드가 N일 때 최대 2log(N + 1) 이며 이는 O(logN)으로 나타낼 수 있다.

각 노드는 color, key, left, right, parent를 요소로 가지고 있다. 만약 자식노드나 부모노드가 없을경우 각 포인터는 NIL의 주소값을 가진다. NIL은 BST(이진탐색트리)의 리프노드(external nodes)로, 키가 입력된 노드는 내부의 노드로 생각하자.

레드-블랙 트리는 이진 검색 트리 이며 다음과 같은 red-black properties를 만족한다.
1. 모든 노드는 빨강 or 검정이다.
2. 루트 노드는 검정이다.
3. 모든 리프 노드(NIL)은 검정이다.
4. 만약 한 노드가 빨강이면 자식노드는 모두 검정이다.
5. 각각의 노드는 모든 아래로 내려가는 경로(descendant leaves)위에 존재하는검정노드의 수가 같다. (black height가 모두 같다고 한다)

5번 조건이 중요한데 어떠한 노드를 선택했을 경우 leaf node(NIL)에 도달할 때까지의 경로에서 만나는 검정노드의 개수가 모두 동일해야 한다는 뜻이다.

• 코드구현 case 1: nil노드를 sentinel node로 사용할 경우
  모든 NIL노드는 단 하나의 sentinel node로 표현되며 사용된 NODE는 red-black tree의 root노드와 함께 보관된다. (여기서 사용하는 코드상으로는 구조체로 함께 저장된다). NIL노드의 색은 검정이며

• 코드구현 case 2: nil노드를 선언하는 대신 NULL로 사용할 경우
  노드의 존재하지 않음을 NULL로 처리하기 때문에 각 NIL노드는 주소값을 가지지 않는다(NULL값을 가진다 혹은 가리킨다)

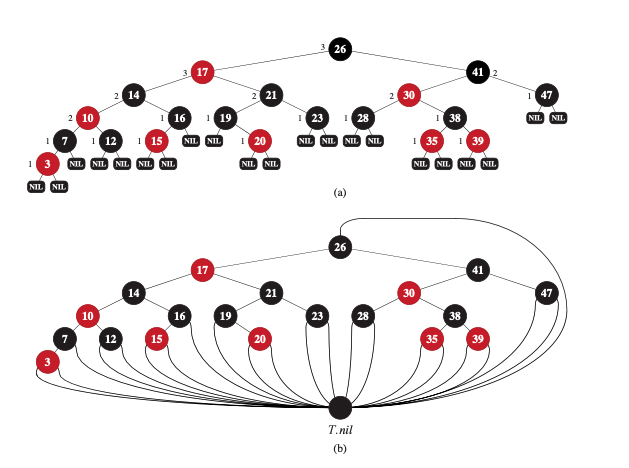
왜 센티넬(sentinel) 노드를 사용하는가?

센티넬 노드를 사용할 경우 어떠한 노드 x의 자식노드인 NIL을 평범한 노드로 취급한다. 이러한 디자인 대안(Alternative design)은 각각의 NIL노드를 별개로 취급하여 사용할 수 있으며 각 NIL노드의 부모가 제대로 정의될 수 있다.

• 센티넬 노드로 선언된 NIL은 트리별로 다르게 가질 수 있으므로 개별로 취급할 수 있고 각 트리안에서 NIL노드를 자식노드로 가지는 유효한(ordinary) 노드들을 잘 정의할 수 있도록 해준다.
• NULL을 나타내지 않기 때문에 NULL pointer exception같은 위험에서 벗어날 수 있다고 해석했다.

트리의 전체 높이

각 자식 노드의 내부의 노드(internal nodes, 자식노드들)의 개수는 적어도 2^bh(x)-1 - 1 개의 노드를 가진다.
그렇다면 양쪽 서브트리에 루트노드를 더하면
(2^bh(x)-1 - 1) + (2^bh(x)-1 - 1) + 1 = 2^bh(x) - 1 로 나타낼 수 있다.

h를 트리의 높이, n을 노드의 전체 개수라고 하자.
red-black tree의 속성 4번에 따라 각 왼쪽, 오른쪽 서브트리는 루트를 제외하고는 적어도 절반은 검은색 노드이여야 한다. (black-height는 NIL노드의 영향을 받는다)

그렇기 때문에 루트의 black-height는 반드시 h/2 이상이어야 한다.
그러므로 n >= 2^h/2 - 1이 성립한다.

여기서 양번에 1을 더하고 밑변이 2인 로그를 취하면 log(n+1) >= h/2 이며
결론적으로 h <= 2log(n+1)이 성립됨을 알 수 있다.

시간복잡도 O(logn)

위에서 도출된 결과로 보아 탐색(search), 최소값(minimum), 최대값(maximum), 중위 선행자(successor), 중위 후행자(predecessor) 연산의 시간복잡도는 O(logn)임을 알 수 있다.

삽입(insert), 삭제(delete)연산을 제외한 위의 연산들은 BST의 연산과 동일하며 같은 시간복잡도인 O(logn)로 표현된다.

회전(Rotation)

레드-블랙 트리의 삽입, 삭제 연산은 O(logn)의 시간복잡도를 가진다. 트리를 수정하는 과정에서 레드-블랙 트리의 속성을 위반할 수 있기 때문이다. 이를 고치기 위해서는 color와 노드의 pointer들을 수정할 필요가 있다.

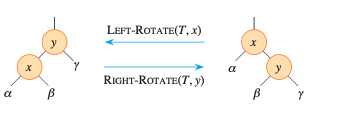
이는 rotation이라는 local opertaion을 통해 이루어지며 두가지 경우가 있다. 왼쪽 회전, 오른쪽 회전

insert_fixup

레드-블랙 트리의 속성을 유지하기 위해서 노드 삽입후 진행하는 과정이다.
rotation을 적절히 사용하고, color를 변경해줌으로써 red-black tree의 properties 를 유지할 수 있게 해준다.

큰 틀에서 보면 Case 1, 2, 3 으로 나뉘며 case2와 case3는 상호베타적(mutual exclusive)이 아니다 -> case2는 반드시 case3를 거치게 된다. (case 2 falls through in to case 3)

fixup이 진행되면서 5개의 속성 중 어떤 속성이 위반될까?
1: black or red
2: root is black
3: NIL is black
4: no red-red
5: same black-height

2번, 4번이 위반될 소지가 있다. 새로 삽입된 노드는 항상 빨간색 노드 이므로. 단 2번 혹은 4번을 동시에 위반하지는 않는다. 2번의 경우 새로운 노드가 루트노드일때 발생하고, 4번의 경우 새로운 노드의 부모가 빨간색일 경우 이므로 둘 중 하나만 위반하게 된다.