[APS] 그래프 심화(3)

Bzeromo·2023년 9월 22일

APS 그래프 위상 정렬

APS

목록 보기

21/23

⚡ 그래프 심화 (3)

📌 위상 정렬(Topological Sorting)

🔷 순서가 있는 작업을 차례로 진행해야 할 때 순서를 결정해 주기 위해 사용하는 알고리즘

사이클이 없는 방향 그래프의 모든 노드를 주어진 방향성에 어긋나지 않게 순서를 나열하는 것
만들 수 있는 순서의 나열이기 때문에 여러 경우가 등장할 수도 있다.

🔷 유향 비사이클 그래프(Directed Acyclic Graph, DAG)에 한해 가능하다.

유향 그래프이면서 사이클이 존재하지 않는 그래프

🔷 진입 차수(in-degree): 특정 노드로 들어오는 간선의 개수

🔷 진출 차수(out-degree): 특정 노드에서 나가는 간선의 개수

💡 위상 정렬을 위해 꼭 필요한 차수는 진입 차수이다.

⭐ Queue로 구현하기

🔷 방법

1) 진입 차수가 0인 모든 노드를 큐에 삽입한다.

2) 큐가 공백상태가 될 때까지 반복 수행한다.

큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거한다.
(연결 된 노드의 진입 차수를 감소 시킨다.)
새롭게 진입 차수가 0이 된 노드를 큐에 삽입한다.

💡 Queue에서 꺼내지는 순서(Queue 들어온 순서)가 위상 정렬을 수행한 결과이다.'

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class DailyAPS {
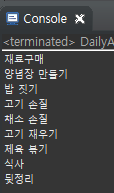
	public static String[] cook = {"", "재료구매", "양념장 만들기", "고기 재우기", "고기 손질", "제육 볶기", "식사", "뒷정리", "채소 손질", "밥 짓기" };
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(input);
		
		int V = sc.nextInt();
		int E = sc.nextInt();
		
		//인접행렬
		int [][] adjArr = new int[V + 1][V + 1]; //1번 정점부터 시작해서 V번까지
		int [] degree = new int [V + 1]; //진입차수를 저장할 배열
		
		for(int i = 0; i < E; i++) {
			int A = sc.nextInt();
			int B = sc.nextInt();
			
			//유향그래프
			adjArr[A][B] = 1; //가중치가 따로 주어지지 않았기 때문에
			//진입차수를 증가
			degree[B]++;
		}
		
		//degree가 0인 정점만 들어갈 수 있는 큐 준비
		Queue<Integer> queue = new LinkedList<>();
		
		//초기에 진입차수가 0인 정점을 모두 큐에 넣기
		for(int i = 1; i < V+1; i++) {
			if(degree[i] == 0)
				queue.add(i);
		}
		
		while(!queue.isEmpty()) {
			int work = queue.poll(); //현재 작업하나 꺼낸다.
			
			System.out.println(cook[work]); //작업 출력
			
			for(int i = 0; i < V+1; i++) {
				if(adjArr[work][i] == 1) {
					adjArr[work][i] = 0; //간선 제거, 없어도 정답 출력에는 지장없음
					degree[i]--; 		 //진입차수 감소
					
					if(degree[i] == 0)	 //진입차수가 0이라는 것은 선행 작업이 모두 완료되었다는 것,
						queue.add(i); 	 //큐에 들어가도 좋다.
				}//연결확인
			}//연결 끊는 작업
			
		}
	}
	
	
	public static String input = "9 9\r\n" + "1 4\r\n" + "1 8\r\n" + "2 3\r\n" + "4 3\r\n" + "8 5\r\n" + "3 5\r\n"
			+ "5 6\r\n" + "9 6\r\n" + "6 7\r\n" + "";
}

⭐ Stack으로 구현하기

🔷 방법

1) 진입 차수가 0인 모든 노드에서 DFS 탐색을 수행한다.

2) DFS 수행 시

해당 노드를 방문 표시
인접하면서 방문하지 않은 노드가 있다면 DFS 재귀 호출
함수 리턴 하기 전 Stack에 현재 노드 저장

3) Stack이 공백 상태가 될 때까지 pop한다.

💡 Stack에서 꺼내지는 순서를 뒤집으면 위상 정렬을 수행한 결과이다.

import java.util.Scanner;
import java.util.Stack;

public class DailyAPS {
	public static String[] cook = {"", "재료구매", "양념장 만들기", "고기 재우기", "고기 손질", "제육 볶기", "식사", "뒷정리", "채소 손질", "밥 짓기" };
	
	static int V, E;
	static int [][] adjArr;
	static int[] degree;
	static boolean[] visited;
	static Stack<Integer> stack;
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(input);
		
		V = sc.nextInt();
		E = sc.nextInt();
		
		//인접행렬
		adjArr = new int[V + 1][V + 1]; //1번 정점부터 시작해서 V번까지
		degree = new int [V + 1]; //진입차수를 저장할 배열
		visited = new boolean [V + 1];
		stack = new Stack<>();
		
		for(int i = 0; i < E; i++) {
			int A = sc.nextInt();
			int B = sc.nextInt();
			
			//유향그래프
			adjArr[A][B] = 1; //가중치가 따로 주어지지 않았기 때문에
			//진입차수를 증가
			degree[B]++;
		}
		
		//진입차수가 0인 원소들을 가지고 출발한다
		for(int i = 1; i < V+1; i++) {
			if(degree[i] == 0) 
				DFS(i);
		}
		
		while(!stack.isEmpty()) {
			System.out.println(cook[stack.pop()]);
		}
		
	}
	
	private static void DFS(int v) {
		visited[v] = true; //현재 정점 방문 체크
		
		for(int i = 1; i < V+1; i++) {
			//인접하지만 방문하지 않은 정점들을 방문
			if(adjArr[v][i] == 1 && !visited[i]) {
				DFS(i); //깊이우선탐색
			}
		}
		
		stack.add(v);
	}
	
	public static String input = "9 9\r\n" + "1 4\r\n" + "1 8\r\n" + "2 3\r\n" + "4 3\r\n" + "8 5\r\n" + "3 5\r\n"
			+ "5 6\r\n" + "9 6\r\n" + "6 7\r\n" + "";
}