https://school.programmers.co.kr/learn/courses/30/lessons/12929
문제 설명
올바른 괄호란 (())나 ()와 같이 올바르게 모두 닫힌 괄호를 의미합니다. )(나 ())() 와 같은 괄호는 올바르지 않은 괄호가 됩니다. 괄호 쌍의 개수 n이 주어질 때, n개의 괄호 쌍으로 만들 수 있는 모든 가능한 괄호 문자열의 갯수를 반환하는 함수 solution을 완성해 주세요.
- 괄호 쌍의 개수 N : 1 ≤ n ≤ 14, N은 정수
문제 해결 방법
두 가지 방법이 생각났다.
- (, ) 쌍을 개수만큼 준비해서 모든 조합을 대상으로 괄호가 올바르게 정렬되었는지 완전 탐색한다.
- 점화식을 찾아서 dp로 해결한다.
1번의 최악의 경우를 생각할 때 깊게 생각할 필요 없이 대충 (, ) 개수 조건 없이 각 자리마다 둘 중 하나 선택하는 식으로 경우의 수를 계산하면,
- 2의 14승 * 14 (각 문자를 순서대로 탐색해 (이 나오면 큐에 넣고, )가 나오면 큐에서 하나씩 제거하는 식으로 판별)
물론 이거보다 적은 시간이 걸리겠지만 상당히 오래걸리므로 풀이 방법에서 제외했다.
따라서 이 문제는 점화식만 찾는다면 dp로 해결해야 한다는 결론에 도달했다.
점화식을 세우기 위해 비교적 관찰이 쉬운 n=1, 2, 3일때를 보자.
- ()
- () (), (())
- () () (), (()) (), () (()), (() ()), ((()))
다음과 같이 다섯개다.
n=3 일 때를 보면 경우의 수에 대한 규칙은 다음과 같다.
- n=2 일 때에 괄호를 하나 더 감싼다
- n=2 일 때 오른쪽에 n=1 일 때를 추가한다.
- n=1 일 때 오른쪽에 n=2 일 때를 추가한다.
근데 이러면 () () ()가 중복된다.
중복을 피하기 위해 중복 위험이 있는 괄호의 개수를 따로 저장하는 방법이 있을 수 있다.
일단 이 방법은 구현이 복잡해질 것 같아서 제외했다.
새로운 점화식을 떠올리기 위해 주의 깊게 봐야할 점은 '이전 경우의 수들에 괄호 하나를 어떻게 추가하느냐'이다.
즉 어떻게 경우의 수를 합치든 반드시 괄호 하나 () 가 더 존재해야하고 이 괄호를 기준으로 이전 값들을 이용해야한다.
생각해보면 다음과 같이 생각할 수 있다.
dp[i]는 괄호 i쌍일 때 경우의 수라고 하자. n=k 일 때,
- (dp[k-1])
- (dp[k-2]) dp[1]
... - (dp[1]) dp[k-2]
- () dp[k-1]
새로운 괄호를 왼쪽에 두고 안과 밖을 나눈 기준으로 계산하면 모든 경우가 distinct하게 나온다.
즉 '처음 나오는 괄호 안에 있는 괄호 경우의 수 X 그 다음 나오는 괄호들의 경우의 수'가 정답이다.
이해가 어렵다면 울타리 문제를 생각해보자.
괄호 4개를 사용할 때 경우의 수는 다음과 같다.
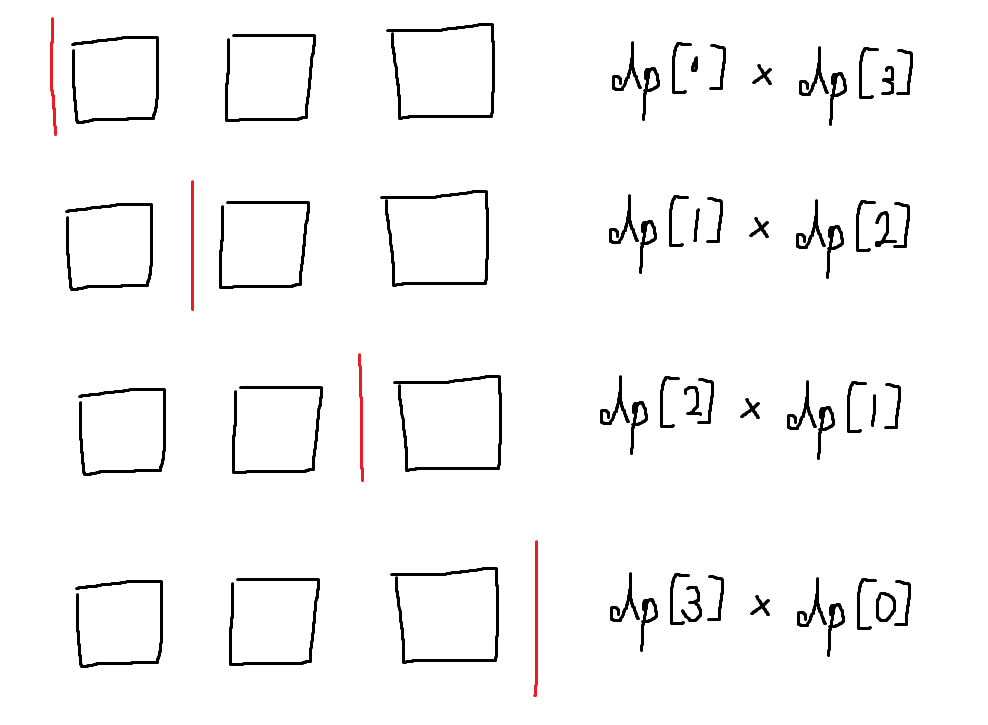
네모를 괄호 세트라고 하면 빨간색 울타리를 기준으로 양 옆으로 만들 수 있는 괄호 경우의 수를 곱하면 된다.
코드 구현
def solution(n):
answer = 0
dp = [0 for _ in range(n+1)]
dp[0] = 1
dp[1] = 1
for t in range(2, n+1):
for i in range(t):
f, s = i, t-i-1
dp[t] += dp[f] * dp[s]
answer = dp[n]
return answer느낀점
점화식을 얻기 위해 고민할 땐 고등 수학 풀듯이 경우의 수를 나열해보고 어떤 n=k에 대해서 어떻게 이 경우의 수가 구성되었는지 고민할 필요가 있다.
