https://school.programmers.co.kr/learn/courses/30/lessons/64064
문제설명
사용자 리스트와 와일드 카드가 섞인 불량 사용자 리스트를 입력받고, 불량 사용자가 될 수 있는 조합의 개수를 구하는 문제이다.
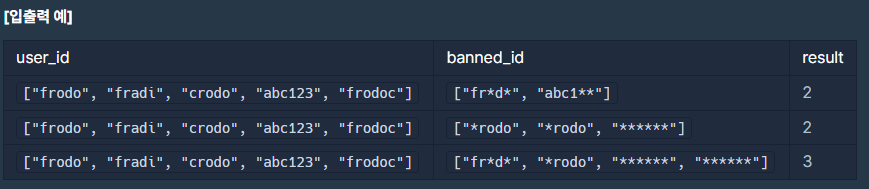
세 번째 예시를 보면 가능한 조합은 다음과 같다.
- frodo, crodo, abc123, frodoc
- fradi, frodo, abc123, frodoc
- fradi, crodo, abc123, frodoc
한 조합에서 같은 아이디는 2개 이상의 불량 사용자 아이디와 매칭될 수 없다. 두 리스트 모두 최대 길이는 8이며 문자열의 최대 길이는 8이다.
문제 해결 방법
문제가 많이 까다롭다. 특이한 점은 리스트 길이와 문자열 길이 모두 최대 8 이다.
차단당한 아이디마다 가능한 모든 아이디의 인덱스를 배열에 저장하고 이를 조합하는 형식의 완전 탐색을 생각해볼 수 있다.
위 예시에서는 인덱스를 저장한 배열은
[[0, 1], [0, 2], [3, 4], [3, 4]]
다음과 같고, 이를 완전탐색으로 모두 탐색한다면
0033, 0034, ..., 1234, 1243, 1244이다.
해결할 때 주의해야 할 부분은 두 부분이였다.
- [1, 2, 3, 4]와 [1, 2, 4, 3]은 같은 조합이다.
- 대충 O(N^M) 이상의 시간 복잡도가 예상된다.
첫 번째 부분은 인덱스를 정렬한 뒤 문자열로 변환해 set에 담으면 중복을 제거할 수 있다는 생각이 든다.
하지만 정렬까지 사용한다면 대충 생각해도 8log8 * 8^8 이니까 이 값은 내가 항상 어림잡아 목표하는 수치인 1억을 넘어간다.
BFS에서 더 이상 시간복잡도를 줄이는 방법을 고려할 순 없을 때 가지치기(Backtracking)를 사용할 수 있다.
가지치기 또한 완전 탐색이지만 이 문제의 경우 탐색 중간 중간에, 정답에 불가능한 조합을 미리 잘라낼 수 있다.
이 방식대로 한다면 banned_id 리스트의 길이가 절반보다 커질수록 더 많이 가지치기 할 수 있다.
코드 구현
def solution(user_id, banned_id):
def bt(prunList, l, n):
if l == n:
temp = sorted(prunList)
s.add("".join(map(str, temp)))
return
for i in cases[l]:
if i not in prunList:
prunList.append(i)
bt(prunList, l+1, n)
prunList.pop()
cases = [[] for _ in range(len(banned_id))]
answer = 0
s = set()
pl = []
for idxB, bId in enumerate(banned_id):
for idxU, uId in enumerate(user_id):
check = 0
bIdLen = len(bId)
if bIdLen != len(uId):
continue
for i in range(bIdLen):
if bId[i] == '*':
check += 1
elif bId[i] == uId[i]:
check += 1
if check == bIdLen:
cases[idxB].append(idxU)
print(cases)
bt(pl, 0, len(cases))
answer = len(s)
return answer후기
처음에 가지치기를 사용하지 않고 그대로 탐색했을 때 시간초과가 났다. 대략적으로라도 시간 복잡도를 계산하는 습관을 반드시 들여야 한다.
백트래킹의 pseudocode를 기억하자. 완전탐색에서 많이 쓰니까.
