https://www.acmicpc.net/problem/2352
문제 설명
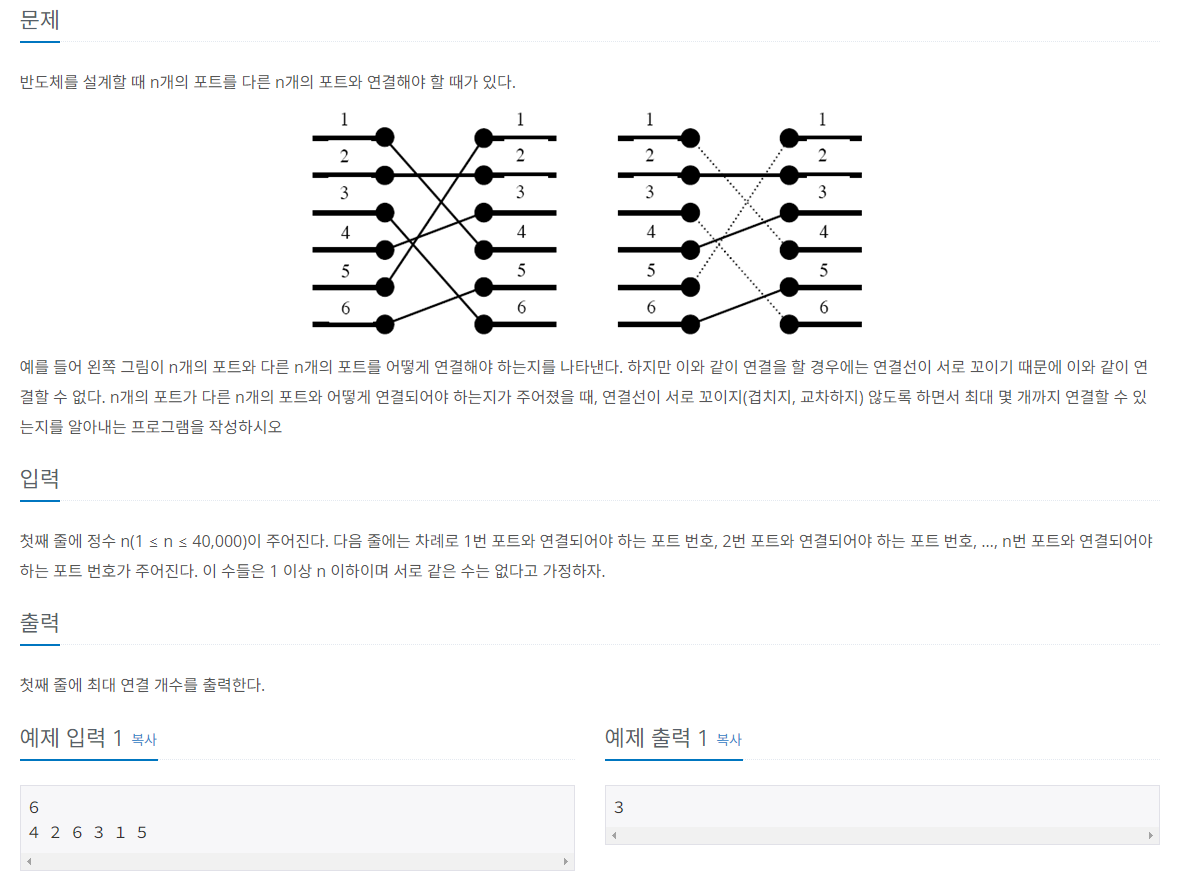
문제 해결 방법
처음엔 그리디한 방식이 먼저 떠올라서 풀었다가 틀렸다.
왼쪽 오른쪽 상관없이 둘 중 큰 값을 기준으로 정렬한 뒤 조건을 만족하는 차례대로 세면 정답이지 않을까? 생각했다.
즉 위 예시대로 한다면 처음 입력한 배열엔
| idx | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 4 | 2 | 6 | 3 | 1 | 5 |
대충 이런 식으로 저장된다고 치고, 정렬할 또 다른 배열을 만들어서 거기엔
| idx | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| (2, 2) | (4, 1) | (4, 3) | (5, 1) | (6, 3) | (6, 5) |
이렇게 둘 중 큰 수 기준으로 (같으면 순서 상관없이) 정렬하면 만족하는 순서대로 (2, 2) (4, 3) (6, 5) 또는 (6, 3) 을 선택할 수 있으니까, 음 해결 이렇게 생각했다.
근데 이 방식은 다음과 같은 구조를 해결하지 못한다.
(4, 2) (5, 3)
분명 가능한 구조지만 내가 생각한 그리디한 방식으로는 바로 풀 수 없었다. 이게 구분이 불가능한 건 아니지만 큰 수 기준으로 저장하고 바로 정렬 때려서 풀 수 있는 건 아니다...
물론 다른 그리디한 방식으로 풀 수 있겠지만 실제 이 문제를 시간을 주고 풀어라! 하면 이 정도 시도한 것만으로도 실패를 인정하고 정공법을 찾아야만 하는 것 같다.
사실 이 문제는 증가하는 부분 수열 중 가장 길이가 긴 것을 고르는 문제와 똑같다.
길게 적기 싫기도 해서 말로만 설명하면, 최장 증가 부분 수열은 dp를 사용해서 N*N 안에 해결할 수 있다.
dp[i]는 i번째 수를 포함한 증가 부분 수열의 길이
이 점화식 조건 하에 순서대로 저장한다면 만사 OK다.
단지 N = 40000 이기 때문에 이 방법으로는 1억을 거뜬히 넘어간다.
따라서 Nlog N 방법을 찾을 수 밖에 없었다.
dp 방식을 사용할 때 조건으로는 i번째 수보다 작은 수 중 가장 길이가 긴 놈을 골라서 거기에 1 더하는 식으로 저장한다.
어? 그럼 '특정 수보다 작은 수' 라는 조건을 두고, 최장 길이라는 답을 찾는 이분 탐색을 구성할 수 있다.
length[i]는 제일 긴 증가 부분수열의 길이가 i인 가장 작은 숫자
라는 조건 하에 i에 대해서 이분 탐색을 수행하면서 저장하고, 마지막에 length의 길이를 보면 답을 알 수 있을 것이다.
코드 구현
import sys
input = sys.stdin.readline
answer = 0
N = int(input())
l = list(map(int, input().split()))
length = [0]
for i in l:
bot, top = 0, len(length)-1
while bot <= top:
mid = (bot + top) // 2
if i < length[mid]:
top = mid - 1
else:
bot = mid + 1
if top + 1 >= len(length):
length.append(i)
length[top+1] = min(length[top+1], i)
print(len(length)-1)느낀점
잠시 풀다가 처음 생각한 방식으로 틀리고, '음 오늘은 포기할까' 했는데 오늘 포기하면 나중에도 안 할거 같아서 풀고 잔다.
