정의
다익스트라 알고리즘은 양의 가중치를 갖는다는 전제하에
어떤 정점을 기준으로 각 정점에 대한 최단 거리를 구하는 알고리즘이다.
벨만포드는 다익스트라로 해결하지 못하는 문제인 음의 가중치를 갖는 경우에 사용하는 알고리즘이다.
왜 다익스트라로 해결하지 못할까
만약에 1에서 출발한다고 가정할 때
1과 연결된 노드가 2와 3이라고 하자
1과 2 사이의 가중치는 4
1과 3 사이의 가중치는 5라고 할 때
우리는 1과 2 사이의 가중치 4를 최단거리라고 확정한다.
왜냐하면 1에서 2로 가는 다른 방법은 결국 1->3->...->2 일텐데
저 방법은 4보다는 클 것이다.
하지만 그 사이에 음의 가중치가 있다면 우리는 1과 2 사이의 가중치가 4라는 것을 확정짓지 못한다.(1->3->여기 사이가 -100이라면..->2)
따라서 음의 가중치가 있는 경우는 다익스트라로 풀지 못한다.
접근
이 벨만포드의 경우에는 한가지 문제가 있는데 최단거리를 구하지 못할 수도 있다.
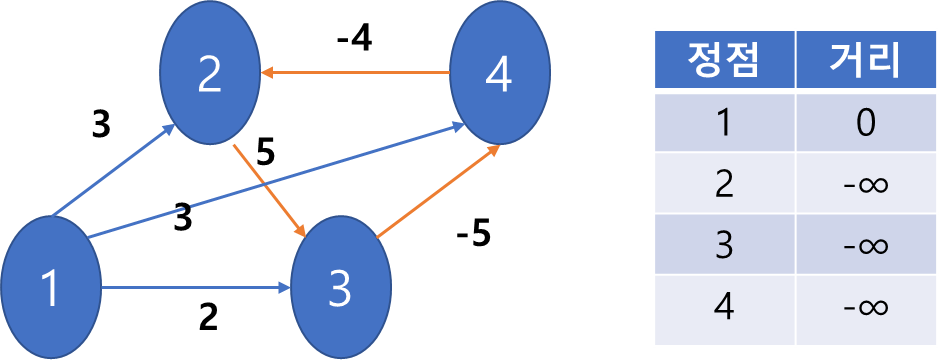
왜냐하면 "음의 사이클"이 존재하는 경우 모든 정점에 대한 최단 거리는 음의 무한대이다.
그림을 보자
저 주황색 간선들을 지나게 한다면 1에서 어떤 정점 노드까지의 거리는 음의 무한대이다.
따라서 최단 거리를 구할 수 없다.
이걸 어떻게 구현해야 할까?
1에서 각 노드들에 대한 최단 거리를 구한다고 가정하자. 음의 가중치가 있기 때문에 다익스트라가 아닌 벨만포드를 이용하도록 한다.
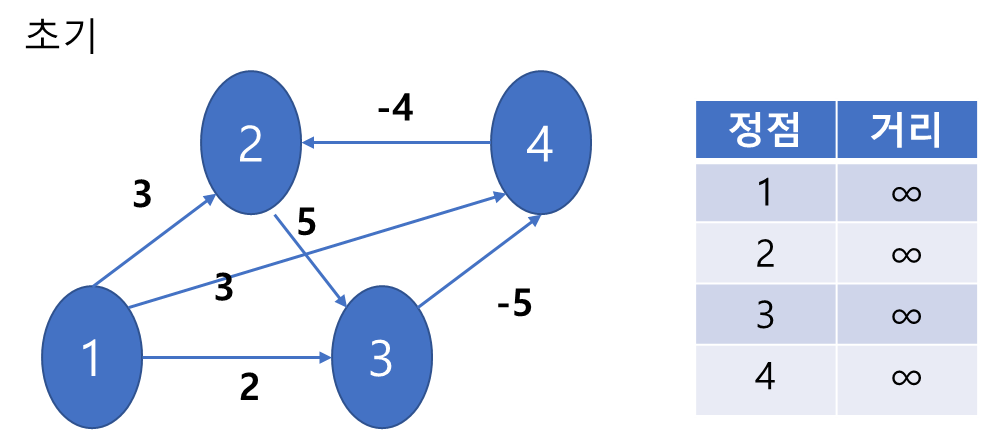
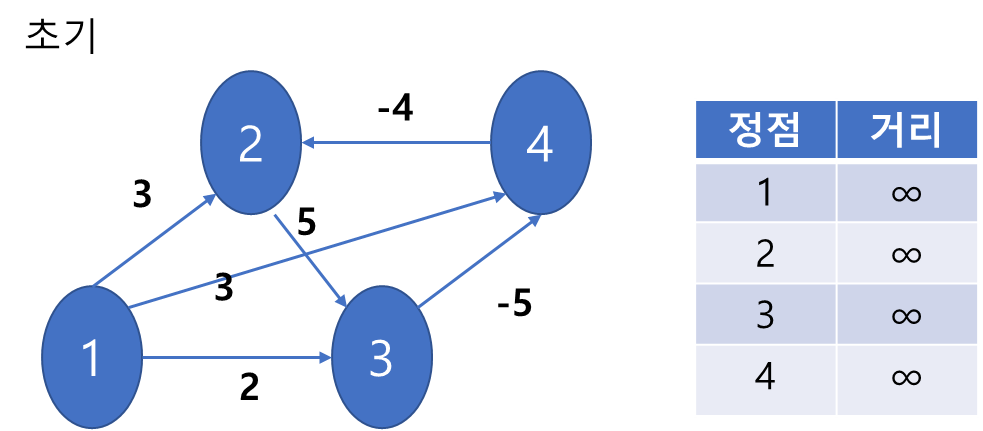
1) 위와 같이 초기화를 진행한다.
최단 경로를 구하기 때문에 처음에는 모든 거리를 무한으로 설정한다.
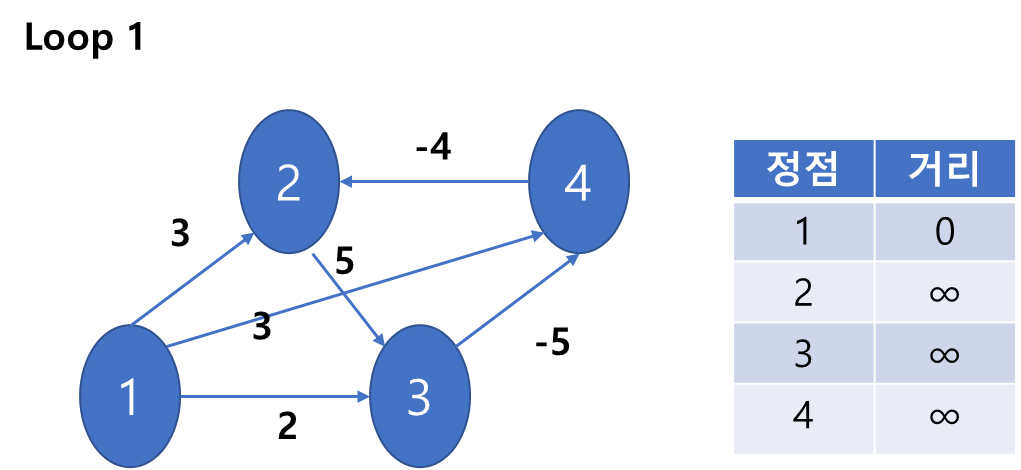
2) 자 이제 하나의 루프를 돌것이다. 출발하는 1번 노드부터 각각의 노드를 들려서 최단 거리를 계산한다. 즉 노드가 N개라고 했을 때 N-1번 이 과정을 반복한다. (이 루프의 과정을 몇번이나 반복할까의 의문은 뒤에서 해결된다) 1에서 시작하고 어떤 곳도 이동하지 않았으므로 1의 거리는 0이다.
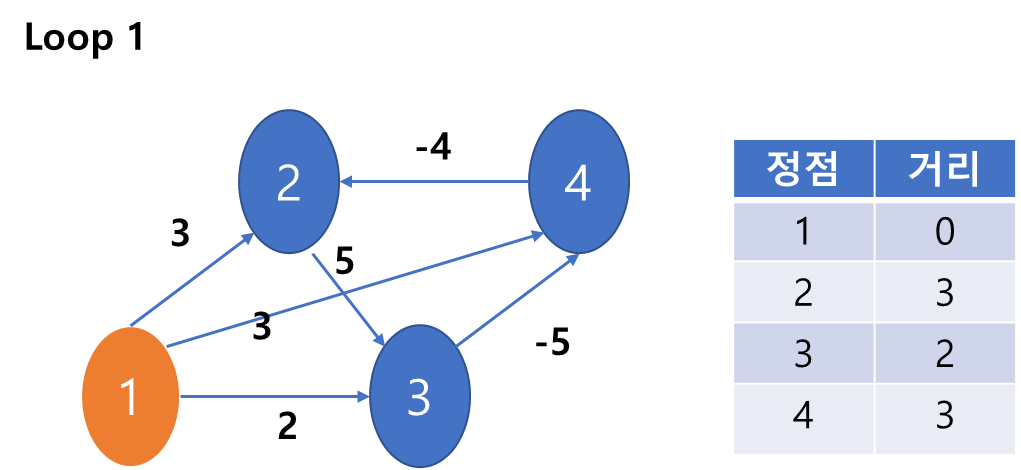
3) 1과 연결된 2와 3,4로 간다.
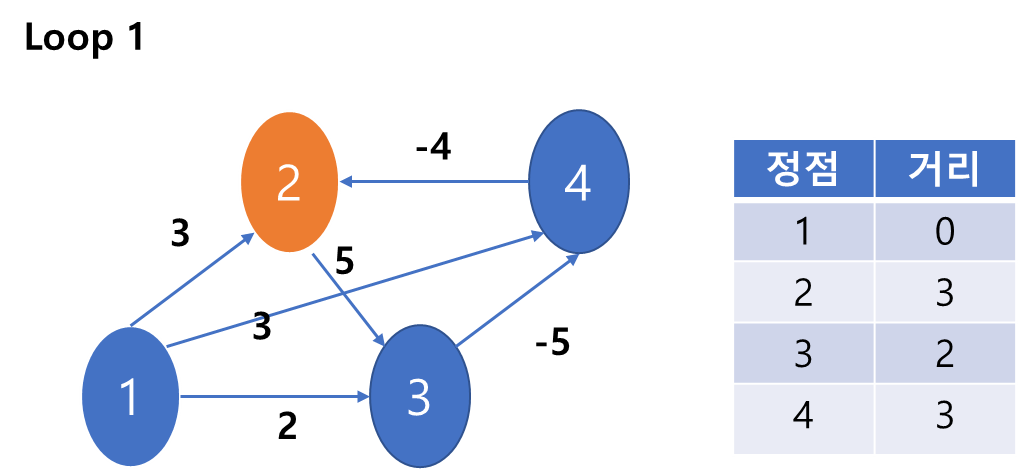
4) 이제 2번 노드를 본다. 2번과 연결된 3번 노드를 보자 1->2->3으로 가는 것보다는 1->3으
로 가는 길이가 더 짧아서 값을 바꾸지 않고 그대로 간다.
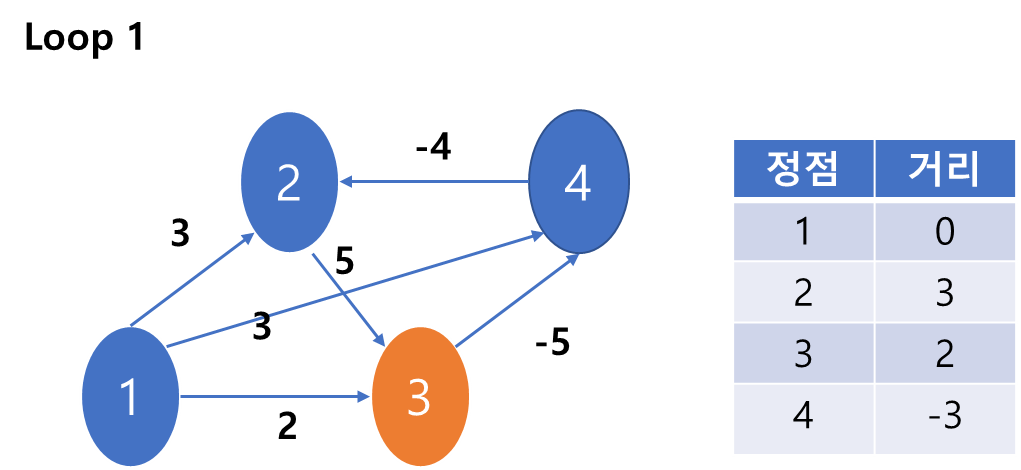
5) 이제 3번 노드를 본다.
1->4으로 가는 것보다 1->3->4로 가는 것이 더 짧기 때문에 갱신이 일어났다.
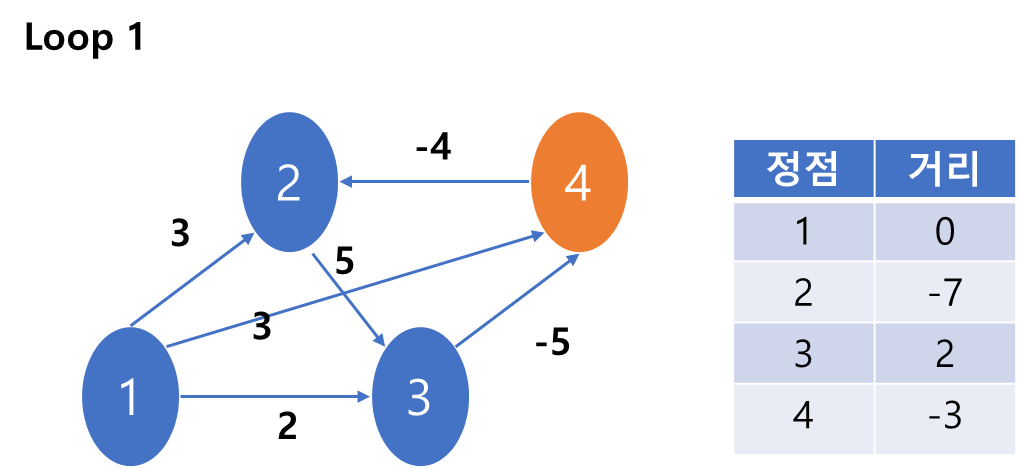
6) 4번 노드를 본다.
4와 연결된 2를 보면 1->2보다 1->3->4->2가 더 짧기 때문에 갱신이 일어났다.
이게 한번의 루프를 돈 것이다.
한번 더 위 과정을 반복하는데 그 이유는 음의 사이클이 존재하는지 보기 위함이다.
한번 더 했을 때 값의 갱신이 일어난다면 그건 모든 값이 결국은 음의 사이클로 인해서 계속 음의 무한대로 간다는 것이다.
따라서 한번의 루프를 더 반복해보자
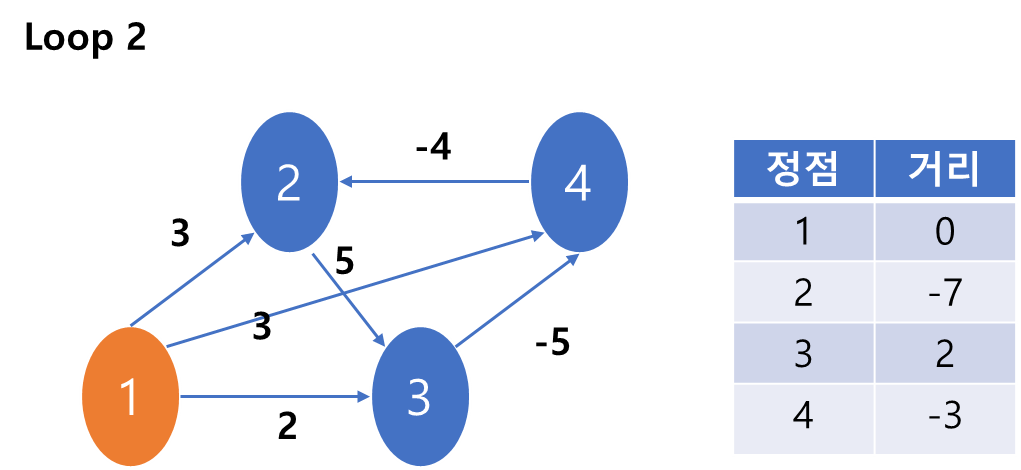
1)1부터 시작하지만 이미 있는 거리가 최소이기 때문에 아무일도 일어나지 않는다.
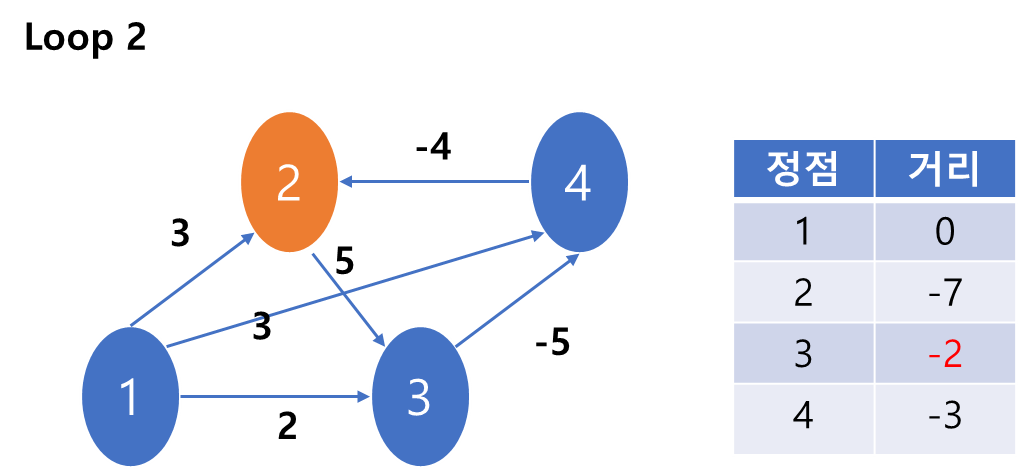
2)2번 노드와 연결된 3번 노드의 거리가 갱신되었다.
결국 1->3 보다는 1->3->4->2->3의 경로가 더 최소였다는 것이다.
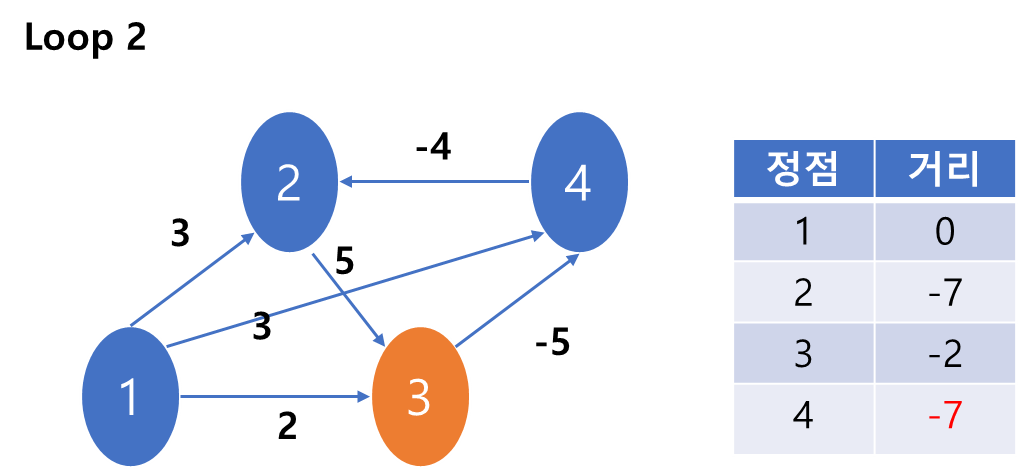
3)3번 노드를 본다. 3번 노드와 연결된 4번 노드의 거리에 갱신이 일어났다.
결국 1->3->4보다는 1->3->4->2->3->4의 경로가 더 최소였다는 것이다.
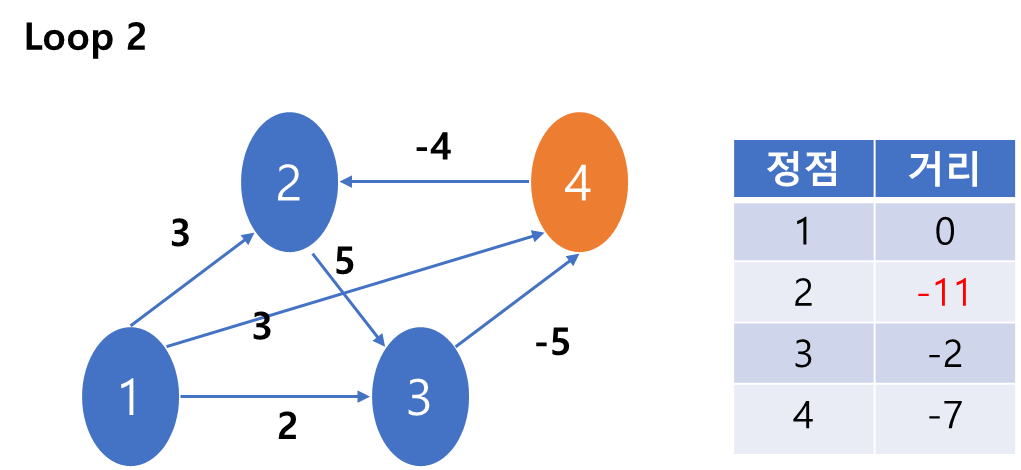
4) 4번 노드를 본다. 4번 노드와 연결된 2번 노드의 거리에 갱신이 일어났다.
결국 1->3->4->2보다는 1->3->4->2->3->4->2의 경로가 더 최소였다는 것이다.
여기서 우리는 두가지를 이해할 수 있다.
하나, 루프를 한번 더 돈다는 것은 최초 한번의 루프를 통해 저장된 경로에 더 최소의 방법이 있는가를 결정하는 것이다.
위의 예시를 보면 최초 한번의 루프에서 2까지의 최소 경로는 1->3->4->2였다.
이 경로가 저장된 2번 노드가 있었다. 다음 루프에서 2번 노드와 연결된 3번 노드를 살펴본다는 것은 1->3->4->2->3을 가는 것이 더 최소인가를 생각해 보는 것이다.
둘, 결국 두번째 루프에서 값의 갱신이 일어난다는 것은 더 최소의 경로가 있다는 것인데 다 갱신된 경로에는 음의 사이클이 들어가 있다.
1->3->4->2->3
1->3->4->2->3->4
1->3->4->2->3->4->2
정리
따라서 음의 사이클이 존재하는 경우에는 최소의 경로는 구하지 못하며 음의 사이클이 있는가를 확인하는 방법은 N개의 노드가 있다고 가정할 때 (1부터 시작하는 각각의 최단 경로를 알아본다고 가정) 결국 2~N까지 N-1번 까지의 노드를 살펴보며 최단 경로를 알아보고 여기서 한번 더 2~N까지 N~1번 까지의 노드를 살펴보며 값의 갱신이 일어나는지 확인하는 것이다.
벨만포드는 위와 같은 문제를 해결해주는데 대신 다익스트라보다 효율적이지 못하다.
왜냐하면 모든 정점을 들려서 최단 거리를 판단하고
그 방법은 한번 더해서 값의 갱신이 일어나는지 확인하기 때문이다.(이유는 음의 사이클의 존재 여부를 확인하기 위해서)
다익스트라는 출발 노드에서 연결된 노드 중에서 최단 거리를 확정하고 그 최단거리가 발생한 그 노드에서 다시 위 과정을 반복한다.
하지만 밸만 포드는 1부터 N까지 다 한다. 모든 노드의 모든 간선을 확인하기 때문에 O(N*E)가 발생한다.
자바 코드
코드는 백준의 웜홀 문제를 풀이한 것입니다.
import java.util.*;
import java.io.*;
public class Main{
static ArrayList<ArrayList<Cost>> road;
static int INF = Integer.MAX_VALUE;
static class Cost{
int v;
int cost;
public Cost(int v, int cost){
this.v =v;
this.cost =cost;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int TC = Integer.parseInt(br.readLine());
StringTokenizer st = null;
while(TC-->0){
st = new StringTokenizer(br.readLine()," ");
int N = Integer.parseInt(st.nextToken());//지점의 수 1~500
int M= Integer.parseInt(st.nextToken()); // 도로의 수 1~2500
int W = Integer.parseInt(st.nextToken()); // 웜홀의 수 1~200
road = new ArrayList<>();
for(int i=0;i<=N;i++){
road.add(new ArrayList<Cost>());
}
for(int i=0;i<M;i++){
st=new StringTokenizer(br.readLine()," ");
int v1 = Integer.parseInt(st.nextToken());
int v2 = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
road.get(v1).add(new Cost(v2,cost));
road.get(v2).add(new Cost(v1,cost));
}
for(int i=0;i<W;i++){
st = new StringTokenizer(br.readLine()," ");
int v1 = Integer.parseInt(st.nextToken());
int v2 = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
road.get(v1).add(new Cost(v2,-cost));
}
int[] pod = new int[N+1];
boolean cycle = false;
for(int i=1;i<=N;i++) {
Arrays.fill(pod,INF);
if (time_Hole(pod, N, i)) {
bw.write("YES");
cycle=true;
break;
}
}
if(cycle==false) bw.write("NO");
bw.write("\n");
}
bw.flush();
bw.close();
br.close();
}
static boolean time_Hole(int[] pod,int N,int start){
pod[start]=0;
boolean update = false;
//최대 N-1번 예를 들어 start가 N번이고 각각의 정점이 하나의 노드와 연결된 경우
for(int i=1;i<N;i++) {
update= false;
//처음 pod[start]=0부터 점차 초기화 하는 과정
for (int j = 1; j <= N; j++) {
for (Cost x : road.get(j)) {
if (pod[j]!=INF && pod[x.v]>x.cost+pod[j]){
pod[x.v]=x.cost+pod[j];
// 민약 i가 N-1 때까지 갱신이 일어난다면
// 1. 음의 가중치가 있다.
// 2. start가 N이었다!
update= true;
}
}
}
// 더 이상 update가 일어나지 않는다 = 다 양의 가중치
if(!update) break;
}
//마지막 N-1번까지 update가 일어났다는 것은 음의 가중치가 있을지도 모른다는 가정이 발생
// 보통 다익스트라는 마지막에 갱신이 일어나지 않음 거기서 끝
if(update){
for(int i=1;i<=N;i++){
for(Cost x : road.get(i)){
//따라서 한번더 업데이트가 발생했으니 음의 사이클이 있다 true
if(pod[x.v]!=INF && pod[x.v]>x.cost+pod[i]){
return true;
}
}
}
}
return false;
}
}