Universal Approximation

이 포스트는 Youtube "혁펜하임"의 강의를 참고하여 정리한 글임을 밝힙니다.

universal approximation 이란?

"A neural network with one hidden layer can approximate any function $f:R^N\to\R^M$ with arbitrary precision."

1. 개념을 직관적으로 이해하기

미적분 시간에 리만 적분의 idea 를 그림으로 나타낸 것을 본적이 있다.

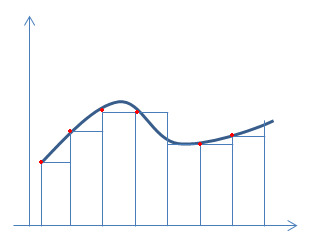
그래프 아래의 면적을 근사하기 위하여 주어진 함수의 구간을 여러개의 아주 작은 직사각형(깍두기!) 으로 나누어, 이를 무한히 더하는 개념이다.

universal approximation의 개념도 이와 비슷한게, 여러개의 (아주 작은 구간에서 정의된) 함수의 합으로 나타내고자 하는 것이다. 다만 그 대상이 나타내고자 하는 것이 함수 아래의 면적이 아닌 함수 $g$ 이다.

이 아이디어를 기반으로, neural network로 $g$를 나타낼 수 있다는 것이 universal approximation 이다.
다음과 같은 함수 $g$를 표현하고자 한다고 가정하자.

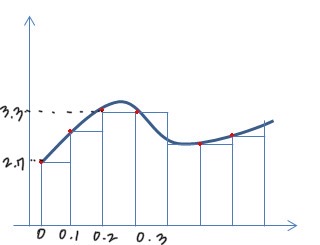
2. Perceptron으로 만들기

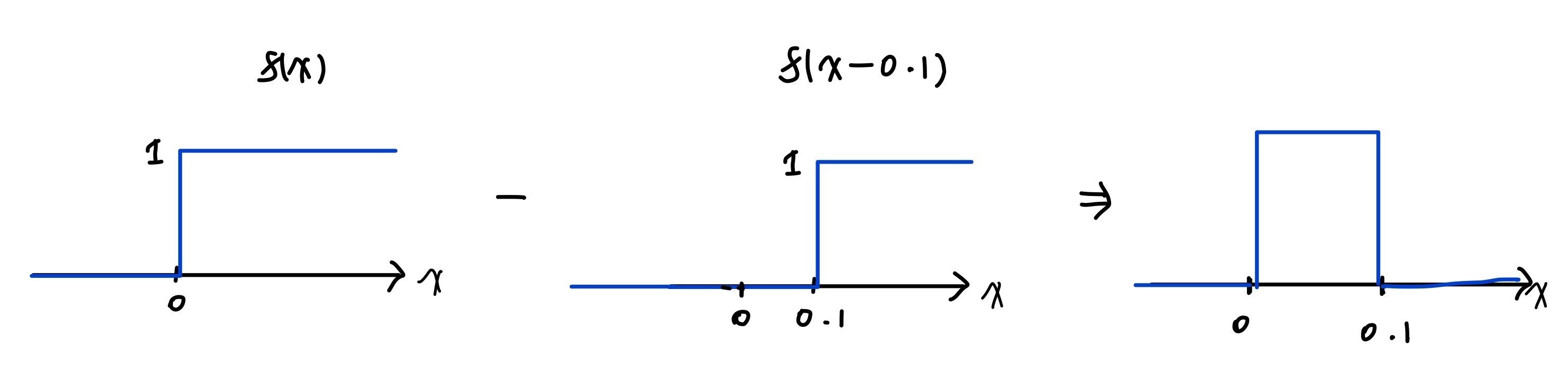
기본적인 perceptron은 왼쪽과 같이 생겼는데, 이를 0.1만큼 평행이동 하여 새로운 perceptron을 만들고, 이를 원래의 perceptron 에서 (-) 하면 [0,0.1] 범위에 '깍두기' 를 만들 수 있다. 이걸 표현하고자 하는 함수에 적용해보자.

• 0과 0.1 구간의 2.7이라는 값은 다음과 같이 표현할 수 있다:
  $2.7(f(x)-f(x-0.1))$

• 0.2와 0.3 구간의 3.3이라는 값은 다음과 같이 표현할 수 있다:
  $3.3(f(x-0.3)-f(x-0.2))$

What if 아주 촘촘하게 깍두기들을 연결하면? -> 함수가 표현 된다!!!

이를 neural net으로 표현해보자.

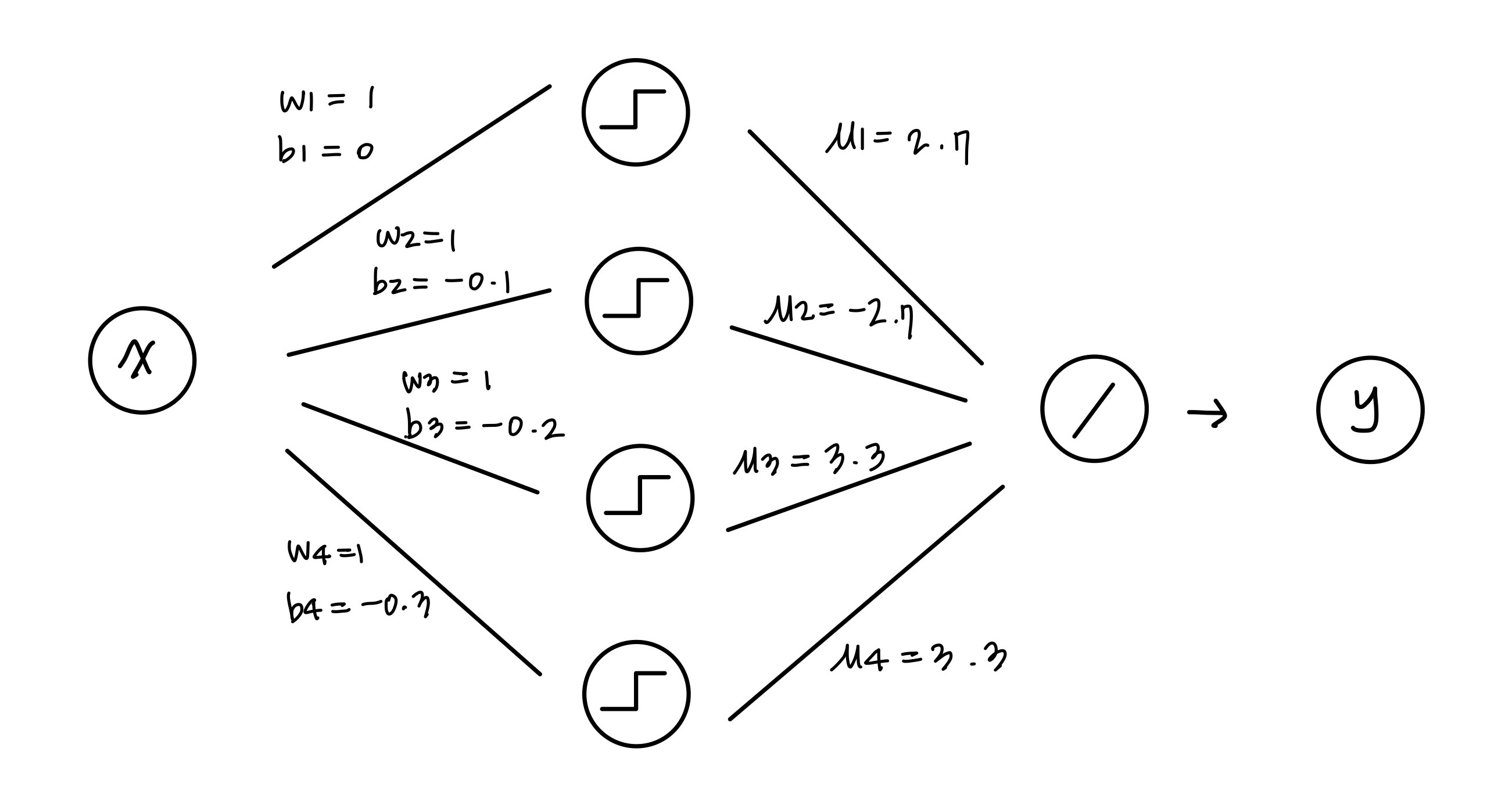
간단한 neural net으로 g를 표현하였다! 실제로 근사의 정확도를 높이기 위해서는 엄청 나게 많은 node 가 필요할 것이다.

3. Sigmoid로 만들기

기본적인 sigmoid를 다음과 같이 변형하면, 거의 perceptron과 유사한 모양이 된다. 따라서 (2)에서와 같은 방법으로 $g$를 근사할 수 있다.

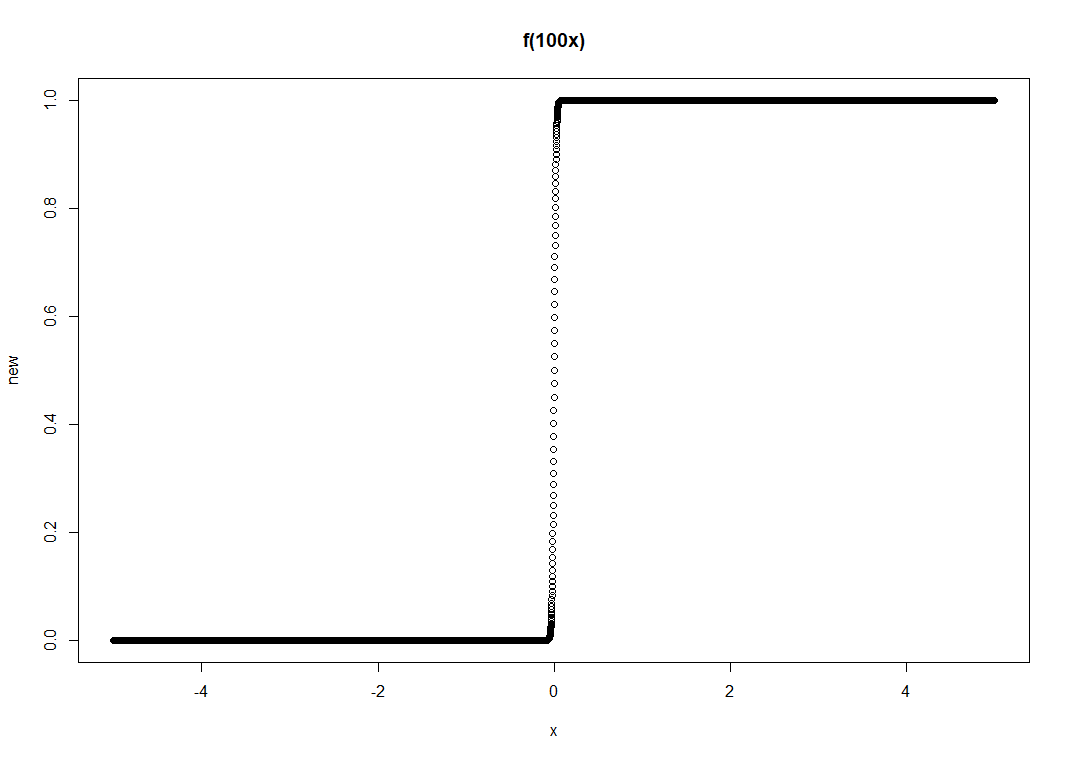
4. ReLU로 만들기

will be updated

[References]

• Youtube "혁펜하임"