요즘 딥러닝을 공부하는데 많은 논문에서 Entropy, Cross Entropy, KL Divergence ... 등이 언급된다. 그래서 이번기회에 확실히 공부해보고자 이 글을 작성한다.

학교 강의인 기계학습의 김휘용 교수님 말씀을 참고하였습니다.

---

정보(Information)

먼저 정보에 대해 언급하고자 한다.

'겨울에 눈이 온다' 와 '여름에 눈이 온다'

두개의 글 중 어떤 것이 정보량이 큰가?

후자의 정보가 정보량이 크다.
'겨울에 눈이 온다' 라는 내용은 당연히 알지만, '여름에 눈이 온다' 라는 내용은 매우 불확실한 정보이다.
그렇기 때문에 후자가 정보량이 크다고 하는 것이다.

즉, Uncertainty(불확실성)가 큰 정보가 정보량이 높은 것이다.

정보량은 사건 $x_i$ 에 대해

$-log_2p(x_i)$

와 같이 계산한다. 비트량으로 나타내기 위하여 log 밑을 2로 사용한다.

예를 들어, '겨울에 눈이 온다' 라는 확률이 ${7 \over 8}$ 이고, '여름에 눈이 온다' 라는 확률이 ${1 \over 8}$ 이라고 한다면,

전자의 전보량은 $-log_2{7 \over 8}$ $\doteqdot$ 0.19, 후자의 정보량은 $-log_2{1 \over 8}$ = 3

즉, 전자는 비교적 확실한 정보이기에 낮은 비트량으로 나타낼 수 있지만, 후자는 불확실한 정보이기에 3 만큼의 비트량으로 나타내야 한다.

---

엔트로피(Entropy)

엔트로피는 평균 정보량을 뜻한다.

일련의 사건들에 대해 얼마만큼의 비트량으로 표현할 수 있는가? 에 대한 답이 될 수있다.

N개의 정보량의 평균 = $-\sum_{i=1}^N p(x_i)log_2p(x_i)$

두가지 예를 들어 보겠다.

1.

4면 주사위 1,2,3,4 는 모두 같은 확률인 ${1 \over 4}$ 을 지닌다.

엔트로피는 -$4*{1 \over 4}log_2{1 \over 4}$ 이므로 2 이다.

즉, 2비트로 4면 주사위를 표현할 수 있는 것이다. '(0,0), (0,1), (1,0), (1,1)'

2.

만약 이상한 4면 주사위 1,2,3,4 가 각각 ${1 \over 2}$, ${1 \over 2}$, 0, 0 의 확률을 가진다고 가정하면

엔트로피는 -${1 \over 2}log_2{1 \over 2}$ + -${1 \over 2}log_2{1 \over 2}$ 이므로 1 이다.

즉, 1비트로 이상한 4면 주사위를 표현할 수 있는 것이다.'(0), (1)'

예시

직관적인 예시를 들어 보겠다.
한국의 대통령 후보 '조 후보', '김 후보' 지지율이 각각 50%, 50% 이다.
미국의 대통령 후보 'James 후보', 'Alex 후보' 지지율이 각각 80%, 20% 이다.
어떤 나라의 엔트로피가 높은 가?

답은 한국이다. 직관적으로도 미국은 누가 대통령이 될 지 명확하지만, 한국은 누가 대통령이 될 지 불확실하다. 불확실성이 큰 한국의 대통령을 뽑는 엔트로피가 높은 것이다.
실제 계산도 마찬가지이다.

한국 대통령 선거 엔트로피: -${1 \over 2}log_2{1 \over 2}$ + -${1 \over 2}log_2{1 \over 2}$ = $2$
미국 대통령 선거 엔트로피: -${8 \over 10}log_2{8 \over 10}$ + -${2 \over 10}log_2{2 \over 10}$ $\doteqdot$ $0.26$ + $0.46$ = $0.72$

🤔참고로 엔트로피가 가장 높을 때는 각각의 확률이 동등할 때 이다.

---

교차 엔트로피(Cross-Entropy)

실제 세계에서 $p(x)$ 의 확률분포를 알기 어렵다.
따라서 우리가 추측 또는 추정한 $q(x)$ 의 확률분포를 이용한다.

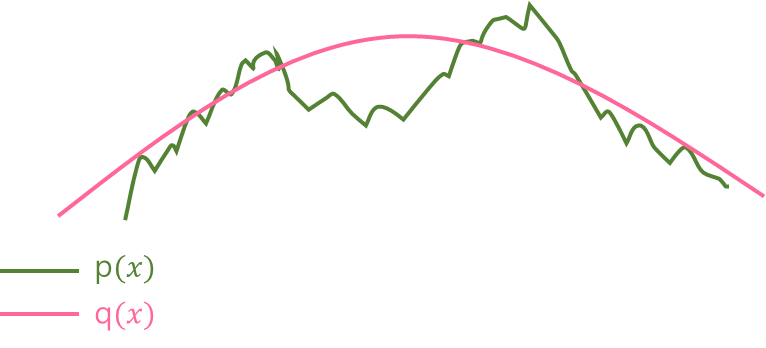
$p(x)$ 가 실제 확률분포이고, $q(x)$ 는 정규분포를 따른다고 가정한 추정분포이다.

따라서 확률분포 $p(x)$ 에 대한 확률분포 $q(x)$ 의 교차 엔트로피를 다음과 같이 계산한다.

N개의 교차 엔트로피 H(p,q) = $-\sum_{i=1}^N p(x_i)log_2q(x_i)$

이진 교차 엔트로피(Binary Cross-Entropy)

만약 실제 값이 $x_1$, $x_2$ 으로 두가지 라면 다음과 같이 계산한다.

H(p,q) = $-p(x_1)log_2(q(x_1))-p(x_2)log_2(q(x_2))$
= $-p(x_1)log_2(q(x_1))-(1-p(x_1))log_2(1-q(x_1))$

🤔Cross-Entropy Loss 에 대해
딥러닝 모델 분류를 할때 보통 정답 값 y 를 (1, 0) 로 사용한다.
$H(x)$ 가 우리가 측정, 계산한 값이라면

$H(y,H(x))$ = $-ylog(H(x))$ $-(1-y)log(1-H(x))$
정답이 1과 0 이므로 결국 남는 것은 $-log(H(x))$ 이고 정보량이 된다.

이 값을 최소화 한다는 건 $q(x)$ 를 $p(x)$ 에 근사화하는 것이다.

KL Divergence(쿨백-라이블러 발산)

두 확률분포 p,q 의 차이를 알기 위해 KL Divergence 를 이용한다.
확률분포 q에서 p로의 KL Divergence(상대 엔트로피) 는 다음과 같이 정의 된다.

$D_{KL}(p||q)$ = $-\sum_{i=1}^N p(x_i)log_2({p(x_i) \over q(x_i)})$ = $H(p,q)$ - $H(p,p)$ $\geqq0$

예시

a, b, c, d, e, f, g 에 대한 정보의 확률이 $p(X)$ 와 그에 따른 '$p(X)$ 의 정보량' 과 계산값인 $q(X)$ 와 그에 따른 '$q(X)$ 의 정보량' 이 다음과 같은 표에 있다.

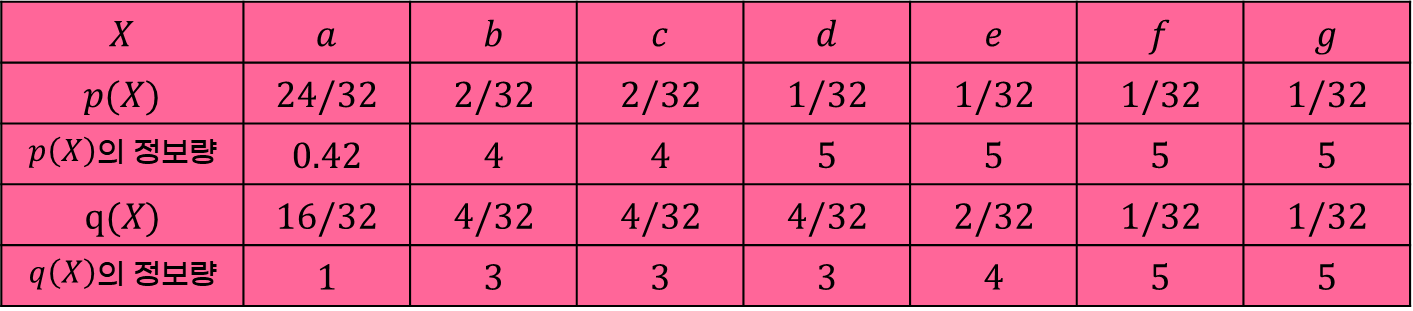
$H(p,p)$ = (24 ÷ 32 × 0.42) + (2 ÷ 32 × 4) + (2 ÷ 32 × 4) + (1 ÷ 32 × 5) + (1 ÷ 32 × 5) + (1 ÷ 32 × 5) + (1 ÷ 32 × 5) = 1.44

$H(p,q)$ = (24 ÷ 32 × 1) + (2 ÷ 32 × 3) + (2 ÷ 32 × 3) + (1 ÷ 32 × 3) + (1 ÷ 32 × 4) + (1 ÷ 32 × 5) + (1 ÷ 32 × 5) $\doteqdot$ 1.66

$D_{KL}(p||q)$ = $H(p,q)$ - $H(p,p)$ $\doteqdot$ $1.66 - 1.44$ = 1.22

즉 위 값을 줄이는 방식으로 q 를 잘 조정할 것이다.

🤔이진 값이라면?
딥러닝 모델 분류할 때 정답 값인 1과 0 을 쓴다.
이와 같은 이진분류라면 $p(x)$ = 1 또는 0 이므로 $H(p,p)$ = 0 이 되므로 $H(p,q)$ 만 남는다.
즉, 이진 교차 엔트로피가 되는 것이다.

---

결국 정보량, 크로스 엔트로피, KL Divergence 모두 딥러닝 분류를 할때 비슷하게 쓰일 수 밖에 없는 개념인 듯하다.
다음엔 이어서 관련있는 Softmax 부터 글을 써보려고 한다.

부족한 점이 많은 글일 수 있으므로 따뜻한 지적 부탁드립니다😍