백트래킹 알고리즘 정리

백트래킹은 기본적으로 DFS 알고리즘을 기반으로 해서 탐색을 진행하다가, 해당 노드가 조건에 맞지 않는다면 더이상 탐색하지 않는다.

1. 진행중인 경로가 해답을 찾을 가능성이 있는 경우 유망함
2. 진행중인 경로가 답을 찾을 가능성이 없다면 유망하지않음
3. 유망하지 않은 트리를 더이상 탐색하지 않으며 가지치기

이렇게 총 3가지로 나눠볼수 있다.

이는 DFS알고리즘과 헷갈릴수 있는 부분인데, DFS는 완전 탐색을 목적으로 하며 깊이 우선으로 탐색하고 이를 재귀함수로 구현한다.

백트래킹도 재귀 함수를 이용해서 구현을 하는것이 일반적이지만, 조건을 비교해보고 해당 조건에 더 알맞은 노드로 이동한다.

대표적인 문제가 N-Queen 문제이다.

즉 체스에서 가로, 세로, 대각선의 공격이 가능한 Queen을 N x N 만큼의 체스판에서 N개의 Queen이 서로 공격할수 없도록 하는 경우의 수를 구해야하는 것인데,

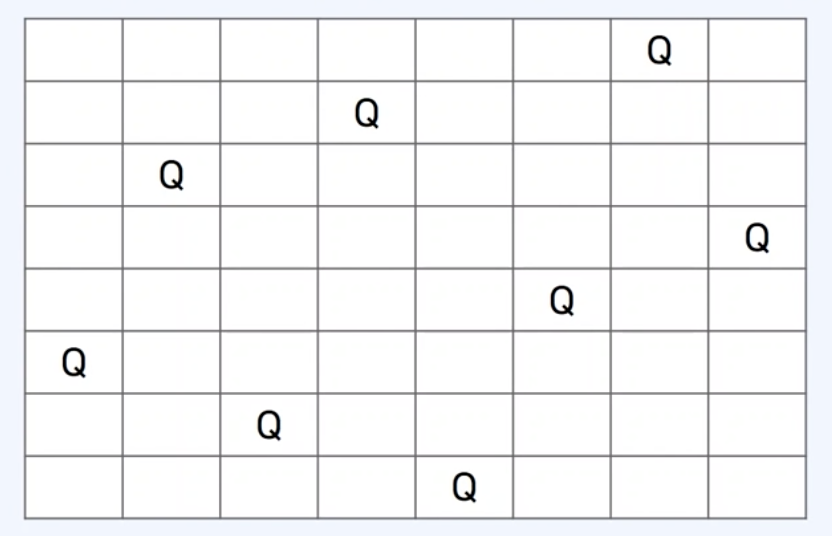
예를들어서 N이 8이라고 했을때, Queen을 이런식으로 놓는다면 서로 공격을 못하게 되기때문에, 이런 경우의수의 총합을 구하는 것이다.

만약 이를 완전탐색으로 구현한다고 치면, 굉장히 복잡해지고 시간복잡도도 굉장히 높아진다.

하지만 백트래킹을 이용해서 가능해보이는 경우의수만 실행하도록 한다면 효율적으로 접근할수 있다.

만약에 첫번째 퀸을 [0,6] 에 두었디고 생각해보자.

그 다음 퀸은 첫번째 퀸의 대각선, 세로에 놓아지면 안되므로 이부분은 제거해야한다.

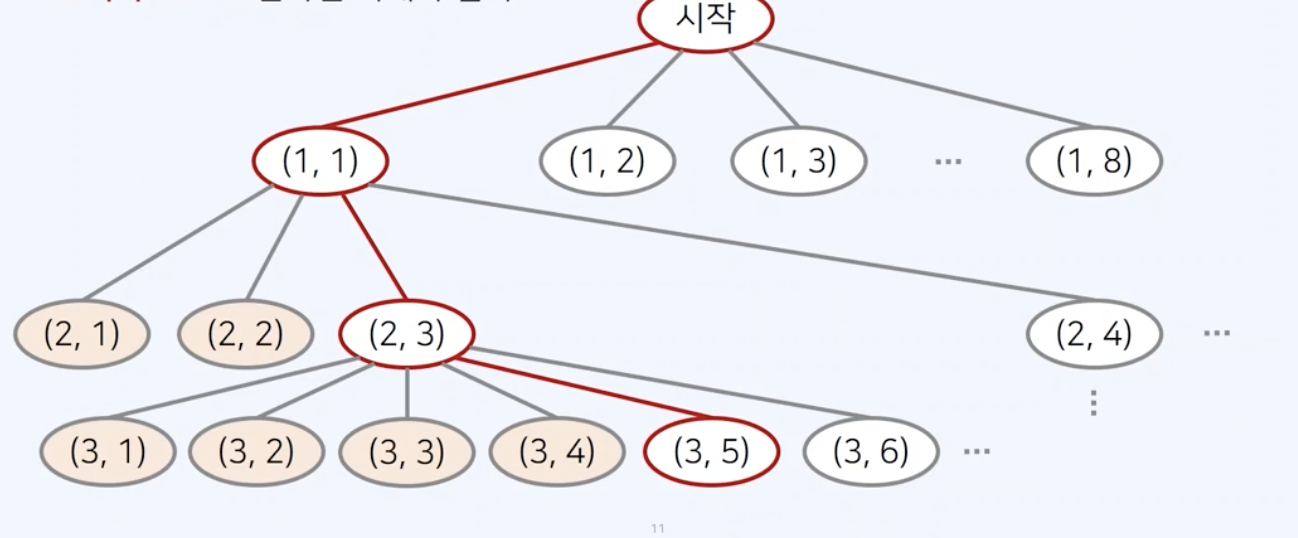
이를 이제 트리구조로 나타낸다면 이렇게 된다.

1행 1열에 첫번째 퀸이 놓아졌다면 후에 2행 1열, 2행 2열엔 퀸이 놓아질수 없으므로 2행 3열에 퀸이 놓아지고,

또 3행 5열에 퀸이 놓아지는 것이다.

function 재귀함수(){
  if(종료조건을 만족한다면){
    처리
  }

  for 자식 노드들을 하나씩 확인해보며{
    if 임의 조건을 충족한다면{
      1. 자식 노드 방문 처리
      2. 재귀 함수 호출
      3. 자식 노드 방문 처리 해제
    }
  }
}

백트래킹의 재귀함수는 보통 이런식의 흐름으로 진행된다.

const input = `8`;

const N = Number(input);

let queens = [];

let count = 0;

function possible(x, y) {
  for (let arr of queens) {
    const [a, b] = arr;

    // 만약 퀸이 놓여진 자리에 가로 세로가 같다면
    if (a === x || b === y) {
      return false;
    }

    // 퀸이 놓여진 자리의 기울기가 서로 같다면 
    if (Math.abs(a - x) === Math.abs(b - y)) {
      return false;
    }
  }

  return true;
}

function dfs(row) {
  if (row === N) {
    count += 1;
  }

  for (let i = 0; i < N; i++) {
    if (!possible(row, i)) {
      continue;
    }

    queens.push([row, i]);
    dfs(row + 1);
    queens.pop();
  }
}

dfs(0);

console.log(count);

위의 방식을 따라서 N-Queen 문제를 처리한 것이다.