📙 Risk-Parity?

비중은 다르게, 위험 기여도는 동일하게!

Risk-Parity 투자 전략은 Bridgewater Associates의 Ray Dalio All-weather portfolio 투자 전략으로도 유명하다. 본 투자 전략은 이름 그대로, 포트폴리오에 속한 종목들의 포트폴리오 위험($\sigma_p$) 기여도($RC$: Risk Contribution)가 동일해지도록 자산을 배분하는 전략이다.

Risk-Parity 투자 전략은 상관계수($\rho$)가 낮은 자산들을 기반으로 운용되는 포트폴리오에서 효과적이다. 가장 단순한 예로, 주식과 채권 - 2가지 자산으로 운용되는 포트폴리오를 고려해보자. 우리는 코스툴라니의 달걀(Kostolany's egg) 모형을 통해 금리의 움직임에 따른 주식과 채권의 대비되는 수익 구조를 확인할 수 있다.

만일, 금리의 급격한 상승으로 주식 매도율이 증가했고, 이에 따라 주식의 변동성이 높아졌다고 가정해보자. 이 경우, 주식의 $\sigma$는 자연히 채권에 비해 상승할 것이고, 포트폴리오 내 주식과 채권의 각 $\sigma$는 비대칭적 구조를 보일 것이다.

Risk-Parity 투자 전략은 위의 상황에서 힘을 발휘한다. 본 투자 전략은 주식의 $\sigma$ 비중이 채권에 비해 상대적으로 높아짐에 따라 포트폴리오 내 주식 보유 비중을 낮추고, 반대로 채권 보유 비중을 높임으로써 두 자산의 $\sigma$가 동일해지도록 한다. 즉, 특정 종목의 하락세를 방어 및 보완하여 안정적인 상승세를 꾸려가는 투자 전략인 셈이다.

📙 General concept

0. Total risk

시장 내 $N$개의 자산을 각각 $w_i$($i=1$ ~ $N$)의 비중으로 내포하는 포트폴리오 $p$가 존재한다고 가정하자. 그리고, 포트폴리오 $p$의 총 위험 $TR_p$를 $\sigma_p^2$이라고 하겠다.

$\sigma_p^2$은 다음의 산식으로 계산될 수 있다:

$TR_p = \sigma_p^2 = \sum_{i=1}^N \sum_{j=1}^N w_i w_j \sigma_{ij}$

1. Marginal risk contribution

다음으로, 포트폴리오 $p$에 속한 자산 $i$의 한계위험 기여도($MRC_i$, Marginal Risk Contribution of asset $i$ in portfolio $p$)를 살펴보겠다. $MRC_i$는 포트폴리오 $p$에 속한 개별 자산 $i$의 비중($w_i$) 한 단위 증가에 따른 전체 포트폴리오 $p$의 총 위험 $TR_p$의 변화량이다.

$MRC_i$는 다음의 편미분 산식으로 계산된다:

$MRC_i = \frac{\partial \sigma_p^2}{\partial w_i}$

일례로, 포트폴리오 $p$에 두 개의 자산 $1,2$만 존재한다고 가정하자. 이 경우, $TR_p$는 다음의 산식으로 계산할 수 있겠다:

$TR_p = \sigma_p^2 = w_1^2\sigma_1^2 + w_2^2\sigma_2^2 + 2w_1w_2\sigma_{1,2}$

더 나아가, 두 자산의 $MRC$는 다음의 산식으로 계산된다:

$MRC_1 = \frac{\partial \sigma_p^2}{\partial w_1} = 2w_1\sigma_1^2 + 2w_2\sigma_{1,2}$

$MRC_2 = \frac{\partial \sigma_p^2}{\partial w_2} = 2w_1\sigma_2^2 + 2w_1\sigma_{1,2}$

2. Risk contribution

지금까지 포트폴리오 $p$에 속한 개별자산 $i$의 한 단위 증가에 따른 위험 기여도의 증가량을 확인하였다. 다음으로, 개별자산 $i$가 포트폴리오 $p$의 위험에 기여하는 정도($RC_i$, Risk Contribution of asset $i$ in portfolio $p$)를 살펴보겠다.

$RC_i$는 다음의 산식으로 계산된다:

$RC_i = w_i MRC_i$

즉, $RC_i$는 개별자산 $i$의 비중과 $MRC_i$의 곱으로 이루어짐을 알 수 있다.

정리하자면, 상단의 과정을 통해 포트폴리오 $p$에 속한 개별자산 $i$의 $MRC_i$와 $RC_i$를 파악할 수 있었다.

마지막으로, $RC_i$를 통해 $TR_p$를 새로이 정의할 수 있다. 각 개별자산 $i$가 포트폴리오 $p$에 기여하는 위험의 합은 곧 총위험 $TR_p$라고 할 수 있으며, 이에 따라 $TR_p$는 다음의 산식으로 재정의될 수 있다:

$TR_p = \sigma_p^2 = \sum_{i=1}^N RC_i$

🚫 Cautions

상단의 과정을 통해 $TR_p$를 $RC_i$의 합으로 정의할 수 있었다. 그러나, 산식 내 각 $RC_i$를 분해할 경우, 상단의 식에 모순이 있음을 알 수 있다.

앞서 예제처럼 두 개의 자산만으로 포트폴리오 $p$가 구성되었다고 가정하자. 이 경우, $TR_p$는 다음의 산식으로 계산될 것이다:

$TR_p = \sigma_p^2 = \sum_{i=1}^2 RC_i$

또한, 개별자산 $i=1,2$의 $RC_i$는 다음과 같이 계산된다:

$RC_1 = w_1 MRC_1 = 2w_1^2 \sigma_1^2 + 2w_1w_2\sigma_{1,2}$

$RC_2 = w_2 MRC_2 = 2w_2^2 \sigma_2^2 + 2w_1w_2\sigma_{1,2}$

이후, $TR_p$는 다음의 산식으로 새로이 정의할 수 있다:

$TR_p = RC_1 + RC_2 = 2(w_1^2\sigma_1^2 + w_2^2\sigma_2^2 + 2w_1w_2\sigma_{1,2}) = 2\sigma_p^2 \\ TR_p = \sigma_p^2 \neq 2\sigma_p^2$

즉, $TR_p = \sum_{i=1}^N RC_i$는 항상 성립하지 않는 성질임을 알 수 있다.

해당 성질을 고려해 $TR_p$를 분산 $\sigma_p^2$ 대신 표준편차 $\sigma_p$로 대체한다. 이는 표준편차의 Degree of 1 성질을 활용한 것으로, 상단의 문제점을 해결하기에 용이하다.

이를 바탕으로, $TR_p = \sigma_p$라고 설정한다면, $MRC_i$와 $RC_i$는 다음과 같이 재정의될 수 있겠다:

$MRC_i = \frac{\partial \sigma_p}{\partial w_i},~RC_i = w_i MRC_i$

향후의 포스트 전개는 $TR_p = \sigma_p$로 진행하겠다.

3. Risk-Parity

Risk-Parity 투자 전략의 핵심은 포트폴리오 $p$에 속한 모든 개별자산이 포트폴리오 $p$의 총 위험 $\sigma_p$에 동일하게 기여하도록 설계하는 것이다. 포트폴리오 $p$에 $N$개의 자산이 있다고 가정할 때, 위의 설명은 다음의 산식으로 표현될 수 있겠다:

$RC_i = \frac{TR_p}{N}$

정리하자면, 개별자산들의 비중을 유기적으로 조정하며 각 자산별 포트폴리오 $p$에 기여하는 위험이 동일해지도록 운용하는 투자 전략을 Risk-Parity라고 한다.

📙 Risk-Parity with two assets

상단에서 배운 Risk-Parity 투자 전략을 두 개의 자산으로 구현해보자. 우선, 포트폴리오 $p$의 수익률은 $r_p$, 총 위험은 $TR_p = \sigma_p$이다. 또한, 각 자산 $1,2$의 수익률은 $r_1, r_2$, 비중은 $w_1, w_2$, 그리고 위험은 $\sigma_1, \sigma_2$이다.

먼저, $r_p$를 자산 $1,2$로 전개해보자:

$r_p = w_1r_1 + w_2r_2 \\ w_1 + w_2 = 1 ~\cdots ~(1st)$

다음으로, $TR_p$를 자산 $1,2$로 전개해보자:

$TR_p = \sigma_p = \sqrt{w_1^2\sigma_1^2 + w_2^2\sigma_2^2 + 2w_1w_2\sigma_{1,2}}$

위의 산식을 바탕으로 $MRC_1, MRC_2$를 계산하겠다:

$MRC_1 = \frac{\partial\sigma_p}{\partial w_1} = \frac{w_1\sigma_1^2 + w_2\sigma_{1,2}}{\sigma_p} \\ MRC_2 = \frac{\partial\sigma_p}{\partial w_2} = \frac{w_2\sigma_2^2 + w_1\sigma_{1,2}}{\sigma_p}$

이후, 계산된 $MRC_1, MRC_2$를 통해 $RC_1, RC_2$를 계산할 수 있다:

$RC_1 = w_1 MRC_1 = \frac{w_1^2 \sigma_1^2 + w_1w_2\sigma_{1,2}}{\sigma_p} \\ RC_2 = w_2 MRC_2 = \frac{w_2^2 \sigma_2^2 + w_1w_2\sigma_{1,2}}{\sigma_p}$

상단의 <3. Risk-Parity>에 따르면, Risk-Parity 투자 전략 내에서는 모든 개별자산의 위험 기여도가 동일해야 한다. 이는 다음의 산식으로 표현할 수 있다:

$RC_1 = RC_2 = \frac{\sigma_p}{2}$

해당 산식에 상단의 $RC_1, RC_2$을 대입하여 풀이한다면 다음의 식이 도출된다:

$w_1\sigma_1 = w_2\sigma_2 ~\cdots ~(2nd)$

마지막으로, 위의 수식 중 $(1st)$와 $(2nd)$를 통해 $w_1, w_2$를 계산하겠다:

$w_1 + w_2 = 1 ~\cdots ~(1st) \\ w_1 \sigma_1 = w_2 \sigma_2 ~\cdots ~(2nd) \\ \vdots \\ w_1 = \frac{\sigma_2}{\sigma_1 + \sigma_2}, ~w_2 = \frac{\sigma_1}{\sigma_1 + \sigma_2}$

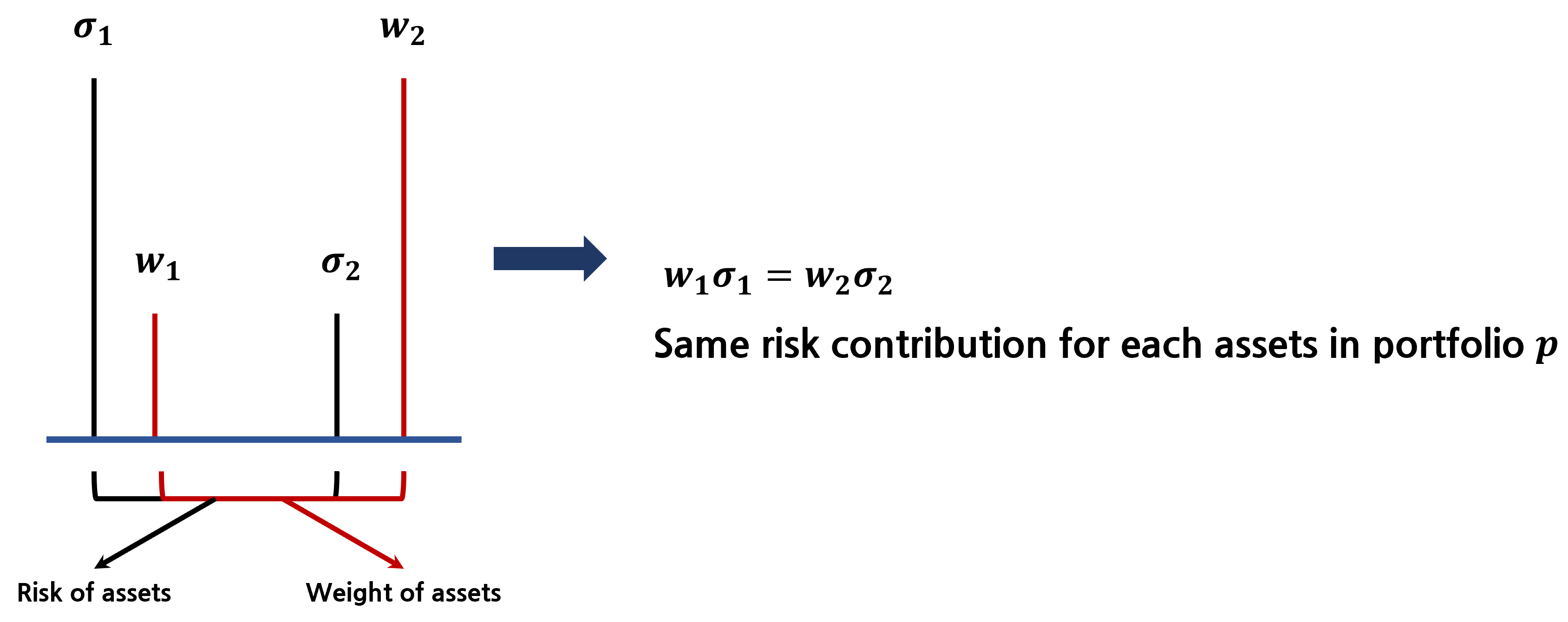
즉, 두 개의 자산 $1,2$를 활용한 Risk-Parity 투자 전략은 각 자산이 $w_1 = \frac{\sigma_2}{\sigma_1 + \sigma_2}, ~w_2 = \frac{\sigma_1}{\sigma_1 + \sigma_2}$의 비중으로 조정 및 투자가 이루어지는 전략이라고 할 수 있겠다.

상단의 과정을 그림으로 간단히 표기하면 다음과 같다:

📙 Code explanation

주식과 채권, 두 개의 자산을 활용한 Risk-Parity 투자 전략을 Python 코드로 구현하였다.

0. Libraries

# Essential libraries

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import gridspec

1. Data

본 투자 전략에서 활용된 자산은 TQQQ와 TMF로, 각각 S&P500 지수와 미국 20년 장기국채 지수를 추종하는 3X leverage ETF 상품이다. 해당 자산을 선정한 이유는 다음과 같다:

1. 코스툴라니의 달걀에 의하면, 주식과 채권은 금리의 움직임에 따라 서로 상반되는 수익구조를 보임을 알 수 있다. 즉, 상관계수($\rho$)가 낮다. Risk-Parity 투자 전략은 두 자산의 변동성에 따른 손실을 방어하며 개별 자산보다 안정적인 수익률을 제공할 것이다.

2. SPY와 IEF는 각각 S&P500 지수와 미국 7~10년 장기국채 지수를 추종하는 ETF 상품이다. 즉, 주식과 채권으로 Risk-Parity 투자 전략을 구현하는데 있어서 leverage ETF 상품은 필수로 요구되지 않는다. 그러나, 채권의 변동성이 주식의 변동성에 비해 확연히 낮다는 것을 고려한다면, 상단의 SPY와 IEF로 구현된 Risk-Parity 투자 전략은 IEF에 막대한 비중을 투자할 것이다. 이에 따라, 미국 장기국채에 투자하는 것이나 다를 바 없는, 안정적이지만 수익률이 매우 낮은 투자 전략이 구현될 것이다. 이를 방지하기 위해 3X leverage ETF 상품을 선정하였다.

3. 금리에 따른 채권의 가격 변화는 $\frac{\triangle P}{P} = -MD *\triangle y$이다. 즉, duration이 긴 채권일수록 금리 변화에 따른 채권의 가격 변화는 커진다. 이에 기반해, 미국 7~10년 장기국채 지수 대신, 기간이 더 긴 20년 장기국채 지수를 추종하는 ETF 상품을 선정했다. 채권의 가격 변화는 변동성으로 이어지며, 미국 20년 장기국채 지수의 폭넓은 변동성은 Risk-Parity 투자 전략이 주식과 채권에 유기적인 비중으로 투자하도록 도울 것이다.

데이터 특성 및 설명

특성	설명
주식	TQQQ
채권	TMF
BM	SPY
단위	1개월 단위 데이터
기간	2010/03/01 ~ 2021/12/01
출처	Yahoo Finance
파일 형식	Excel(rawdata.xlsx)

데이터 구성 예시

Date	TQQQ	TMF	SPY
2010-03-01	1.16	7.63	117
2010-04-01	1.23	8.39	118.81
2010-05-01	0.95	9.78	109.37
$\cdots$	$\cdots$	$\cdots$	$\cdots$
2021-10-01	155.16	28.14	459.25
2021-11-01	163.49	30.22	464.6
2021-12-01	167.44	29.91	464.6

# Extract excel data  

data_excel = pd.ExcelFile('./rawdata.xlsx')
  
# Convert rawdata to dataframe

data_df = data_excel.parse(sheet_name='Sheet1', index_col='Date') # Excel to dataframe
rawTime = data_df.index.copy() # Time to dataframe
rawTQQQ = data_df.iloc[:, 0].copy() # TQQQ to dataframe
rawTMF = data_df.iloc[:, 1].copy() # TMF to dataframe
rawBM = data_df.iloc[:, 2].copy() # BM to dataframe 
  
# Return dataframe
rawR1 = rawTQQQ.pct_change()*100
rawR2 = rawTMF.pct_change()*100

2. Risk-Parity

🚫 함수(def)로 구성되지 않았음.

# Back-testing

stDateNum = 20110501 # Back-test starting date
stDate = pd.to_datetime(str(stDateNum), format='%Y%m%d')

# Calculate standard deviation

tau = 12 # 12 month standard deviation calculation

rawSigma1 = rawR1.rolling(tau).std()
rawSigma2 = rawR2.rolling(tau).std()


# Weight dataframe
  
rawWeight1 = rawSigma2 / (rawSigma1 + rawSigma2)
rawWeight2 = 1 - rawWeight1

# Slice dataframes to back-test starting date  
  
Time = rawTime[rawTime>=stDate].copy()
R1 = rawR1[rawR1.index>=stDate].copy()
R2 = rawR2[rawR2.index>=stDate].copy()
Weight1 = rawWeight1[rawWeight1.index>=stDate].copy()
Weight2 = rawWeight2[rawWeight2.index>=stDate].copy()

numData = R1.shape[0] # Length of data used in back-testing
  
# Portfolio return & value series
  
Rp = pd.Series(np.zeros(numData)) # Return series
Vp = pd.Series(np.zeros(numData)) # Value series
Vp[0] = 100 # Initial amount invested in RP portfolio

for t in range(1,numData):
    Rp[t] = Weight1[t-1]*R1[t] + Weight2[t-1]*R2[t] # Return calculation for RP
    Vp[t] = Vp[t-1]*(1 + Rp[t]/100) # Value calculation for RP

# Drawdown

MAXp = Vp.cummax()
DDp = (Vp/MAXp - 1)*100

3. Benchmark

🚫 함수(def)로 구성되지 않았음.

# Slice dataframes to back-test starting date

SP500 = rawBM[rawBM.index>=stDate].copy()

# Value calculation for BM
  
Vb = (SP500/SP500[0])*100

# Drawdown
  
MAXb = Vb.cummax()
DDb = (Vb/MAXb - 1)*100

4. Graphs

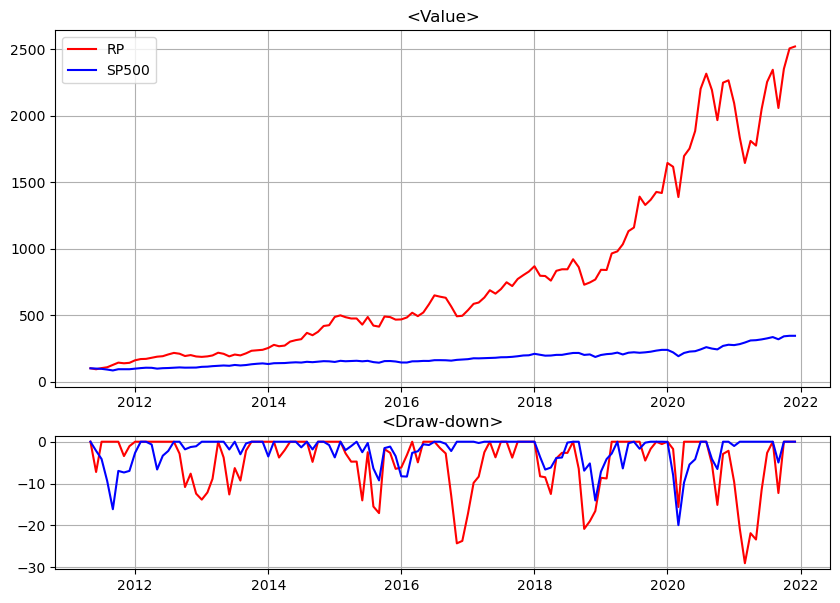
앞서 구현한 Risk-Parity 및 Benchmark 코드를 활용해 그래프로 시각화하였다.

RP 함수 구성 예시

파라미터	설명
data_Time	rawTime
data_Risky	rawRisky
return_Risky	rawR1
return_Rf	rawR2
stDate	'20110501'
stMoney	100

fig = plt.figure(figsize=(10, 7))   
gs = gridspec.GridSpec(nrows=2,     
                       ncols=1,    
                       height_ratios=[8, 3], 
                       width_ratios=[5]) 

ax0 = plt.subplot(gs[0])
ax0.plot(Time, Vp, label='RP', color='red')
ax0.plot(Time,Vb, label='SP500', color='blue')
ax0.set_title('<Value>')
ax0.grid(True)
ax0.legend()

ax1 = plt.subplot(gs[1])
ax1.plot(Time, DDp, color='red')
ax1.plot(Time, DDb, color='blue')
ax1.set_title('<Draw-down>')
ax1.grid(True)

plt.show()

Graph는 다음과 같이 도출된다:

📙 마치며

이상으로 Risk-Parity 투자 전략 포스트를 마치겠다.

출처:

Thumbnail Arrow:

본 포스트는 숭실대학교 금융학부 데이터 기반 투자전략 수업자료를 활용하여 제작되었습니다.
학부생으로서 직접 배운 것을 바탕으로 작성된 포스트로, 오류가 존재할 수 있습니다.

읽어주셔서 감사합니다 🥰