Day 66

Wed, Aug 09, 2023
Python_advanced day8

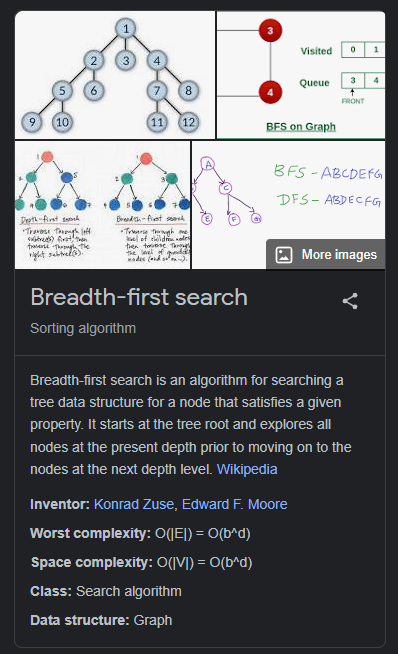
Breadth-First Search

from collections import deque

def bfs(graph, start_vertex):
    # Step 1: Initialize the list 'visited' to keep track of visited vertices.
    visited = [False] * len(graph)
    
    # Step 2: Initialize a queue (using a deque for efficient pop from left).
    queue = deque([start_vertex])
    
    # Mark the start_vertex as visited.
    visited[start_vertex] = True
    
    # Step 3: Begin the BFS loop.
    while queue:
        # Step 4: Get the next vertex from the left end of the queue.
        vertex = queue.popleft()
        
        # Step 5: Print the current vertex to show the traversal.
        print(vertex, end=" ")
        
        # Step 6: Iterate through all neighboring vertices of the current vertex.
        for i in graph[vertex]:
            # Step 7: Check if the neighboring vertex 'i' hasn't been visited yet.
            if not visited[i]:
                # Step 8: If 'i' hasn't been visited, add it to the queue and mark as visited.
                queue.append(i)
                visited[i] = True

Going through the provided graph and the BFS traversal starting from vertex 1.

graph = [
    [],
    [2, 3],
    [1, 8],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7, 8],
    [6, 8],
    [2, 6, 7]
]

start_vertex = 1
bfs(graph, start_vertex)

The graph is represented as an adjacency list. Each element in the 'graph' list corresponds to a vertex, and its value is a list of neighboring vertices. The index of the element represents the vertex number. For example, 'graph[1]' contains the neighbors of vertex 1.

Walking through the BFS traversal step by step:


1. Initialize 'visited' list to '[False, False, False, False, False, False, False, False, False]'.
2. Initialize the queue with the starting vertex: 'queue = [1]'.
3. Mark vertex 1 as visited: 'visited = [False, True, False, False, False, False, False, False, False]'.


Traversal steps:


1. Dequeue vertex 1. Print: '1'.
2. Neighbors of vertex 1 are '[2, 3]'.
- Vertex 2 is not visited. Enqueue and mark as visited.
- Vertex 3 is not visited. Enqueue and mark as visited.
- Queue: '[2, 3]'. Visited: '[False, True, True, True, False, False, False, False, False]'.
3. Dequeue vertex 2. Print: '2'.
4. Neighbors of vertex 2 are '[1, 8]'.
- Vertex 1 is already visited.
- Vertex 8 is not visited. Enqueue and mark as visited.
- Queue: '[3, 8]'. Visited: '[False, True, True, True, False, False, False, False, True]'.
5. Dequeue vertex 3. Print: '3'.
6. Neighbors of vertex 3 are '[1, 4, 5]'.
- Vertex 1 is already visited.
- Vertex 4 is not visited. Enqueue and mark as visited.
- Vertex 5 is not visited. Enqueue and mark as visited.
- Queue: '[8, 4, 5]'. Visited: '[False, True, True, True, True, True, False, False, True]'.
7. Dequeue vertex 8. Print: '8'.
8. Neighbors of vertex 8 are '[2, 6, 7]'.
- Vertex 2 is already visited.
- Vertex 6 is not visited. Enqueue and mark as visited.
- Vertex 7 is not visited. Enqueue and mark as visited.
- Queue: '[4, 5, 6, 7]'. Visited: '[False, True, True, True, True, True, True, True, True]'.
9. Dequeue vertex 4. Print: '4'.
10. Vertex 4 has neighbors '[3, 5]', both of which are already visited.
11. Dequeue vertex 5. Print: '5'.
12. Vertex 5 has neighbors '[3, 4]', both of which are already visited.
13. Dequeue vertex 6. Print: '6'.
14. Vertex 6 has neighbors '[7, 8]', both of which are already visited.
15. Dequeue vertex 7. Print: '7'.
16. Vertex 7 has neighbors '[6, 8]', both of which are already visited.

The BFS traversal starting from vertex 1 results in the order of visited vertices: '1 2 3 8 4 5 6 7'.

This traversal explores vertices in layers, moving from the starting vertex to its immediate neighbors, then to their neighbors, and so on. It guarantees that vertices closer to the starting vertex are visited before vertices farther away.