Machine Learning Day 16
* Decision Tree - is used for distinguishing Feature Importance
* KNN Clustering - is used for pre-training of YOLO(You Only Look Once) Algorithm
* Bayesian Inference - relationship between Prior Probability and Posterior Probability
=> These things matter for understanding the concept of what Algorithm is.
- Bayesian Inference = a step for better understanding of Gausian Algorithm
<Exercise.1>
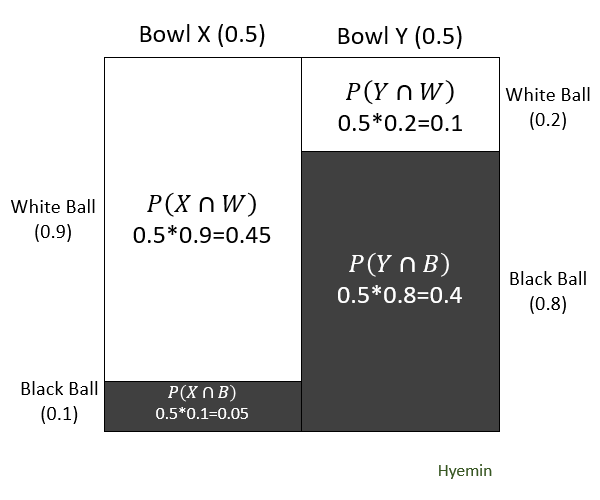
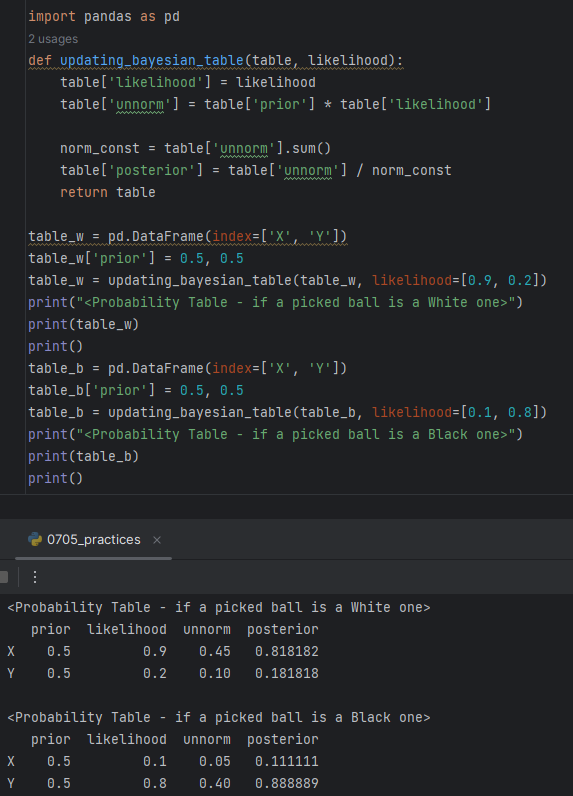
- Posterior Probabilities
P(X∣W)=P(W)P(X)⋅P(W∣P)=P(X∩W)+P(Y∩W)P(X∩W)=P(X)⋅P(W∣X)+P(Y)⋅P(W∣Y)P(X)⋅P(W∣X) P(X∣B)=P(B)P(X)⋅P(B∣X)=P(X∩B)+P(Y∩B)P(X∩B)=P(X)⋅P(B∣X)+P(Y)⋅P(B∣Y)P(X)⋅P(B∣X) P(Y∣W)=P(W)P(Y)⋅P(W∣Y)=P(X∩W)+P(Y∩W)P(Y∩W)=P(X)⋅P(W∣X)+P(Y)⋅P(W∣Y)P(Y)⋅P(W∣Y) P(Y∣B)=P(B)P(Y)⋅P(B∣Y)=P(X∩B)+P(Y∩B)P(Y∩B)=P(X)⋅P(B∣X)+P(Y)⋅P(B∣Y)P(Y)⋅P(B∣Y)
<Exercise.2>
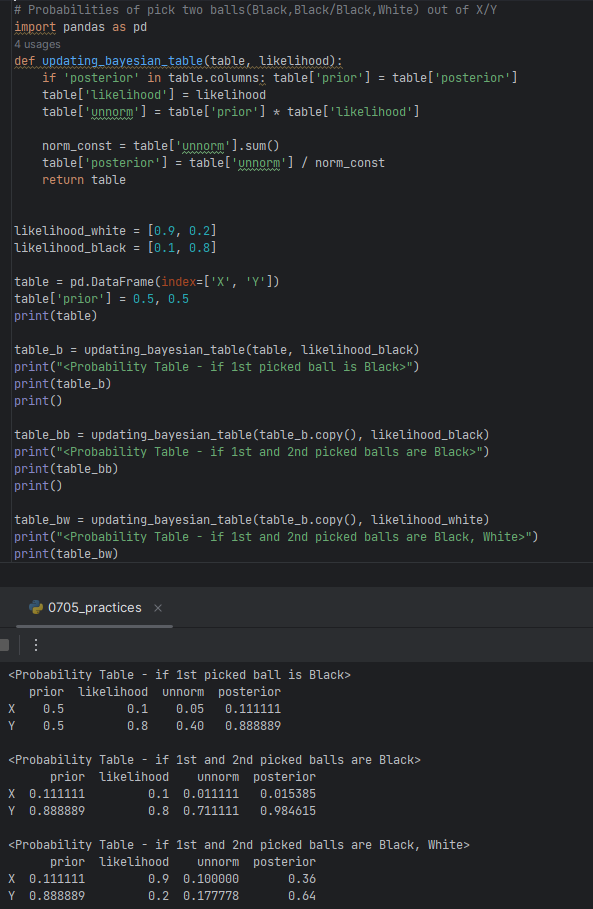
<Exercise.3>
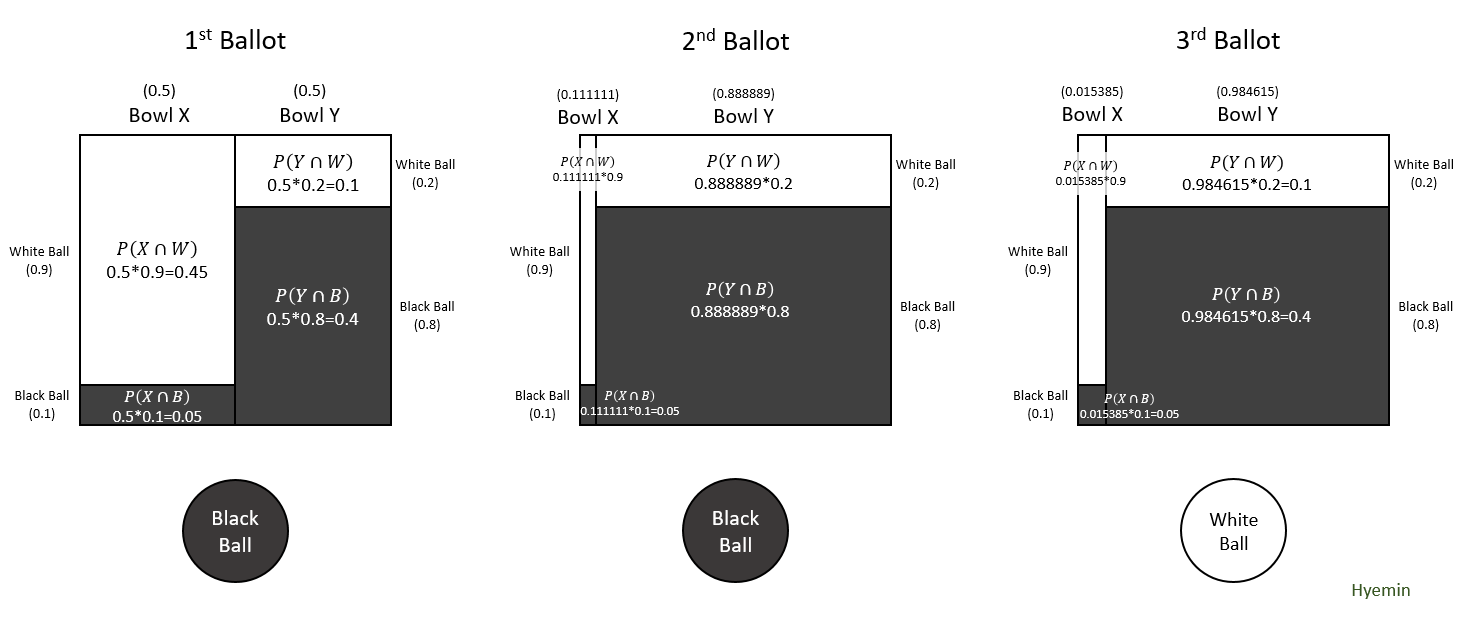
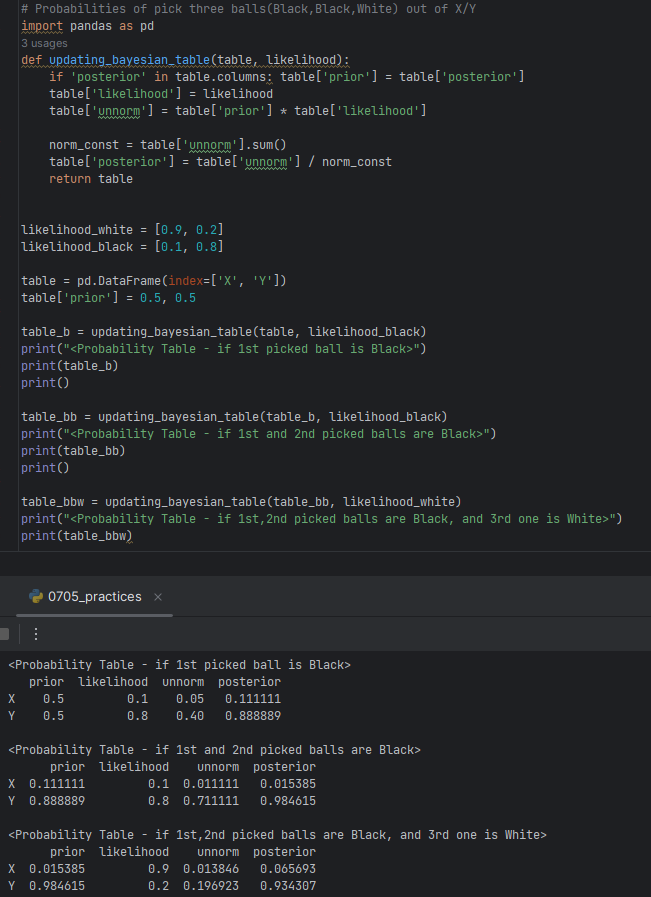
- Naive Bayes: Bayes Inference just assumes that A and B are Independent even though the two have some degree of dependence.
e.g) "Investment" and "Return-Rate" can be dependent within a context although they are the two very different words.






