[백준] 17471번 - 게리맨더링

야금야금 공부·2024년 9월 8일
골드3
0

백준

목록 보기
50/52

https://www.acmicpc.net/problem/17471

문제

백준시의 시장 최백준은 지난 몇 년간 게리맨더링을 통해서 자신의 당에게 유리하게 선거구를 획정했다. 견제할 권력이 없어진 최백준은 권력을 매우 부당하게 행사했고, 심지어는 시의 이름도 백준시로 변경했다. 이번 선거에서는 최대한 공평하게 선거구를 획정하려고 한다.

백준시는 N개의 구역으로 나누어져 있고, 구역은 1번부터 N번까지 번호가 매겨져 있다. 구역을 두 개의 선거구로 나눠야 하고, 각 구역은 두 선거구 중 하나에 포함되어야 한다. 선거구는 구역을 적어도 하나 포함해야 하고, 한 선거구에 포함되어 있는 구역은 모두 연결되어 있어야 한다. 구역 A에서 인접한 구역을 통해서 구역 B로 갈 수 있을 때, 두 구역은 연결되어 있다고 한다. 중간에 통하는 인접한 구역은 0개 이상이어야 하고, 모두 같은 선거구에 포함된 구역이어야 한다.

아래 그림은 6개의 구역이 있는 것이고, 인접한 구역은 선으로 연결되어 있다.

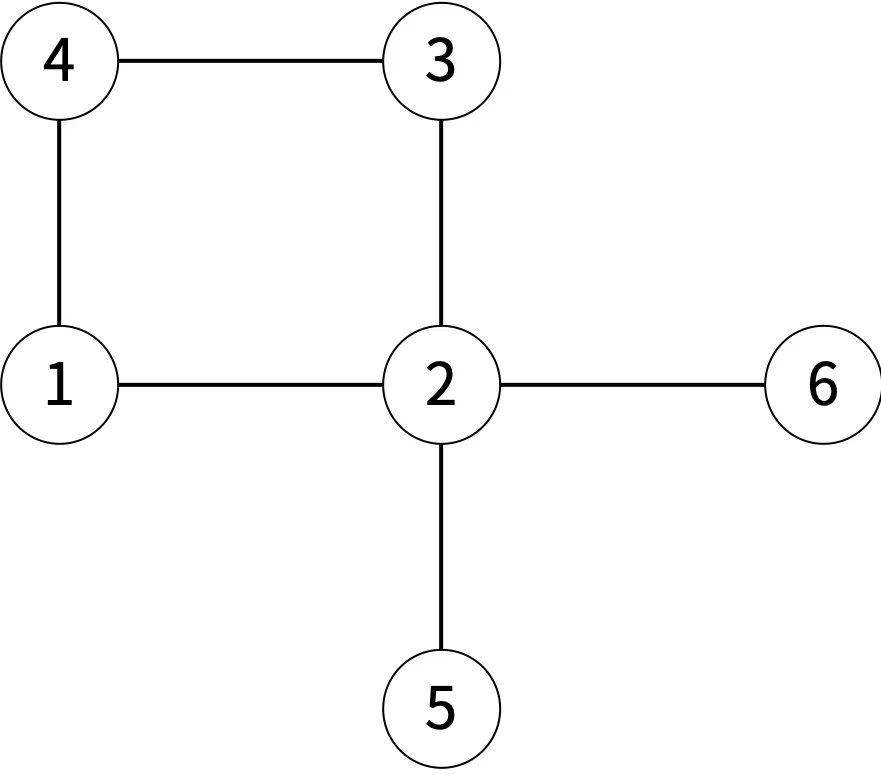
아래는 백준시를 두 선거구로 나눈 4가지 방법이며, 가능한 방법과 불가능한 방법에 대한 예시이다.

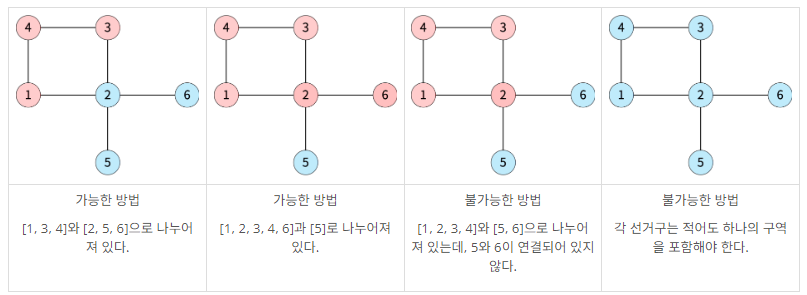
공평하게 선거구를 나누기 위해 두 선거구에 포함된 인구의 차이를 최소로 하려고 한다. 백준시의 정보가 주어졌을 때, 인구 차이의 최솟값을 구해보자.

입력

첫째 줄에 구역의 개수 N이 주어진다. 둘째 줄에 구역의 인구가 1번 구역부터 N번 구역까지 순서대로 주어진다. 인구는 공백으로 구분되어져 있다.

셋째 줄부터 N개의 줄에 각 구역과 인접한 구역의 정보가 주어진다. 각 정보의 첫 번째 정수는 그 구역과 인접한 구역의 수이고, 이후 인접한 구역의 번호가 주어진다. 모든 값은 정수로 구분되어져 있다.

구역 A가 구역 B와 인접하면 구역 B도 구역 A와 인접하다. 인접한 구역이 없을 수도 있다.

출력

첫째 줄에 백준시를 두 선거구로 나누었을 때, 두 선거구의 인구 차이의 최솟값을 출력한다. 두 선거구로 나눌 수 없는 경우에는 -1을 출력한다.

제한

2 ≤ N ≤ 10
1 ≤ 구역의 인구 수 ≤ 100

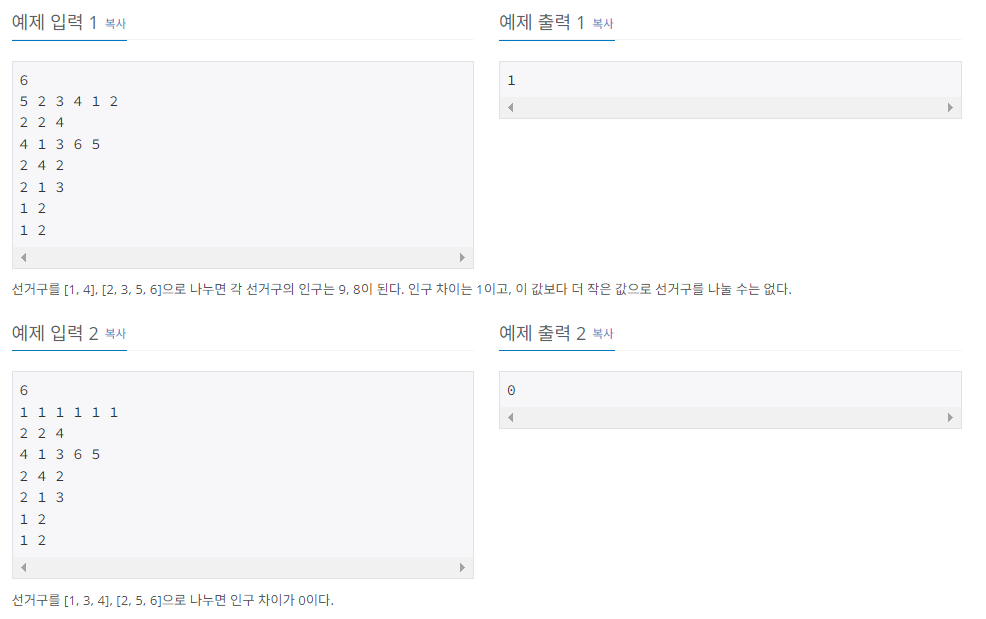
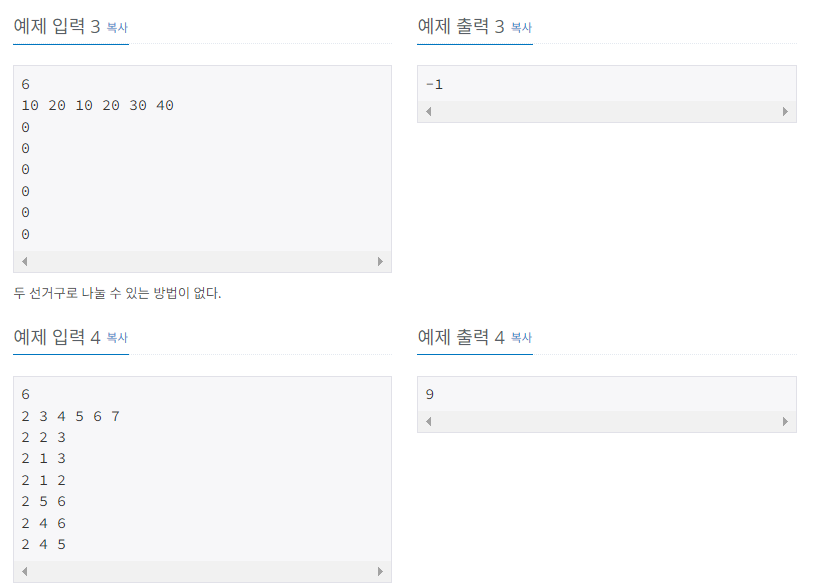
문제 풀이

  • 선거구 나누는 부분이 어려워서 검색했더니, 비트 마스크로 풀이하는 코드가 나왔다.

비트마스크 이해하기

  • 예시: n = 4일 경우
    n = 4일 때, 4개의 구역이 있습니다. 즉, 구역 번호는 0, 1, 2, 3입니다.
    i는 1부터 (1 << n) - 1까지 순회하는데, (1 << n)은 2의 n승, 즉 16입니다.
    (1 << n) - 1은 15가 되어, i는 1부터 15까지 값이 됩니다.
    i를 이진수로 나타내면, 각 비트는 구역이 선택되었는지를 나타냅니다.
    i 값에 따른 부분 집합 예시:
  • i = 1 (이진수: 0001): 구역 0만 선택
  • i = 2 (이진수: 0010): 구역 1만 선택
  • i = 3 (이진수: 0011): 구역 0과 1 선택
  • i = 15 (이진수: 1111): 모든 구역 선택
    즉, i의 각 비트는 구역이 그룹 A에 포함될지 여부를 나타냅니다.

비트 연산으로 부분 집합 구하기

if ((i & (1 << j)) > 0) {
    groupA.add(j);
} else {
    groupB.add(j);
}
  • 1 << j는 1을 왼쪽으로 j만큼 이동시킨 이진수입니다. 예를 들어, j = 2라면 1 << 2는 0100이 됩니다.
  • (i & (1 << j)) > 0는 i의 j번째 비트가 1인지 확인하는 연산입니다.
  • i의 j번째 비트가 1이라면 groupA에 j 구역을 추가합니다.
  • j번째 비트가 0이라면 groupB에 추가합니다.

이 방식으로 모든 구역을 두 개의 그룹으로 나누게 됩니다.

  • 예시: i = 5 (이진수: 0101)
    • j = 0: i & (1 << 0) = 1 & 1 → 1 → 구역 0은 groupA
    • j = 1: i & (1 << 1) = 1 & 2 → 0 → 구역 1은 groupB
    • j = 2: i & (1 << 2) = 4 & 5 → 4 → 구역 2는 groupA
    • j = 3: i & (1 << 3) = 0 & 5 → 0 → 구역 3은 groupB

즉, i = 5일 때, 구역 0과 2는 groupA에, 구역 1과 3은 groupB에 속하게 됩니다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;

/*
1. 부분 집합 구하기
2. 두 그룹관 연결성 확인
3. 인구 차이 계산
4. 최소 인구 차이 찾기
 */
public class Solution {

	private static int n, r;
	private static int[] population;
	private static int[] parents;
	private static List<Integer>[] link;

	public static void main(String[] args) throws Exception {

		BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

		n = Integer.parseInt(in.readLine());
		population = new int[n]; // 인구수
		parents = new int[n];
		link = new ArrayList[n];

		String[] split = in.readLine().split(" ");
		for (int i = 0; i < n; i++) {
			population[i] = Integer.parseInt(split[i]);
		}

		for (int i = 0; i < n; i++) {
			link[i] = new ArrayList<>();
		}

		// 인접 구역 수 : 인접 구역 번호
		for (int i = 0; i < n; i++) {
			split = in.readLine().split(" ");
			int cnt = Integer.parseInt(split[0]);
			for (int j = 1; j <= cnt; j++) {
				link[i].add(Integer.parseInt(split[j]) - 1);
			}
		}


		int ans = Integer.MAX_VALUE;  
        // 선거구를 두 구역으로 분리
		for (int i = 1; i < (1 << n) - 1; i++) {
			List<Integer> groupA = new ArrayList<Integer>();
			List<Integer> groupB = new ArrayList<Integer>();
			
            // 부분 집합 구하기
			for (int j = 0; j < n; j++) {
				if ((i & (1 << j)) > 0) {
					groupA.add(j);
				} else {
					groupB.add(j);
				}
			}
			
            // 두 그룹이 연결되있는 지 확인
			if (isConneccted(groupA) && isConneccted(groupB)) {
				ans = Math.min(ans, calcuDiff(groupA, groupB));
			}
		}

		System.out.println(ans == Integer.MAX_VALUE ? -1 : ans);

	}

	// bfs : 그룹이 연결되어 있는지 확인하는 함수
	private static boolean isConneccted(List<Integer> group) {

		boolean[] visited = new boolean[n];
		Queue<Integer> queue = new ArrayDeque<>();
		queue.add(group.get(0));
		visited[group.get(0)] = true;
		int cnt = 1;

		while (!queue.isEmpty()) {
			int curr = queue.poll();
			for (int next : link[curr]) {
				if (!visited[next] && group.contains(next)) {
					visited[next] = true;
					queue.add(next);
					cnt++;
				}
			}
		}

		return cnt == group.size(); // 모든 노드가 연결되었는지 확인
	}

	// 인구수 차이 계산
	public static int calcuDiff(List<Integer> groupA, List<Integer> groupB) {

		int populA = 0, populB = 0;

		for (int g : groupA) {
			populA += population[g];
		}

		for (int g : groupB) {
			populB += population[g];
		}

		return Math.abs(populA - populB);
	}

}

문제 풀이2

  • union-find 로 풀기
package algo.practice;

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
import java.util.StringTokenizer;

/*
1. 부분 집합 구하기
2. 두 그룹관 연결성 확인
3. 인구 차이 계산
4. 최소 인구 차이 찾기
 */
public class M_17471_게리맨더링_비트마스크 {

	private static int n, r;
	private static int[][] graph;
	private static int[] population;
	private static boolean[] selected;
	private static int[] parents;
	private static int answer = Integer.MAX_VALUE;

	public static void main(String[] args) throws Exception {

		BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;

		n = Integer.parseInt(in.readLine());
		graph = new int[n][n];
		population = new int[n]; // 인구수
		parents = new int[n];
		selected = new boolean[n];

		String[] split = in.readLine().split(" ");
		for (int i = 0; i < n; i++) {
			population[i] = Integer.parseInt(split[i]);
		}

		// 인접 구역 수 : 인접 구역 번호
		for (int from = 0; from < n; from++) {
			st = new StringTokenizer(in.readLine());
			int cnt = Integer.parseInt(st.nextToken()); // Number of adjacent districts
			for (int i = 0; i < cnt; i++) {
				int to = Integer.parseInt(st.nextToken()) - 1; // Convert to 0-based index
				graph[from][to] = 1;
			}
		}

		subSet(0);
		System.out.println(answer == Integer.MAX_VALUE ? -1 : answer);

	}

	private static void subSet(int r) {

		if (r == n) {
			List<Integer> group1 = new ArrayList<>();
			List<Integer> group2 = new ArrayList<>();

			for (int i = 0; i < n; i++) {

				if (selected[i]) {
					group1.add(i);
				} else {
					group2.add(i);
				}
			}

			if (group1.size() == 0 || group2.size() == 0) {
				return;
			}

			makeSet();
			distribute(group1);
			distribute(group2);

			if (isConnected(group1, group2)) {
				int sum1 = populSum(group1);
				int sum2 = populSum(group2);
				answer = Math.min(answer, Math.abs(sum1 - sum2));
			}

			return;

		}

		selected[r] = true;
		subSet(r + 1);
		selected[r] = false;
		subSet(r + 1);

	}

	private static int populSum(List<Integer> group) {
		int sum = 0;
		for (int idx : group) {
			sum += population[idx];
		}

		return sum;
	}

	private static void distribute(List<Integer> group) {
		for (int from : group) {
			for (int to : group) {
				if (from != to && graph[from][to] == 1) {
					union(from, to);
				}
			}
		}
	}

	private static boolean isConnected(List<Integer> group1, List<Integer> group2) {

		int root1 = find(group1.get(0));
		for (int i = 1; i < group1.size(); i++) {
			if (find(group1.get(i)) != root1) {
				return false;
			}
		}

		int root2 = find(group2.get(0));
		for (int i = 1; i < group2.size(); i++) {
			if (find(group2.get(i)) != root2) {
				return false;
			}
		}

		return true;
	}

	private static void makeSet() {
		for (int i = 0; i < n; i++) {
			parents[i] = i;
		}
	}

	private static int find(int u) {
		if (parents[u] == u) {
			return u;
		}
		return parents[u] = find(parents[u]);
	}

	private static void union(int u, int v) {
		int rootU = find(u);
		int rootV = find(v);
		if (rootU != rootV) {
			parents[rootV] = rootU; // Union by setting one root as the parent of the other
		}
	}

}

참고 블로그

profile
야금야금 공부
이전 포스트

[백준] 10775번 - 공항

다음 포스트

[백준] 2606번 - 바이러스

0개의 댓글