[SWEA] 11315. 오목 판정

11315. 오목 판정

문제 풀이

총 4가지 경우를 고려해주어야 한다.

• 가로, 세로
• 오른쪽 아래로 가는 대각선
• 왼쪽 위로 가는 대각선

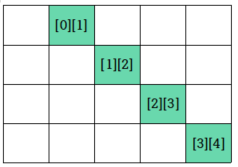
1. 오른쪽 아래로 가는 대각선일 경우
예시가 $n=5$라서, i = j 로 혼동하기 쉽다.
$(i, j)$에서 시작하는 대각선은 $(i + 1, j + 1)$ 이다.

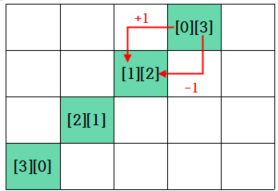
2. 왼쪽 위로 가는 대각선일 경우
이 경우도 처음에 $(i - j) = (n-1)$로 생각해 오답이 발생하였다.
$(i, j)$에서 시작하는 대각선은 $(i+1, j-1)$이 된다.

제출 코드

# 테스트 케이스 개수
t = int(input())

# 오른쪽 아래 대각선
def rl_digo(i, j):

    ans = False

    a = cnt = 0
    # 연속되는 대각선의 'o'의 개수(cnt)를 출력
    while arr[i + a][j + a] == 'o' and 0 <= i + a < n and 0 <= j + a < n:
        cnt += 1
        a += 1
		
        # 개수가 5면 True를 return
        if cnt == 5:    
            ans = True
            return ans
		
        # 범위를 초과하면 break
        if i + a >= n or j + a >= n:
            break

    return ans


# 왼쪽 아래 대각선
def lr_diago(i, j):
    ans = False

    a = cnt = 0
    # 연속되는 대각선의 'o'의 개수(cnt)를 출력
    while arr[i + a][j - a] == 'o' and 0 <= i + a < n and 0 <= j - a < n:
        cnt += 1
        a += 1
		
        # 개수가 5면 True를 return
        if cnt == 5:
            ans = True
            return ans
		
        # 범위 초과하면 break
        if i + a >= n or j - a < 0:
            break

    return ans


# 가로, 세로
def garo_sero(i, j):
    ans = False

    s_cnt = g_cnt = 0
    a = 0
    # 연속되는 가로에 'o'의 개수
    while arr[i][j + a] == 'o':
        g_cnt += 1
        a += 1
		
        # 개수가 5개면 True 리턴
        if g_cnt == 5:
            ans = True
            return ans
            
        if j + a >= n:
            break
	
    # 연속되는 세로에 'o'의 개수
    a = 0
    while arr[j + a][i] == 'o':
        s_cnt += 1
        a += 1
		
        # 개수가 5면 True 리턴
        if s_cnt == 5:
            ans = True
            return ans

        if j + a >= n:
            break

    return ans


for k in range(1, t + 1):

    n = int(input())
    arr = [list(input()) for _ in range(n)]
    ans = False
	
    
    for i in range(n):
        for j in range(n):  
        
        	# 'o'의 위치에서 대각선, 가로, 세로 모두 확인
            if arr[i][j] == 'o' and rl_digo(i, j) or lr_diago(i, j) or garo_sero(i, j):
            
                ans = True  # 하나라도 True면 ans는 True
                break

    if ans:     # True이면 정답은 YES
        print(f"#{k} YES")

    else:       # False면 정답은 NO
        print(f"#{k} NO")

5x5 배열이라고 생각해 풀었더니 오답이 자꾸 발생하였다.

아래는 if arr[i][j] == 'o' 안에서 if 대각선, 가로, 세로를 확인하였더니 99만 정답인 모습
이때 조금 어이없었다.
break는 1개의 for문을 빠져나올 수 있어서 발생하는 오류였다. break의 범위를 잘 생각해서 구현해야 한다.

---

다른 코드

• dr, dc를 활용해 좀 더 간결하게 구현하였다.
  방향이 일정하게 정해져있는 문제라서 이 방법으로 푸는 것도 가능한 것 같다.

# '.' : 돌이 없는 칸, 'o' : 돌이 있는 칸
# 오른쪽, 오른쪽아래대각선, 아래쪽, 왼쪽아래대각선으로 연속 5개나와야함

# arr에 오목이 존재하면 'YES', 존재하지 않으면 'NO' return
def A(arr):
    # 우,하,우하대,좌하대
    dr = [0,1,1,1]
    dc = [1,0,1,-1]
    for start_r in range(N):
        for start_c in range(N):
            if arr[start_r][start_c] == 'o':
                for d in range(4):
                    r = start_r
                    c = start_c
                    # 각 방향으로 연속적으로 오목이 존재하는가?
                    cnt = 0
                    # 파이썬만 0 <= r <= N-1 허용
                    # 다른 언어는 r >= 0 and r <= N-1
                    while 0 <= r <= N-1 and 0 <= c <= N-1 and arr[r][c] == 'o':
                        cnt += 1
                        r += dr[d]
                        c += dc[d]
                    # 각 방향으로 오목이 존재?하는가
                    if cnt >= 5:
                        return 'YES'
    return 'NO'

# 테스트 케이스의 개수
T = int(input())
for tc in range(1,T+1):
    # N*N 크기의 판
    N = int(input())
    arr = [input() for _ in range(N)]

    print(f'#{tc} {A(arr)}')

---

참고 블로그

• 코드 참고 블로그