딥러닝 Deeplearning 5

Bleu·2023년 10월 18일
notepython
0

python

목록 보기
21/22

DNN (Deep Neural Network)

==MLP (Multi Layer Perceptron) == ANN(Artigicial Neural Network) == 선형회귀 함수를 사용

신경망 구성요소

Train(학습) 프로세스

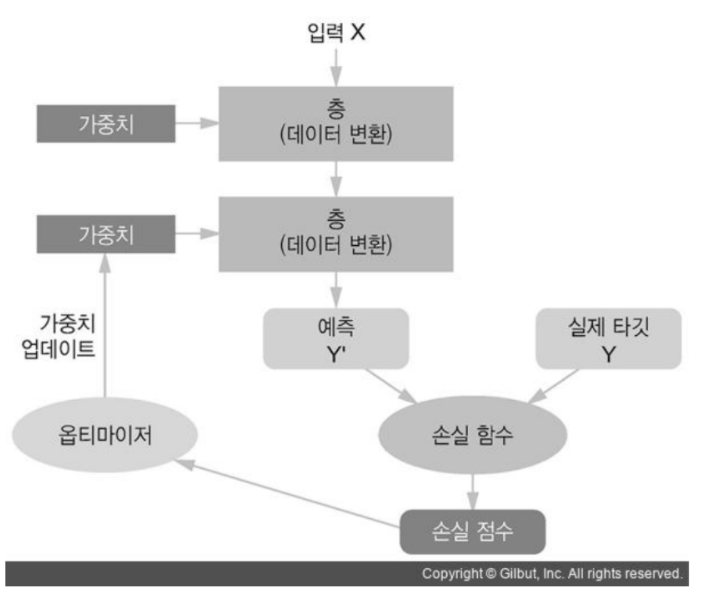
역할

  1. Model/Network
    • 기존 데이터의 패턴을 학습하여 새로운 데이터를 추론하기 위한 알고리즘, 함수.
  2. Loss Function (손실 함수)
    • 학습 할 때 모델이 추론한 결과와 정답(Ground truth)간의 Loss(손실/오차)를 계산한다.
  3. Optimizer(옵티마이저)
    • 학습 할 때 loss function이 계산한 Loss를 기반으로 Loss가 줄어들도록 모델의 파라미터들(weight)을 업데이트하여 모델의 성능을 최적화한다.

유닛/노드/뉴런 (Unit, Node, Neuron)

  • Input data를 입력받아 처리 후 출력하는 데이터 처리하는 함수.
    • Hidden layer(은닉층)의 Unit들은 입력으로 부터 추론을 위한 주요 특성들을 찾아 출력한다.
    • Output layer(출력층)의 Unit들은 추론 결과를 출력한다.
  • Input data의 Feature들에 Weight(가중치)를 곱하고 bias(편향)을 더한 결과를 Activation 함수에 넣어 출력하는 계산을 처리한다.

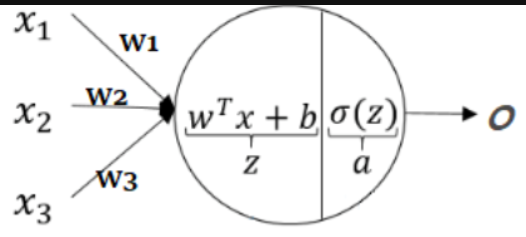
  • Input vector(입력값): x=(x1,x2,x3)T\large\mathbb x=(x_1, x_2, x_3)^T
  • Weights(가중치): w=(w1,w2,w3)T\large\mathbb w = (w_1, w_2, w_3)^T
  • Bias(편향): b∈R\large b \in \mathbb R
  • Activation function(활성함수): σ(z)\large\sigma(z)
    • 선형결합한 결과를 비선형화 시키는 목적
    • 다양한 비선형 함수들을 사용한다.


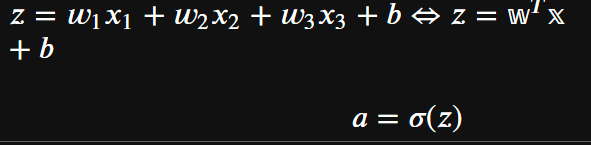
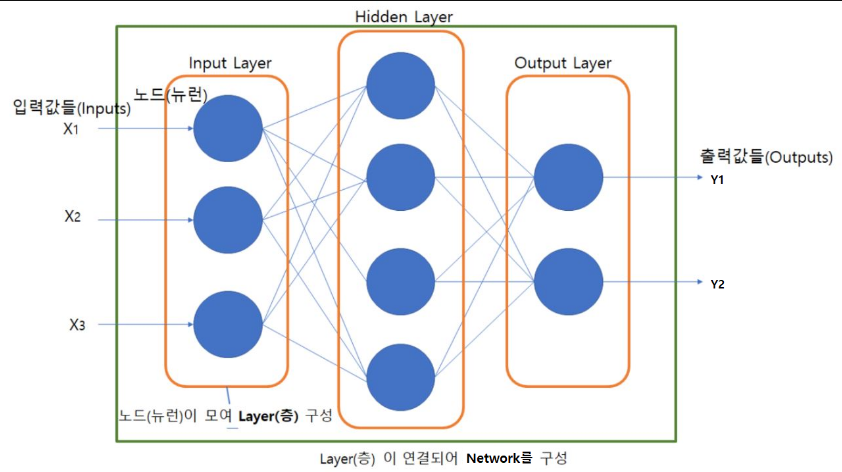
레이어/층(Layer)

  • 네트워크 모델의 각 처리단계를 정의한 함수.
    • 실제 처리를 담당하는 Unit들을 모아놓은 구조
  • Input Layer(입력층)
    • 입력값들을 받아 Hidden Layer에 전달하는 노드들로 구성된 Layer.
    • 입력 데이터의 shape을 설정하는 역할을 한다.
  • Output Layer(출력층)
    • 모델의 최종 예측결과를 출력하는 노드들로 구성된 Layer
  • Hidden Layer(은닉층)
    • Input Layer와 Output Layer사이에 존재하는 Layer.
  • 대부분 Layer들은 학습을 통해 최적화할 Paramter를 가짐
    • Dropout, Pooling Layer와 같이 Parameter가 없는 layer도 있다.
  • Layer들의 연결한 것을 Network 라고 한다.
    • 딥러닝은 Layer들을 깊게 쌓은 것을 말한다.(여러 Layer들을 연결한 것)

  • 목적, 구현 방식에 따라 다양한 종류의 Layer들이 있다.

    • Fully Connected Layer (Dense layer)
      • 추론 단계에서 주로 사용
    • Convolution Layer
      • 이미지 Feature extraction으로 주로 사용
    • Recurrent Layer
      • Sequential(순차) 데이터의 Feature extraction으로 주로 사용
    • Embedding Layer
      • Text 데이터의 Feature extraction으로 주로 사용 - 숫자료 바꿈

  • API


모델 (Network)

  • Layer를 연결한 것이 Deep learning 모델다.
  • 이전 레이어의 출력을 input으로 받아 처리 후 output으로 출력하는 레이어들을 연결한다.
  • 적절한 network 구조(architecture)를 찾는 것은 공학적이기 보다는 경험적(Art)접근이 필요하다.

활성 함수 (Activation Function)

  • 각 유닛이 입력과 Weight간에 가중합을 구한 뒤 출력결과를 만들기 위해 거치는 함수
  • 같은 층(layer)의 모든 유닛들은 같은 활성 함수를 가진다.
  • 출력 레이어의 경우 출력하려는 문제에 맞춰 활성함수를 결정한다.
  • 은닉층 (Hidden Layer)의 경우 비선형성을 주어 각 Layer가 처리하는 일을 분리하는 것을 목적으로 한다.
    • 비선형함수를 사용하지 않으면 Layer들을 여러개 추가하는 의미가 없어진다.
    • ReLU 함수를 주로 사용한다.

주요 활성함수(Activation Function)

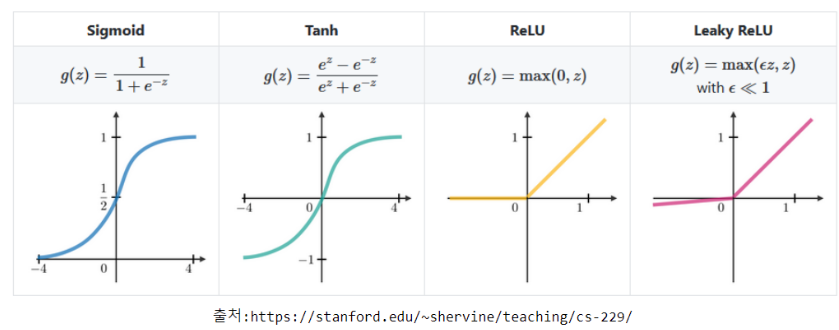
  • Sigmoid (logistic function)

    • σ(z)=11+e−z\large \sigma(z) = \frac 1 {1+e^{-z}}
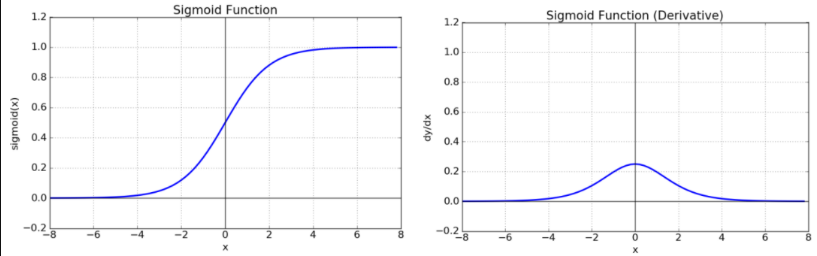
    • 출력값의 범위
      • 0<sigmoid(z)<10<sigmoid(z)<1
    • 한계
      • 초기 딥러닝의 hidden layer(은닉층)의 activation function(활성함수)로 많이 사용 되었다.
      • 층을 깊게 쌓을 경우 기울기 소실(Gradient Vanishing) 문제를 발생시켜 학습이 안되는 문제가 있다.
    • Binary classification(이진 분류)를 위한 네트워크의 Output layer(출력층)의 활성함수로 사용된다.
      • 모델이 positive(1)의 확률을 출력결과로 추론하도록 할 경우 사용. (unit개수 1, activation함수 sigmoid)
      • 위와 같은 한계때문에 hidden layer(은닉층)의 activation function(활성함수)로는 잘 사용되지 않는다.

기울기 소실(Gradient Vanishing) 문제란

  • 최적화 과정에서 gradient가 0이 되어서 Bottom Layer의 가중치들이 학습이 안되는 현상
    • Bottom Layer: Input Layer(입력층)에 가까이 있는 Layer들.
    • Top layer: Output Layer(출력층)에 가까이 있는 Layer들.

  • Hyperbolic tangent

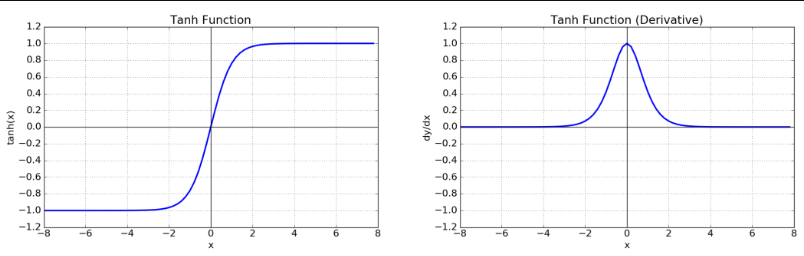
  • tanh(z)=ez−e−zez+e−z\large tanh(z) = \cfrac{e^{z} - e^{-z}}{{e^{z} + e^{-z}}}
  • 출력값의 범위
    • −1<tanh(z)<1-1<tanh(z)<1
  • Output이 0을 중심으로 분포하므로 sigmoid보다 학습에 효율 적이다.
  • 기울기 소실(Gradient Vanishing) 문제를 발생시킨다.

  • ReLU(Rectified Linear Unit)


    ReLU(z)=max(0,z)\large ReLU(z)=max(0,z)
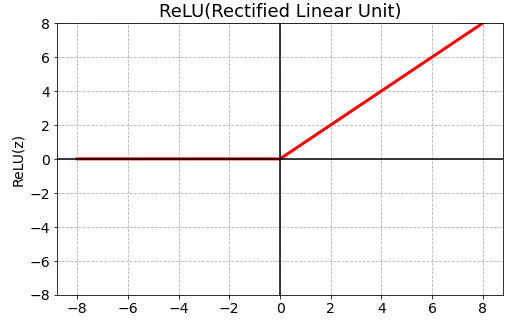
    - 기울기 소실(Gradient Vanishing) 문제를 어느정도 해결
    - 0이하의 값(z <= 0)들에 대해 뉴런이 죽는 단점이 있다. (Dying ReLU)

  • Leaky ReLU



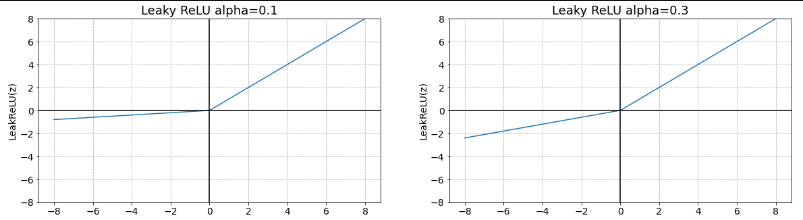
    LeakyReLU(z)=max(αz,z)0<α<1\large LeakyReLU(z)=max(\alpha z,z)\\ 0< \alpha <1



    • ReLU의 Dying ReLU 현상을 해결하기 위해 나온 함수
    • 음수 z를 0으로 반환하지 않고 alpah (0 ~ 1 사이 실수)를 곱해 반환한다.

  • Softmax

    Softmax(zj)=exp(zj)∑k=1Kexp(zk) j=1,2,…,K\large Softmax(z_j) = \frac{exp(z_j)}{\sum_{k=1}^K exp(z_k)}\\ \:j=1,2, \ldots, K
    • Multi-class classification(다중 분류)를 위한 네트워크의 Output layer(출력층)의 활성함수로 주로 사용된다.
      • 은닉층의 활성함수로 사용하지 않는다.
    • Layer의 unit들의 출력 값들을 정규화 하여 각 class에 대한 확률값으로 변환한다.
      • 출력노드들의 값은 0 ~ 1사이의 실수로 변환되고 그 값들의 총합은 1이 된다.

손실함수(Loss function, 비용함수)

  • Model이 출력한 예측값(prediction) y^(i)\hat y^{(i)}와 실제 데이터(output) y(i)y^{(i)}의 차이를 계산하는 함수

  • 네트워크 모델을 훈련하는 동안 Loss 함수가 계산한 Loss값(손실)이 최소화 되도록 파라미터(가중치와 편향)을 업데이트한다.

    • 즉 Loss함수는 최적화 시작이 되는 값이다.

  • 네트워크 모델이 해결하려는 문제의 종류에 따라 다른 Loss함수를 사용한다.

  • 해결하려는 문제의 종류에 따라 표준적인 Loss function이 있다.

  • Classification (분류)

    - cross entropy (log loss) 사용
    log(모델이 출력한 정답에 대한 확률)\large log(모델이\,출력한\,정답에\,대한\,확률)

  • Binary classification (이진 분류)

    • 특정 클래스인지 아닌지를 추론하거나 두 개의 클래스 중 하나를 추론하는 문제.

      • 모델이 양성(1)의 확률을 출력하여 Threshold(보통 0.5) 보다 작으면 0, 크면 1로 예측한다.
      • ex) 환자인지 여부, 스팸메일인지 여부

    • Output Layer의 unit 개수를 1로 하고 activation 함수로 sigmoid를 사용하여 positive(1)의 확률로 예측 결과를 출력하도록 모델을 정의 한 경우 binary_crossentropy를 loss function으로 사용한다.

      • nn.BCELoss() loss function을 사용

    • Loss(y^(i),y(i))=−y(i)log(y^(i))−(1−y(i))log(1−y^(i))\large Loss(\hat y^{(i)} ,y^{(i)}) = - y^{(i)} log(\hat y^{(i)} ) - (1- y^{(i)}) log (1-\hat y^{(i)} )

      y(i)y^{(i)}: 실제 값(Ground Truth), y^(i)\hat y^{(i)}: 모델이 예측한 확률(Positive일 확률)

  • Multi-class classification (다중 클래스 분류)

    • 두 개 이상의 클래스를 분류

      • 추론 대상이 여러개이고 그중 하나를 정답으로 예측한다.

    • 예) 이미지를 0,1,2,...,9로 구분

    • categorical crossentropy를 loss function으로 사용

      • nn.CrossEntropyLoss() loss function 사용

    • $\large Loss(\hat y_c^{(i)} ,y^{(i)}) = - \sum_{c=1}^C y_c^{(i)} log(\hat y_c^{(i)} ) $

      y(i)y^{(i)}: 실제 값(Ground Truth), y^c(i)\hat y_c^{(i)}: 모델이 예측한 class별 예측확률

  • Regression (회귀)

    • 연속형 값을 예측

    • 예) 주가 예측

    • Mean squared error 를 loss function으로 사용

      • nn.MSELoss() loss function 사용

    • Loss(y^(i),y(i))=12(y^(i)−y(i))2\large Loss(\hat y^{(i)} ,y^{(i)}) = \frac 1 2 (\hat y^{(i)} - y^{(i)})^2

      y(i)y^{(i)}: 실제 값(Ground Truth), y^(i)\hat y^{(i)}: 모델이 예측한 값

  • API

    문제별 출력레이어 Activation 함수, Loss 함수

문제형태출력 Activation함수Loss 함수
이진분류(Binary Classification)sigmoidbinary crossentropy
다중분류(Multi-class Classification)softmaxcrossentropy
회귀(Regression)NoneMSE

문제별 출력레이어 Activation 함수, Loss 함수

문제형태출력 Activation함수Loss 함수
이진분류(Binary Classification)sigmoidbinary crossentropy
다중분류(Multi-class Classification)softmaxcrossentropy
회귀(Regression)NoneMSE

Optimizer (최적화 방법)

  • Training시 모델 네트워크의 parameter를 데이터에 맞춰 최적화 하는 알고리즘

    • Deep Learning은 경사하강법(Gradient Descent)와 오차 역전파(back propagation) 알고리즘을 기반으로 파라미터들을 최적화한다.

    Gradient Decent (경사하강법)

  • 최적화

    • 모델 네트워크가 출력한 결과와 실제값(Ground Truth)의 차이를 정의하는 함수를 Loss function(손실함수, 비용함수) 라고 한다.
    • Training 시 Loss function이 출력하는 값을 줄이기 위해 파라미터(weight, bias)를 update 과정을 최적화(Optimization) 이라고 한다.

  • Gradient Decent(경사하강법)

    • 최적화를 위해 파라미터들에 대한 Loss function의 Gradient값을 구해 Gradient의 반대 방향으로 일정크기 만큼 파라미터들을 업데이트 하는 것을 경사하강법이라고 한다.

Wnew=W−α∂∂WLoss(W)W:파라미터 α:학습률\large W_{new} = W-\alpha\frac{\partial}{\partial {W}}Loss(W)\\W: 파라미터\: \alpha:학습률

오차 역전파(Back Propagation)

  • 딥러닝 학습시 파라미터를 최적화 할 때 추론한 역방향으로 loss를 전달하여 단계적으로 파라미터들을 업데이트한다.

    • Loss에서부터(뒤에서부터) 한계단씩 미분해 gradient 값을 구하고 이를 Chain rule(연쇄법칙)에 의해 곱해가면서 파라미터를 최적화한다.
    • 출력에서 입력방향으로 계산하여 역전파(Back propagation)라고 한다.
      • 추론의 경우 입력에서 출력 방향으로 계산하며 이것은 순전파(Forward propagation)이라고 한다.

    계산 그래프 (Computational Graph)

  • 복잡한 계산 과정을 자료구조의 하나인 그래프로 표현한 것

    • 딥러닝 모델이 구현된 방식

  • 그래프는 노드(Node)와 엣지(Edge)로 구성됨.

    • 노드: 연산을 정의
    • 엣지: 데이터가 흘러가는 방향

  • Deep learning Network는 계산그래프로 구성된다

계산 그래프의 예

  • 슈퍼에서 1개에 100원인 사과를 2개 샀을 때 지불할 금액은 어떻게 될까? 단 부가세는 10% 부과된다.

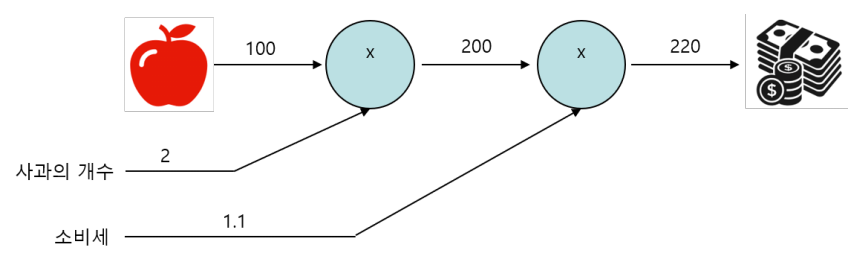
계산 그래프 절차 및 특장점

  • 계산 그래프를 사용한 문제 풀이 절차
    • 계산 그래프를 구성
    • 계산 방향을 결정
      • 계산 시작에서 계산 결과 방향으로 순서대로 계산: 순전파(Forward propagation)
      • 계산 결과에서 계산 시작 역방향으로 계산: 역전파(Back propagation)
  • 특징/장점
    • 국소적 계산을 통해 결과를 얻는다.
      • 각 노드의 계산은 자신과 관계된 정보(입력 값들)만 가지고 계산한 뒤 그 결과를 다음으로 출력한다.
    • 복잡한 계산을 단계적으로 나눠 처리하므로 문제를 단순하게 만들어 계산할 수 있다.
      • 딥러닝에서 역전파를 이용해 각 가중치 업데이트를 위한 미분(기울기) 계산을 효율적으로 할 수 있게 된다.
    • 중간 계산결과를 보관할 수 있다.

합성함수의 미분

  • 합성함수 : 여러 함수로 구성된 함수
    z=(x+y)2z=t2t=x+y\large z = (x+y)^2\\ \large z = t^2\\ \large t=x+y
  • 연쇄 법칙(Chain Rule)
    - 합성함수의 미분은 합성함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
    ∂z∂x=∂z∂t∂t∂x∂z∂t=2t,  ∂t∂x=1∂z∂x=2t×1=2(x+y)\large\cfrac{\partial z}{\partial x} = \cfrac{\partial z}{\partial t} \cfrac{\partial t}{\partial x} \\ \cfrac{\partial z}{\partial t} = 2t,\;\cfrac{\partial t}{\partial x} = 1 \\ \large\cfrac{\partial z}{\partial x}=2t \times 1 = 2(x+y)

연쇄 법칙과 계산 그래프

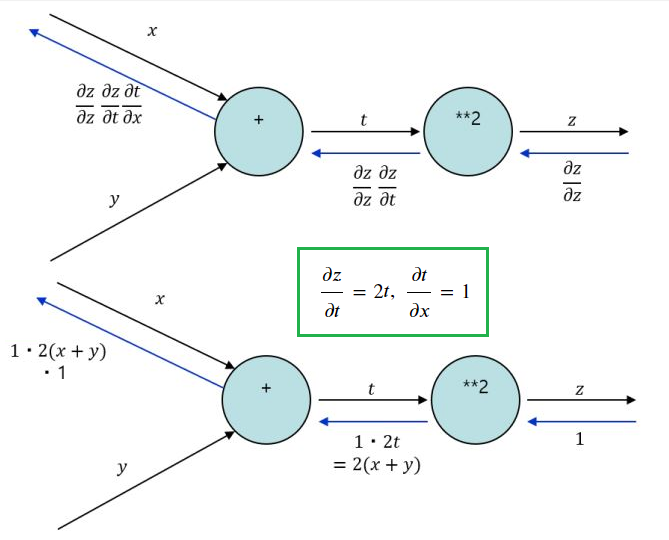
딥러닝 네트워크에서 최적화 예

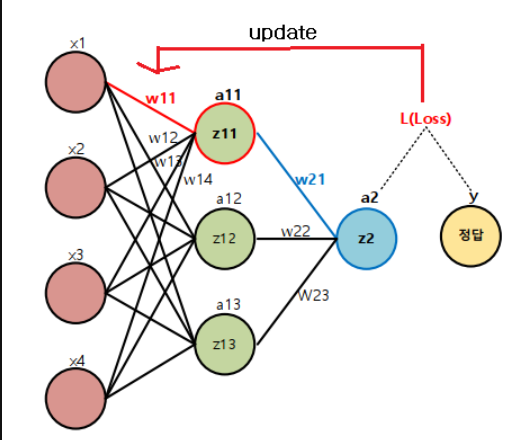
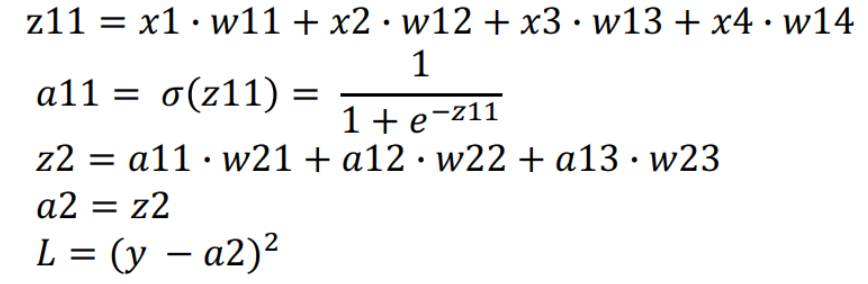
  • W11W_{11}을 업데이트 하기 위한 미분값은?

    ∂∂W11Loss=????\large\frac{\partial}{\partial {W_{11}}}{Loss} = ????

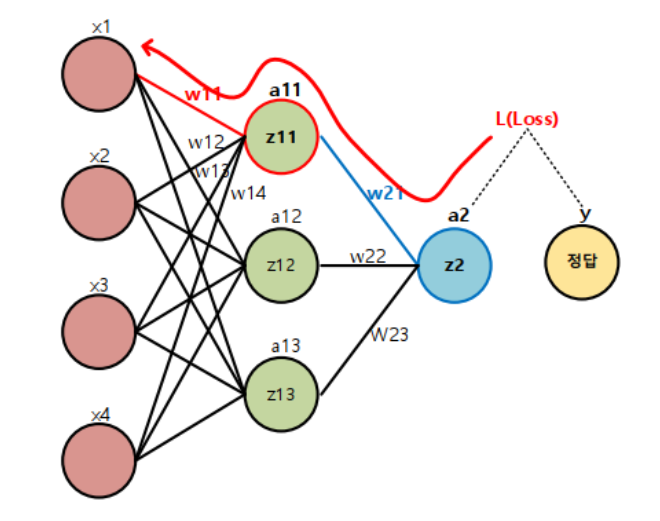
  • 순전파(forward propagation): 추론
  • 역전파(back propagation): 학습시 파라미터(weight) 업데이트

파라미터 업데이트 단위

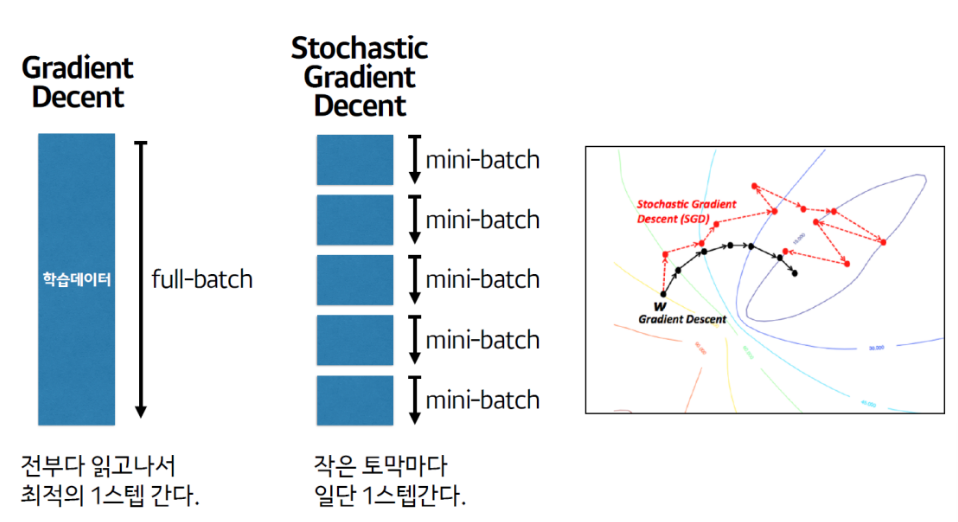
  • Batch Gradient Decent (배치 경사하강법)

    • Loss를 계산할 때 전체 학습데이터를 사용해 그 평균값을 기반으로 파라미터를 최적화한다.
    • 많은 계산량이 필요해서 속도가 느리다. 학습 데이터가 클 경우 메모리가 부족할 수 있다.

  • Mini Batch Stochastic Gradient Decent (미니배치 확률적 경사하강법)

    • Loss를 계산할 때 전체 데이터를 다 사용하지 않고 지정한 데이터 양(batch size) 만큼 마다 계산해 파라미터를 업데이트 한다.
    • 계산은 빠른 장점이 있지만 최적값을 찾아 가는 방향이 불안정 하여 부정확 하다. 그러나 반복 횟수를 늘리면 Batch 방식과 유사한 결과로 수렴한다.

스텝(Step): 한번 파라미터를 업데이트하는 단위

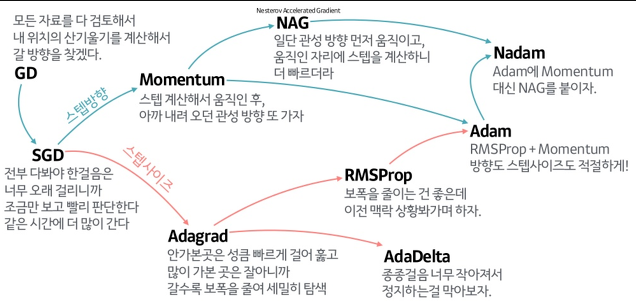
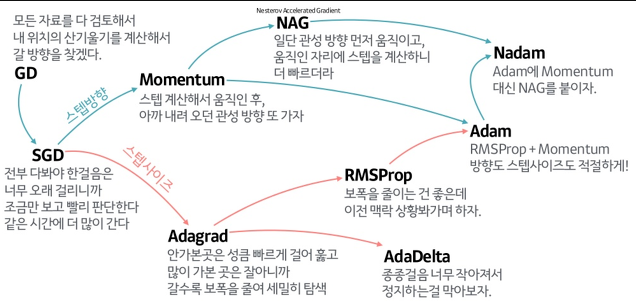
SGD를 기반으로 한 주요 옵티마이저

  • 방향성을 개선한 최적화 방법
    • Momentum
      • 학습률을 계산할 때 이전 step 까지의 gradient의 (누적)합을 더해서 계산한다.
  • 학습률을 개선한 최적화 방법
    • Adagrad
      • 파라미터 별로 다른 학습률을 계산한다. 각 파라미터의 학습률은 파라미터가 업데이트될 수록 반비례하여 작아지도록 계산한다.
        • 이전 기울기의 제곱들을 누적한 값의 제곱근의 역수를 학습율에 곱한다.
    • RMSProp
      • Adagrad는 학습이 진행될 수록 이전 기울기의 제곱들을 누적한 값이 커지므로 학습률이 점점 0에 수렴하는 문제가 있다.(학습율에 누적값의 역수를 곱하므로). RMSProp은 기울기를 단순 누적하지 않고 지수 가중 이동 평균 사용하여 최신 기울기들이 더 크게 반영하여 0에 수렴하는 문제를 해결함.
  • 방향성 + 학습률 개선 최적화 방법
    • Adam
      • Adagrad와 RMSProp을 합친 방식

[출처] https://www.slideshare.net/yongho/ss-79607172
profile
Bleu
이전 포스트

딥러닝 Deeplearning 4

다음 포스트

딥러닝 Deeplearning 6

0개의 댓글