딥러닝 Deeplearning 3

Bleu·2023년 10월 16일
notepython
0

python

목록 보기
19/22

모델링

모델 정의

  • Feature와 Target간의 관계를 수식으로 정의한다.
  • 여기서는 공부시간(Feature)와 점수(Target)간의 관계를 정의하는데 선형회귀(Linear Regression) 모델 을 가설로 세우고 모델링을 한다.
    • 많은 머신러닝 연구자들이 다양한 종류의 데이터에 관계를 예측할 수 있는 여러 알고리즘을 연구했다.
    • 선형회귀 모델은 입력데이터와 출력데이터가 선형관계(비례 또는 반비례 관계)일때 좋은 성능을 나타낸다.

가설

  • 아직은 이 식이 맞는지 틀린지는 알 수없기 때문에 이 식을 가설(hypothesis) 라고 한다.
  • 가설을 세우고 모델링을 한 뒤 검증을 해서 좋은 예측결과를 내면 그 가설을 최종 결과 모델로 결정한다. 예측결과가 좋지 않을 경우 새로운 가설로 모델링을 한다.

선형회귀 (Linear Regression)

  • Feature들의 가중합을 이용해 Target을 추정한다.
  • Feature에 곱해지는 가중치(weight)들은 각 Feature가 Target 얼마나 영향을 주는지 영향도가 된다.
    • 음수일 경우는 target값을 줄이고 양수일 경우는 target값을 늘린다.
    • 가중치가 0에 가까울 수록 target에 영향을 주지 않는 feature이고 0에서 멀수록 target에 많은 영향을 주는 target이 된다.
  • 모델 학습과정에서 가장 적절한 Feature의 가중치를 찾아야 한다.
y^=Wx+b\hat{y} = Wx + b
$\hat{y}$: 모델추정값
W: 가중치
x: Feature
b: bias(편향)

< 경사 하강법을 이용한 최적화>

예시 제시

(3-2 파일 보기)

최적화 (Optimize)

  • 모델을 학습하는 과정이 최적화 과정이다.

  • 모델의 예측값과 실제 값의 차이 즉 오차를 계산하는 함수를 만들고 그 오차를 가장 적게 만드는 파라미터를 찾는 작업을 한다.

    최적화 문제

  • 어떤 함수가 반환할 수 있는 가장 작은 또는 가장 큰 값을 반환하도록 하는 파라미터 값을 찾는 문제를 최적화 문제라고 한다.

  • 머신러닝은 Loss 함수(오차계산함수)가 반환하는 값(오차)를 최소화 할 수 있는 파라미터를 찾는 작업을 학습 과정에서 진행한다.
    - arg ->argument

wi=arg⁡min⁡wf(w)w_{i} = \arg \min_w f(w)
f(): 손실함수 w: 파라미터

손실함수(Loss Function), 비용함수(Cost Function), 목적함수(Object Function), 오차함수(Error Function)

  • 모델의 예측한 값과 정답값 간의 차이(오차)를 계산하는 함수.

  • 모델을 학습시키는 것은 이 함수의 반환값(Loss)을 최소화 하는 파라미터을 찾는 과정이다.

  • 문제 유형에 따라 Loss를 계산하는 방법이 다르다.

    • Classification(분류)의 경우 log loss(cross entropy)를 사용한다.
    • Regression(회귀)의 경우 MSE(Mean Squared Error)를 사용한다.

    최적화 문제를 해결하는 방법

  • Loss 함수 최적화 함수를 찾는다.

    • Loss를 최소화하는 weight들을 찾는 함수(공식)을 찾는다.
    • Feature와 sample 수가 많아 질 수록 계산량이 급증한다.
    • 최적화 함수가 없는 Loss함수도 있다.

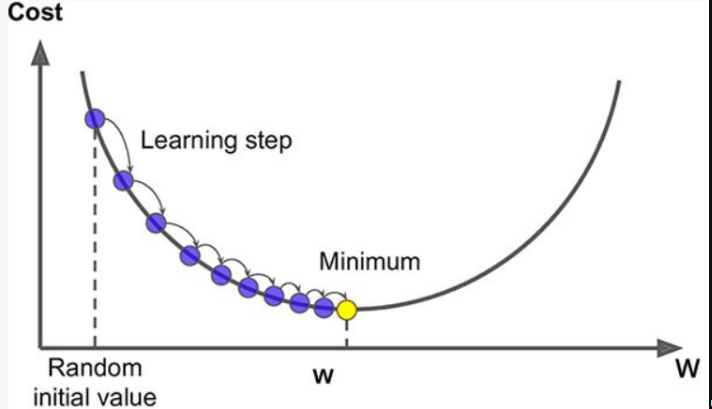
  • 경사하강법 (Gradient Descent)

    • 값을 조금씩 조금씩 조정해나가면서 최소값을 찾는다.

경사하강법 (Gradient Descent)

  • 다양한 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘. 특히 최적화 함수가 없는 모델의 경우 경사하강법을 사용한다.
  • 손실함수를 최소화하는 파라미터를 찾기위해 반복해서 조정해 나간다.
    1. 파라미터 WW에 대해 손실함수의 현재 gradient(경사,기울기,순간변화율)를 계산한다.
      • gradient는 파라미터에 대한 손실함수의 순간변화율 즉 미분해서 구한다.
    2. gradient가 감소하는 방향으로 파라미터 WW를 변경한다.
    3. gradient가 0이 될때 까지 반복 1,2 를 반복한다.
  • Gradient의 부호에 따른 새로운 파라미터값 계산
    • gradient가 양수이면 loss와 weight가 비례관계란 의미이므로 loss를 더 작게 하려면 weight가 작아져야 한다.
    • gradient가 음수이면 loss와 weight가 반비례관계란 의미이므로 loss를 더 작게 하려면 weight가 커져야 한다.

파라미터 조정

w가 변화하면 오차는 어떻게 바뀔까?
음수 > w가 작아지면 오차가 커짐

    > w가 커지면 오차가 작아짐

양수 > w가 작아지면 오차 작아짐

w가 커지면 오차가 커짐

Wnew=W−α∂∂Wcost(W)W_{new} = W-\alpha\frac{\partial}{\partial {W}}cost(W)
$W$: 파라미터
$\alpha$:학습률
  1. 현재 파라미터에 대해 Loss를 미분 한다.
  2. 1의 값에 Learning rate를 곱한 뒤 현재 파라미터값에서 뺀다.
  • 학습률 (Learning rate)
    • 기울기에 따라 이동할 step의 크기. 경사하강법 알고리즘에서 지정해야하는 하이퍼 파라미터이다.
    • 학습률을 너무 작게 잡으면 최소값에 수렴하기 위해 많은 반복을 진행해야해 시간이 오래걸린다.
    • 학습률을 너무 크게 잡으면 왔다 갔다 하다가 오히려 더 큰 값으로 발산하여 최소값에 수렴하지 못하게 된다.

다중 입력, 다중 출력

  • 다중입력: Feature가 여러개인 경우
  • 다중출력: Output 결과가 여러개인 경우

다음 가상 데이터를 이용해 사과와 오렌지 수확량을 예측하는 선형회귀 모델을 정의한다.
참조

온도(F)강수량(mm)습도(%)사과생산량(ton)오렌지생산량
7367435670
91886481101
8713458119133
10243372237
699670103119
사과수확량  = w11 * 온도 + w12 * 강수량 + w13 * 습도 + b1
오렌지수확량 = w21 * 온도 + w22 * 강수량 + w23 *습도 + b2
  • 온도, 강수량, 습도 값이 사과와, 오렌지 수확량에 어느정도 영향을 주는지 가중치를 찾는다.
    • 모델은 사과의 수확량, 오렌지의 수확량 두개의 예측결과를 출력해야 한다.
    • 사과에 대해 예측하기 위한 weight 3개와 오렌지에 대해 예측하기 위한 weight 3개 이렇게 두 묶음, 총 6개의 weight를 정의하고 학습을 통해 가장 적당한 값을 찾는다.
      • 이 묶음을 딥러닝에서는 Node, Unit, Neuron 이라고 한다.
  • 목적은 우리가 수집한 train 데이터셋을 이용해 정확한 예측을 위한 weight와 bias를 찾는 것이다.
profile
Bleu
이전 포스트

딥러닝 Deeplearning 2

다음 포스트

딥러닝 Deeplearning 4

0개의 댓글