그래서 메타 러닝이 어떻게 작동하는데? (논문 리뷰:Unraveling Meta-Learning)

밤🌰·2022년 9월 11일

논문 리뷰

목록 보기

1/1

안녕하세요, 밤🌰입니다.
이번에 리뷰할 논문은 Micah Goldblum et al.의 Unraveling Meta-Learning: Understanding Feature Representations for Few-Shot Tasks입니다.

바로 시작하겠습니다.

서문

메타 러닝은 퓨샷 분류 문제를 해결하기 위한 필수적인 방법입니다. 메타 러닝은 '학습하는 법을 학습한다' (learn-to-learn; l2l)라는 아이디어에서 출발했는데요, 지금껏 본 적 없던 데이터이더라도 그 데이터의 특성을 빠르게 학습할 수 있다면, 금방 적응 (adapt)할 수 있으리라는 것입니다.

따라서 메타 러닝에서 가장 유명한 Chelsea Finn의 MAML을 포함한 많은 메타 러닝 알고리즘이 그 방법을 모사하고 있습니다. 알고리즘을 학습하는 반복문과 학습하는 법을 학습하는 반복문으로 구성하는 것이죠. 따라서 많은 메타 러닝 알고리즘이 중첩 루프 (nested loop) 형태를 가집니다.

그러나 학습하는 법을 학습한다는 기조로 발전된 알고리즘이더라도, 실제로 학습하는 법을 학습한 것인지는 확인이 필요합니다. 수많은 메타 러닝 관련 논문이 세상에 나왔지만, 왜 메타 러닝이 잘 작동하는지 설명하는 논문은 잘 없습니다.

이 논문은 메타 러닝의 특징 추출 (feature extraction) 메커니즘을 더 파헤쳐 봄으로써 메타 러닝이 뽑아낸 특징이 왜 더 잘 작동하는지 알아보고자 했습니다. 다만, 이 논문 또한 이론적 근거를 제시하진 않기 때문에 결국 경험적 (empirical) 증명에 국한되어 있습니다.
이론적 근거를 찾는 것은 그 자체로 어려운 task이고, 선례도 없습니다. 그렇기에 이를 논문의 단점으로 뽑기엔 가혹할 수 있습니다. 또 논문은 '메타 러닝 feature의 특징'을 보이는 데엔 성공했습니다. 그러나, 그 특징과 실험을 연결 짓는 논리는 부족해 보입니다. 저자들도 이를 인지하고 있기 때문에 결론에 '메타 러닝이 왜 더 잘 작동하는지 밝혀냈다'고 적지 않습니다.

그럼에도 이 논문은 다양한 메타 러닝 알고리즘과 그 알고리즘이 추출한 feature를 이해하는 데에 굉장히 도움이 됩니다. 원문을 읽어보시는 것을 추천해 드립니다.

자세한 내용은 아래에서 계속하겠습니다.

요약

고전적 학습 방식과 메타 러닝이 추출한 feature가 본질적으로 어떻게 다른지 알아봅니다. (고전적 방식은 메타 러닝이 아닌 다른 일반적인 학습 알고리즘을 칭합니다.)

저자는 메타 러닝 알고리즘을 Inner-Loop 실행 중에 feature extractor를 고정하는 모델과 고정하지 않는 모델로 나눕니다. Feature extractor의 고정 여부에 따라 추출되는 feature가 다를 테니, 따로따로 분석하고자 한 것이죠. 각각의 경우에서 feature embedding의 특징을 확인해보고, 그 특징을 반영하는 regularizer를 만듭니다. 그 regularizer를 일반 알고리즘에 적용해보고 성능 향상이 있는지 확인해봅니다. 성능 향상이 있다면, 메타 러닝을 통해 얻는 그 특징이 메타 러닝의 성능 향상을 불러왔을 것이라고 예상할 수 있습니다.

저자가 각 방식에 대해 내린 결론은 다음과 같습니다.

Inner-Loop 중에 feature extractor가 고정된 모델 (MetaOptNet과 R2-D2)은 feature embedding이 고전적 방식과 비교해 유의미한 차이가 있다.
- 메타 러닝 모델의 feature가 feature space에서 더 잘 cluster 되는 것을 확인할 수 있었다.
  - 잘 cluster 된다는 것은 같은 클래스끼리 모이고, 다른 클래스끼리 떨어진다는 것.
- 더 잘 cluster 되도록 regularizer를 고전적 학습법에 적용해봤더니 성능 향상이 있었다.
Feature extractor가 고정되지 않은 모델 (Reptile)은 다양한 Task의 minima에 전체적으로 가까운 파라미터를 찾기 때문에 성능이 더 좋다.
- Reptile과 consensus optimization이 상당히 연관되어 있기 때문에 위와 같은 가설을 세울 수 있었다.
  - Reptile에 consensus optimization이 암시적으로 적용되어 있다고 본다.
- Reptile을 변형해 consensus optimization을 명시적으로 적용해주었더니 성능 향상이 있었다.

더 자세히 설명해보겠습니다.

메타 러닝 알고리즘의 분류

저자가 메타 러닝 알고리즘을 두 가지로 분류했다고 말했죠? Inner-Loop 도중 feature extractor의 고정 여부에 따라 나눴습니다.

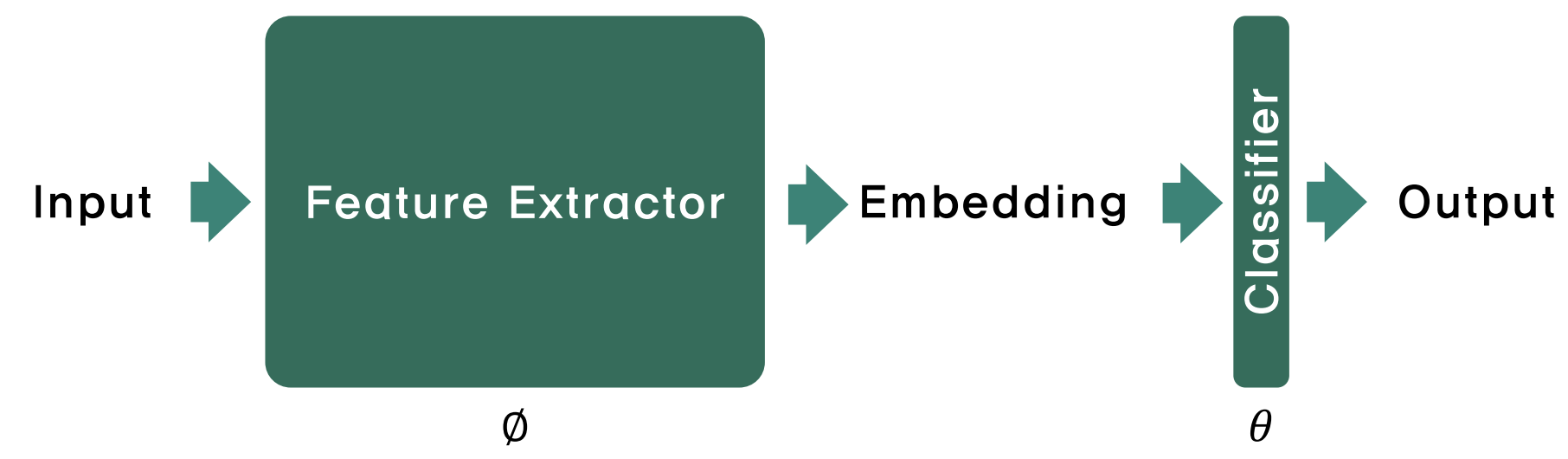
분류 알고리즘은 위와 같이 feature extractor와 마지막 classifier 층으로 나누어 볼 수 있습니다. 입력을 feature extractor 층을 통해 매핑(사상)시킨 뒤, 그 결과를 분류기 층을 이용해 분류하는 것입니다.

메타 러닝에서 inner-loop는 fine-tuning을 뜻합니다.
Inner-loop 중에 feature-extractor를 고정한다는 것은, fine-tuning 중에 embedding이 변화하지 않는다는 것입니다. 이로써 더 나은 feature extractor를 학습하는 것은 오로지 outer-loop의 몫이 됩니다. (Outer-loop는 흔히 meta-update이라고 말합니다. 메타 학습을 통한 파라미터 업데이트를 지칭하는 것이지요.)

(Inner-loop 중에 feature extractor가 고정된 모델에는 ProtoNet, MetaOptNet과 R2-D2가 있습니다.)

반대로, inner-loop 중에 feature extractor가 고정되지 않는 모델은 feature extractor의 파라미터도 같이 업데이트 되겠죠? Fine-tuning 중에도 더 나은 embedding을 학습할 기회가 있는 것입니다.
(고정되지 않는 모델엔 Reptile이 있습니다.)

그러면 각 방법으로 추출된 feature가 어떤 모습을 보이는지 확인해봅시다.

각 방법의 feature

고정된 모델

첫 번째론 inner-loop 중에 feature extractor가 고정된 모델입니다. 위에서 말씀드렸듯, feature extractor가 고정되었기 때문에, fine-tuning 시엔 더 나은 feature를 학습할 기회가 없습니다. 이전 단계 (iteration)의 outer-loop에서 feature를 잘 추출해냈어야 하는 것이죠.
예시와 함께 설명하겠습니다.

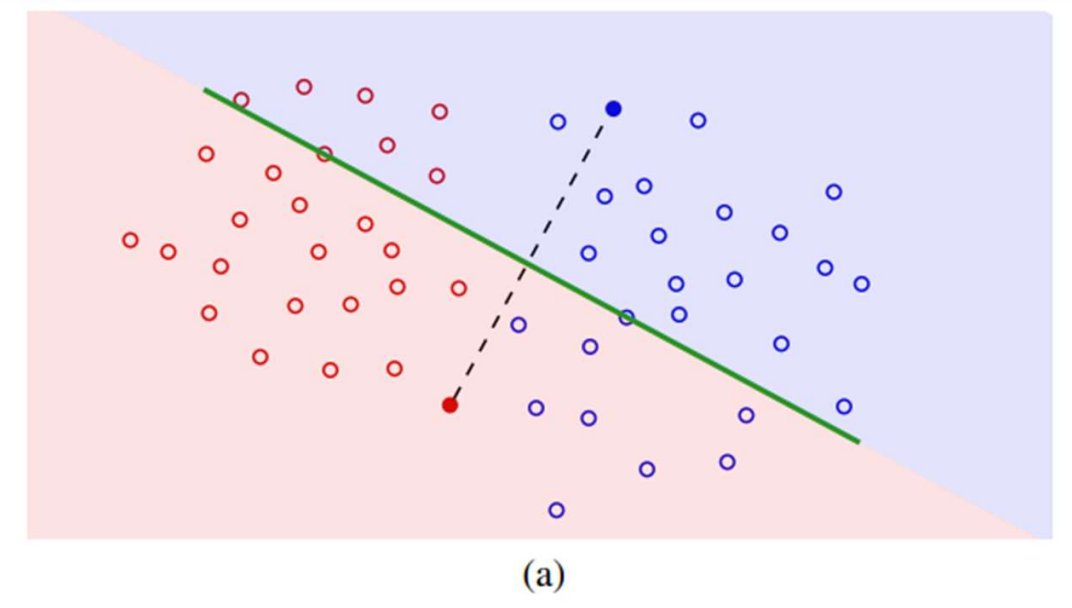
빨간색과 파란색 점이 Embedding을 뜻합니다. Feature extractor를 학습한다는 것은 이 점들이 '잘' 분포하도록 학습한다는 것을 뜻합니다.
초록색 선은 classifier입니다. 선을 기준으로 한쪽은 빨간색, 한쪽은 파란색으로 분류하고 있는 것이 보이죠? 잘 분류하고 있는 것 같지는 않네요. (초록색 선은 2D에선 선, 3D에선 평면이 되겠죠? 이러한 것을 hyperplane, 초평면이라고 합니다.)

Fine-tuning 시에 classifier만 업데이트한다는 것은 곧 초록색 선만 새로 긋는다는 것을 말합니다. 빨간색, 파란색 점은 그대로 둔 채요.

그렇다면 좋은 embedding은 뭘까요? 초록색 선을 잘 그을 확률을 높이는 embedding입니다. (논문에 직접적으로 확률이라는 단어가 언급되어 있지 않습니다. 이해를 위해 추가했습니다.)
위 사진에서 보시면, feature embedding 자체는 잘 분리가 되어있습니다. 두 class를 완벽히 분리하는 직선을 찾을 수 있습니다. 다만, 찾기가 힘듭니다. 모든 데이터를 보지 못하기 때문에 (퓨샷 분류이기에 더더욱 그렇습니다.) 샘플링에 크게 종속된다는 문제가 있죠. 위 사진이 바로 그 경우입니다. 빨간색, 파란색으로 채워진 점이 샘플된 데이터입니다. 샘플된 데이터를 기준으로 초평면을 그렸는데, 완전히 실패한 분류기가 되었습니다. 이게 논문에서 말하는 "선형 분리가 가능한 (linearly separable) 것이 좋은 분류기의 충분조건이 아닌" 이유입니다.

좋은 embedding은 아래와 같이 나타납니다.

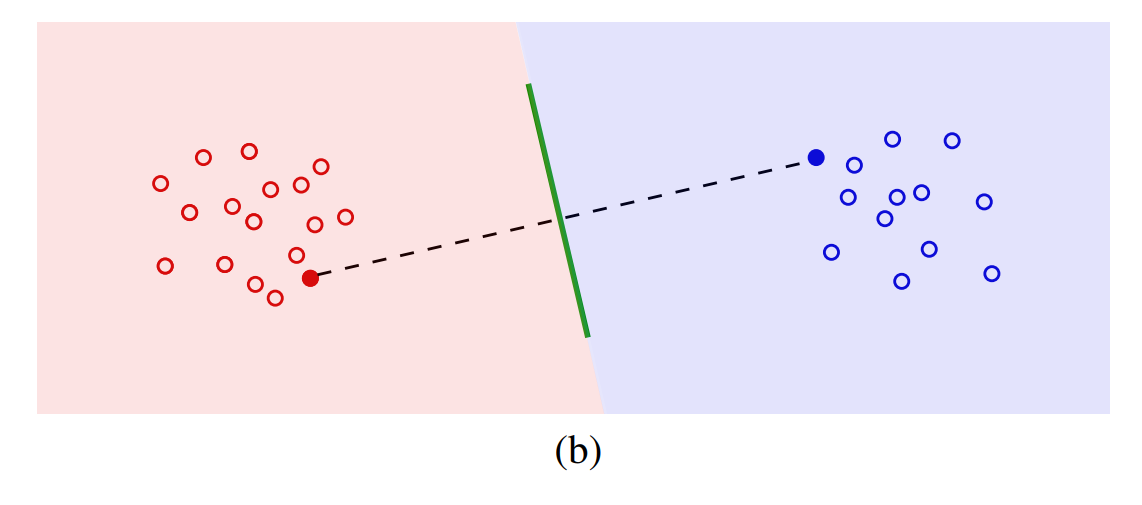
어떤 샘플을 뽑더라도 classifier가 두 class를 잘 분류하겠죠?

다시 메타 러닝으로 돌아옵시다.
메타 러닝이 좋은 임베딩을 학습할 것이라는 건 (b)와 같은 임베딩을 학습할 것이라고 예상하는 것입니다. (b)와 같은 임베딩이라고 한다면,

클래스 간의 거리가 멀고,
클래스 내 샘플 간의 거리가 가까운

임베딩을 뜻합니다. 자기들끼리 모여있는 임베딩이라고 할 수 있겠네요.

이해되나요? 다른 색끼리는 멀고, 같은 색끼리는 가까운 임베딩입니다.

논문은 이를 class clustering이라고 부릅니다.
Class clustering을 점수화해서 메타 러닝과 고전적 알고리즘에서 각각 측정해본다면, 메타 러닝이 좋은 feature embedding을 학습하는지 직접 확인이 가능할 것입니다. 밑에서 보여드릴 것이지만, 스포하자면 메타 러닝이 더 좋은 embedding을 가집니다. (당연함. 논문이 나왔음.)
마지막으로 이 점수를 이용해 기존 알고리즘을 향상해 봅시다.

고정하지 않은 모델

(논문에서는 reptile 알고리즘만을 예시로 설명하고 있습니다.)
Reptile은 Alex Nichol 등의 On First-Order Meta-Learning Algorithms라는 논문에서 소개된 알고리즘입니다.
제목에서 보이듯, MAML에서 2차 미분을 제거한 알고리즘입니다. 기존에 FOMAML이 있었고, 이를 보완해 Reptile이 나오게 되었습니다.

Reptile은 fine-tuning을 통해 빠르게 태스크별 최적점 (task-specific minimum)에 도달할 수 있습니다. 하지만 2차 미분을 하지 않는 reptile은 loss landscape의 정보가 부족할 텐데, 빠르게 최적점에 도달할 수 있는 이유가 무엇일까요?

저자들이 예측하기를, 이는 애초에 파라미터가 많은 태스크의 최적점들(minima)에 가깝도록 학습되었기 때문일 것입니다.

저자의 예측에는 근거가 하나 더 있습니다.
바로 Reptile과 consensus optimization의 연관성인데요. Reptile은 아래에 보이는 consensus formulation이라는 것을 최소화하는 것으로 볼 수도 있다고 합니다.

\frac 1 m \sum^m _{p=1}\mathcal L _{\mathcal T_p}(\tilde \theta _p) + \frac \gamma 2 \| \tilde \theta_p - \theta \|^2

이는 consensus optimization과 같습니다. 뒤에 붙은 페널티 항이 태스크별 파라미터 $\tilde \theta _p$ 로 하여금 Consensus value라는 값 ( $\theta$ ) 근처에 머물러 있도록 합니다. Task 전반의 minima를 consensus value로 둔다면 우리가 reptile에 세운 가정과 같아지는 것을 볼 수 있죠. 하지만 reptile은 저 뒤에 더해져 있는 페널티 항이 암시적으로만 (implicitly) 반영되어 있습니다.
이 사실을 이용해 기존의 알고리즘을 향상해 봅시다.

실험과 결과

고정한 모델

클래스 간 거리와 클래스 내 샘플 간 거리를 다음과 같이 점수화합니다.

R_{FC}(\theta, \{x_{i,j}\} = { c \over N } \frac {\sum_{i,j} \| f_\theta (x_{i,j}) - \mu_i \|^2_2}{\sum_i \| \mu_i - \mu \|^2_2}

$i$ 는 클래스 $i$ , $x_{i,j}$ 는 클래스 $i$ 의 $j$ 번째 data를 뜻합니다. $\mu_i$ 는 클래스 $i$ 의 평균, $\mu$ 는 모든 데이터의 평균을 뜻하죠. 그럼 이 regularizer가 무슨 뜻일까요? 분자는 클래스 내 샘플 간 거리, 분모는 클래스 간 거리를 뜻함을 알 수 있습니다. 즉, 클래스 내 샘플들끼리 가까워질수록, 클래스끼리 멀어질수록 $R_{FC}$ 는 작아질 것입니다.
이걸 그대로 regularizer로 활용한다면, class clustering을 더 잘 할 수 있지 않을까요?

(논문에선 이와 별개로 $R_{HV}$ 라는 수치도 도입해 테스트합니다. $R_{FC}$ 와 아이디어는 비슷하고, 방법이 조금 다릅니다. 없어도 논문의 메인 아이디어를 이해하는 데에 문제가 없기 때문에 생략합니다.)

Regularizer를 고전적 알고리즘에 적용한 결과는 다음과 같습니다.

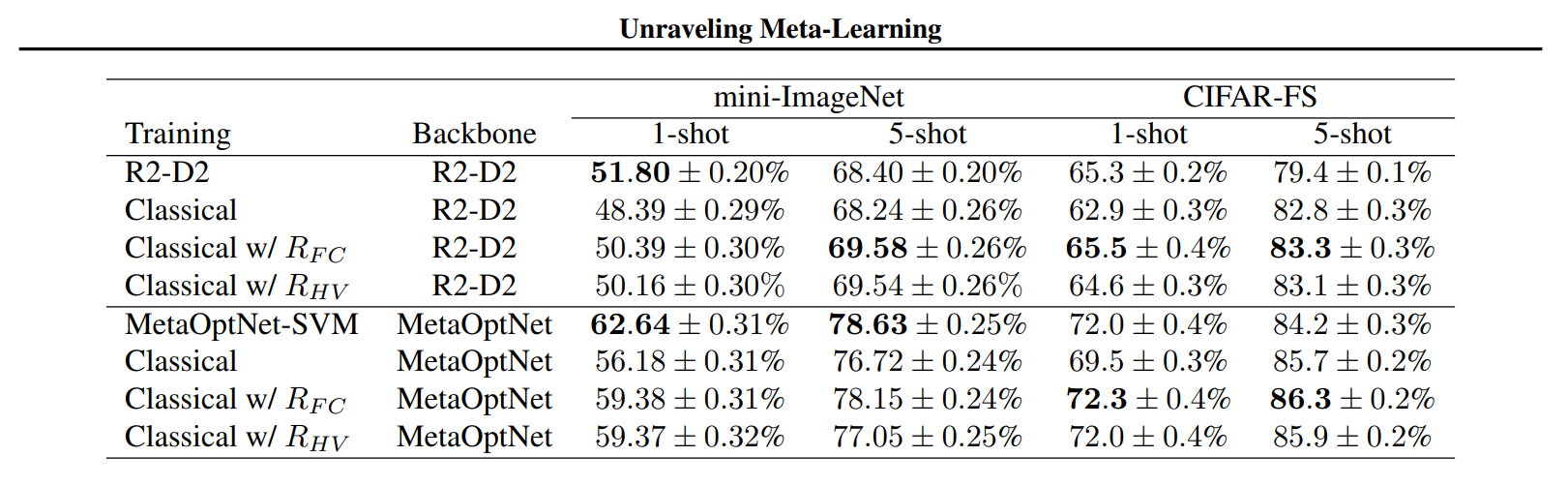
메타 러닝이 갖는 특징이 곧 '잘 clustering 된다'이고, 잘 clustering 되도록 하면 성능이 좋아짐을 볼 수 있습니다.

고정하지 않은 모델 (Reptile)

\frac 1 m \sum^m _{p=1}\mathcal L _{\mathcal T_p}(\tilde \theta _p) + \frac \gamma 2 \| \tilde \theta_p - \theta \|^2

여기서 암시적으로 적용되었던 항인 ${\gamma \over 2} \| \tilde \theta_p - \theta \|^2$ 을 reptile에 명시적으로 적용해봅니다. 성능향상이 있을까요?
이번에 적용할 regularizer는 다음과 같습니다.

R_i\left(\left\{\tilde{\theta}_p\right\}_{p=1}^m\right)=d\left(\tilde{\theta}_i, \frac{1}{m} \sum_{p=1}^m \tilde{\theta}_p\right)^2

파라미터의 평균과 파라미터 간의 거리를 regularizer로 사용했습니다. Feature가 아닌 파라미터들이 cluster 되도록 하는 것이죠. 따라서 이를 weight clustering이라고 부릅니다. Weight clustering을 reptile에 적용한 결과는 아래와 같습니다.

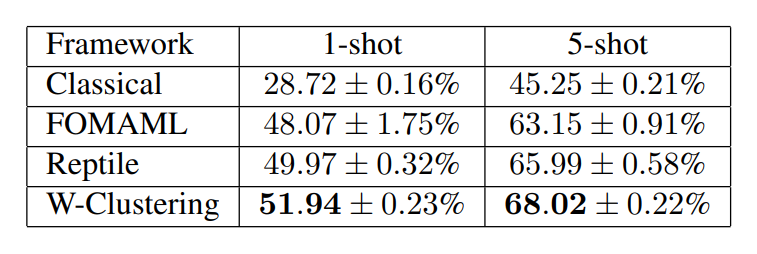
결론

메타 러닝과 고전적 알고리즘이 어떻게 다른지를 보였습니다. 논문은 결론을 '메타 러닝이 우수하다'고 짓지 않습니다.

첫째, 메타 러닝이 $R_{FC}$ 를 최소화하는 방향으로 학습된다는 증거를 찾았고, 이 점에서 착안한 regularizer를 적용해 보았더니 성능을 높일 수 있었다. 따라서 클래스 내 feature variance를 최소화하는 것이 퓨샷 성능을 높이는 것에 critical 함을 알 수 있다.
둘째, reptile이 consensus optimization과 닮아있고, 이에 착안한 regularizer는 reptile의 성능을 높였다.

이상이 논문의 결론입니다.

'메타 러닝이 다른 알고리즘보다 뛰어난 이유' 등등보다는 메타 러닝의 feature가 갖는 특징 정도를 결론으로 얻어가는 게 좋아 보입니다.

사담

첫 글이라 힘들었습니다. 기존에 정리해 둔 내용이기 때문에 반나절 정도 소요해 작성할 생각이었는데, 어림도 없었네요. 자꾸 하고 싶은 말이 많아져서 내용이 길어지고, 또 그래서 횡설수설한 부분이 있는 것 같습니다. 좀 더 시간을 두고 적어야겠습니다.

밤🌰

안녕하세요, 메타 러닝을 공부하고 있습니다.

1개의 댓글

도리

2022년 9월 14일

유용한 포스팅 감사합니다

답글 달기