[Swift] [78일차] 2016_LEETCODE

2016. Maximum Difference Between Increasing Elements

---

문제 설명

1. [Int] 가 주어진다.
2. 여기에서 0<=i<j 인 nums[i]<nums[j] 의 가장 큰 차이를 구하라
3. 배열이 주어진 순서대로 존재하면서 숫자가 늘어나는 것을 파악해서 가장 큰 차이값 return

---

문제 풀이

class Solution {
    func maximumDifference(_ nums: [Int]) -> Int {
        var answer = [Int]()
        for i in 0 ..< nums.count - 1 {
            var temp = (min: nums[i], max: -1)
            for j in i + 1 ..< nums.count {
                if temp.min < nums[j] && temp.max < nums[j] { // 이거는 우상향 -> 오케이
                    temp.max = nums[j]
                }
            }
            answer.append(temp.max - temp.min)
        }

        return answer.max() ?? -1
    }
}

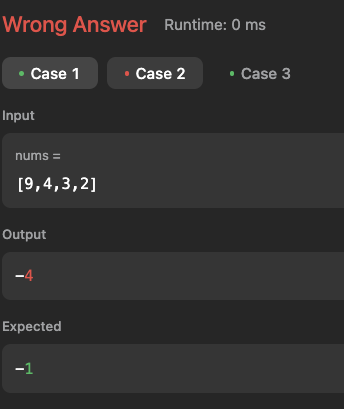
잘된줄 알았는데, 다음과 같이 오류가 있었다. [9,4,3,2]면 자연스럽게, -1이 나와야하는데(이게 우하향 배열이니까) 그렇지 않았다.

 answer.append(temp.max - temp.min)

모든 경우에서 다음과같이 temp.max - temp.min을 해주다보니, temp.max는 개선되지 않았음에도 계속헤서 answer에 값을 채워버린 것

그래서 조건을 부여해줬다.

if temp.max != -1 {
                answer.append(temp.max - temp.min)
            }

최종 제출 코드

class Solution {
    func maximumDifference(_ nums: [Int]) -> Int {
        var answer = [Int]()
        for i in 0 ..< nums.count - 1 {
            var temp = (min: nums[i], max: -1)
            for j in i + 1 ..< nums.count {
                if temp.min < nums[j] && temp.max < nums[j] { // 이거는 우상향 -> 오케이
                    temp.max = nums[j]
                }
            }
            if temp.max != -1 {
                answer.append(temp.max - temp.min)
            }
        }

        return answer.max() ?? -1
    }
}

---

타인의 코드

내 코드는 o(N^2)으로 풀리다보니, 좀 더 개선된 코드가 있지않을까 기대하면서 다른 코드를 살펴보았다.

class Solution {
    func maximumDifference(_ nums: [Int]) -> Int {
        // Initialize the minimum value with the first element
        var minVal = nums[0]
        // Initialize the maximum difference with -1
        var maxDiff = -1
        
        // Iterate through the array starting from the second element
        for i in 1..<nums.count {
            // If the current element is greater than the minimum value,
            // calculate the difference and update maxDiff if needed
            if nums[i] > minVal {
                maxDiff = max(maxDiff, nums[i] - minVal)
            } else {
                // Update the minimum value if the current element is smaller
                minVal = nums[i]
            }
        }
        
        // Return the maximum difference found or -1 if no valid difference
        return maxDiff
    }
}

O(N)으로 잘 풀어준 걸 확인할 수 있다.
minVal을 첫항으로 가지고가면서 예를들어 [1,5,2,10] 이 주어졌을때
1. minVal = 1
2. nums[i] = 5 , maxDiff = max(-1,4) -> maxDiff = 4
3. nums[i] = 2 , 여전히 nums[i] > minVal(1) 이므로 ,maxDiff = max(4,2-1)
4. nums[i] = 10 , maxDiff = max(4,10-1)
한 번에돌면서 해결을 해줄 수 있다. 이게 증가하는 부분수열 관련문제니까 관련 문제를 다음에 풀면서 익혀보도록 해야겠다.