[Swift] [48일차] 2120_LEET

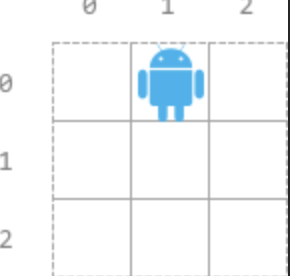
2120. Execution of All Suffix Instructions Staying in a Grid

---

문제 설명

1. 현재 위치에서 각 명령별로 [i]인덱스부터 실행가능한 명령 개수를 return

2. 나는 계속 누적되는 위치로서 이를 시행하는지알았는데 계속해서 startPos에서 시작이여서 엄청나게 쓸데없이 많은 리소르르 투자했던 것 같다. 그래서 inout으로 선언도 해주고, 각자 판단 로직을 함수로 짜주고 나서야 알았다..

func isRange(_ pos: [Int], _ n: Int) -> Bool {
    if pos[0] < 0 || pos[0] >= n || pos[1] < 0 || pos[1] >= n { // 적용범위안에 안될대
        return false
    }
    return true
}

func move(
    _ pos: inout [Int],
    _ direction: Character,
    _ n: Int
) -> Bool {
    let directions: [Character: (Int, Int)] = [
        "L": (0, -1),
        "R": (0, 1),
        "U": (-1, 0),
        "D": (1, 0),
    ]
    let (dx, dy) = directions[direction]!

    pos[0] += dx
    pos[1] += dy

    if isRange(pos, n) {
        return true
    }
    else {
        pos[0] -= dx
        pos[1] -= dy
        return false
    }
}

그래서 뭐 짯던거를 재활용하자면...!
1. 각 명령어에 따라 움직여주고, 못움직이는 상태면(맵을 벗어난다면 return false를 하고 움직인 좌표를 원상복구 시킨다.
2. 명령어를 쭉실행시키고, 앞에서하나를 짤라주고, 짜른 나머지 배열로서 이제 수행하고 카운팅하고를 반복했다.

제출코드

func isRange(_ pos: [Int], _ n: Int) -> Bool {
    if pos[0] < 0 || pos[0] >= n || pos[1] < 0 || pos[1] >= n { // 적용범위안에 안될대
        return false
    }
    return true
}

func move(
    _ pos: inout [Int],
    _ direction: Character,
    _ n: Int
) -> Bool {
    let directions: [Character: (Int, Int)] = [
        "L": (0, -1),
        "R": (0, 1),
        "U": (-1, 0),
        "D": (1, 0),
    ]
    let (dx, dy) = directions[direction]!

    pos[0] += dx
    pos[1] += dy

    if isRange(pos, n) {
        return true
    }
    else {
        pos[0] -= dx
        pos[1] -= dy
        return false
    }
}

class Solution {
    func executeInstructions(_ n: Int, _ startPos: [Int], _ s: String) -> [Int] {
        var s = ["L"] + Array(s)
        var answer = [Int]()

        repeat {
            var curr_pos = startPos
            var count = 0

            for (idx, command) in s.enumerated() {
                if move(&curr_pos, command, n) {
                    count += 1
                }
                else {
                    break
                }
            }
            answer.append(count)
            s.removeFirst()
        }
        while !s.isEmpty

        return answer
    }
}

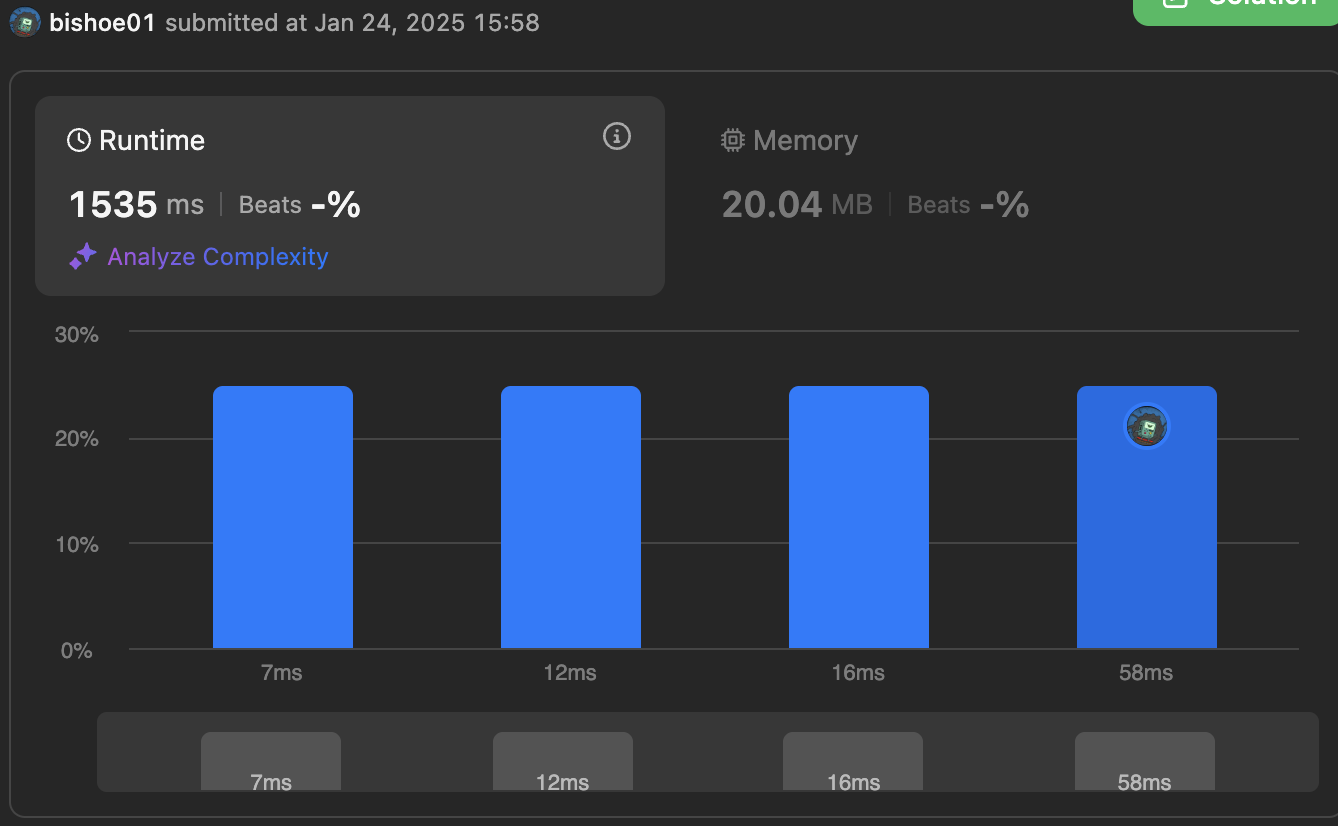보시다 시피 내 코드는 엄청나게 느려서 퍼센테이지도 안나왔다. O(N)으로 나름 머리굴려서 한건데, 접근방식이 좀 다른가 ?

타인의 코드

class Solution {
    func executeInstructions(_ n: Int, _ startPos: [Int], _ s: String) -> [Int] {
        let size = s.count
        var changes : [(Int, Int)] = Array(repeating: (0,0), count: size+1)
        changes[size] = (0,0) 

        var sArr = Array(s)

        for i in stride(from: size-1, through: 0, by: -1) {
            var newChange = (0,0)
            switch sArr[i] {
                case "L":
                    newChange = (0,-1) 
                case "R":
                    newChange = (0,1)  
                case "D":
                    newChange = (1,0)  
                case "U":
                    newChange = (-1,0) 
                default:
                    newChange = (0,0)
            }
            changes[i] = (changes[i+1].0 + newChange.0, changes[i+1].1 + newChange.1)
        }

        var results = Array(repeating: 0, count: size)

        for i in 0..<size {
            var countInst = 0
            for j in i..<size {
                // Compute the net movement from i to j-th instruction
                let deltaRow = changes[i].0 - changes[j+1].0
                let deltaCol = changes[i].1 - changes[j+1].1
                let newRow = startPos[0] + deltaRow
                let newCol = startPos[1] + deltaCol

                // Check if still inside the grid
                if newRow < 0 || newRow >= n || newCol < 0 || newCol >= n {
                    break
                }
                countInst += 1
            }
            results[i] = countInst
        }

        return results
    }
}

코드를 보면 알 수 있듯이 나는 정직하게 startPos부터 이동을 해보면서 판단을 해줬는데, 이게 보니까 changes라는 배열을 활용해서 이동량 자체를 배열로 만들어준 것을 볼 수 있다.
그래서 그 배열에 해당하는 만큼 이동할 수 있으면 가능한거니까.. 그래서 역순으로 배열을 순회하면서 이를 충족하게끔 해줬다.

마지막 명령이후로는 안움직이니까 changes[size] = (0, 0)

만약 s = "RRDD"가 주어졌을 때
R: (0, 1) 오른쪽으로 1칸
R: (0, 1) 오른쪽으로 1칸
D: (1, 0) 아래로 1칸
D: (1, 0) 아래로 1칸

이는 결국 시작점이랑 상관없이 다음과 같이 변화량 배열을 만들어낼 수 있다.

changes = [(2, 2), (2, 1), (2, 0), (1, 0), (0, 0)]

1. changes[0] = (2, 2)
2. changes[1] = (2, 1)
3. changes[2] = (2, 0)
4. changes[3] = (1, 0)
5. changes[4] = (0, 0)

이걸 이제 순환 시키면서 되는지만 판단해주면 될 것이다.
순환하면서

let deltaRow = changes[i].0 - changes[j+1].0
let deltaCol = changes[i].1 - changes[j+1].1
let newRow = startPos[0] + deltaRow
let newCol = startPos[1] + deltaCol

여기 이렇게 1번 명령부터보고 있으면 인접한 변화량 배열을 빼주면 현재 변호량이 ㄴ오는 것을 이용했ㄷ.